nierówności logarytmowe
diks: nierówności logarytmowe..
19 lis 12:38
diks: log2(x−1)>2
19 lis 12:38
diks: noi jak tu postępuje Aniu?

19 lis 12:38
aniabb: tak samo jak w równaniach

najpierw dziedzina
potem że log
pa > b to a>p
b o ile p>1 jak mniejsze to zmiana znaku na przeciwny
19 lis 12:40
diks: x−1>2
x>3
dziedzina (3,+∞)
19 lis 12:41
diks: (x−1)>22
(x−1)>4
x>5
19 lis 12:42
diks: x∊(5,+∞)
19 lis 12:42
diks: a to nawet wporządku te nierówności

19 lis 12:43
diks: następny log3(2−x)≤ 1
19 lis 12:43
diks: 2−x≤ 1
−x≤ −1 /*(−1)
x≥1
dziedzina x∊<1,+∞)
19 lis 12:44
diks: (2−x)>31
2−x>3
−x>1 /*(−1)
x<1
19 lis 12:46
diks: x<−1
19 lis 12:46
diks: coś ,mi nie wyszło bo odpowiedź to x∊<−1,2)
19 lis 12:47
19 lis 12:47
aniabb: w drugim to samo...a tak krytykowali że bez sensu piszesz warunki..widać wciąż musisz

19 lis 12:48
diks: w pierwszym dziedzina (3,+∞)
w drugim dziedzina x∊<1,+∞)
19 lis 12:48
diks: założenia? a>0, a≠1, b>0

19 lis 12:49
diks: a no tak już wiem..
19 lis 12:49
diks: x−1>0
x>1
dziedzina w pierwszym x∊(1,+∞)
19 lis 12:50
diks: 2−x>0
−x>−2 /*(−1)
x<2
19 lis 12:50
aniabb: teraz OK

19 lis 12:51
diks: ale w drugim mi wyszło, że x<−1 i dziedzina x<2
to chyba nie pasuje do tego? x∊<−1,2)
19 lis 12:52
diks: 2 mi pasuje.. ale −1 nie pasuje

19 lis 12:54
diks: no bo przecież x wyszło że jest mniejsze od −1
19 lis 12:54
aniabb: zrób jeszcze raz ładnie drugi bo zmieniłeś całkiem znak nierówności
19 lis 12:58
diks: (2−x)>31 2−x>3 −x>1 /*(−1) x<1
no dałem taki jaki podałaś mi wzór.. a to mam dostosować wzór do znaku? czyli dać taki znak jak
w nierówności mam konkretnej?
19 lis 12:59
diks: (2−x)≤31
2−x≤3
−x>≤1 /*(−1)
x≥−1
19 lis 12:59
diks: aa no i teraz pasuje

!
19 lis 12:59
diks: KOLEJNY log1/2 (2x+5) > 03
19 lis 13:00
diks: log1/2 (2x+5) > −3
19 lis 13:00
Aga1.: Licz.
19 lis 13:08
19 lis 13:08
diks: licze

19 lis 13:08
aniabb: no oczywiście znak że taki jak w treści zadania <umm>
19 lis 13:09
diks: x>2,5
zatem dziedzina to
(2,5,+∞)
19 lis 13:09
aniabb: przypominam że jak podstawa ułamkowa to zmieniamy znak
19 lis 13:10
aniabb: dziedzina OK

19 lis 13:10
diks: (2x+5)> (1/2)
−3
(2x+5)> 2
3
(2x+5)> 8
2x>3 /:2
19 lis 13:11
diks: który znak zmieniamy

?
19 lis 13:11
diks: x>1,5
19 lis 13:12
Eta:
Zmieniamy nie "znak" .......... tylko
zwrot nierówności

19 lis 13:13
diks: aha

zatem będzie x<1,5?

19 lis 13:14
aniabb: logpa >b to a <pb gdy 0<p<1
19 lis 13:14
Piotr:
ciekawe czy tu tez bedzie ponad 2,5 tys postow

19 lis 13:24
aniabb: zależy ile ma tych nierówności

19 lis 13:25
diks: nierówności jest trochę więcej od równości

19 lis 13:27
Kejt: to może to jakoś podziel..? bo naprawdę choćbym bardzo chciała Ci czasem pomóc to się w tych 2
tysiącach postów nie doszukam problemu..
19 lis 13:28
Piotr:

19 lis 13:28
aniabb: ale on ma większą wprawę i nie będzie ich rozpisywał co krok to post

19 lis 13:30
diks: teraz już może będzie trochę lżej.. po tych równaniach

19 lis 13:31
Piotr:
no oby

19 lis 13:32
diks: dobra czyli wyszła mi dziedzina (2,5,+∞) i x<1,5
19 lis 13:32
diks: więc moje x nie należy do dziedziny?
19 lis 13:32
aniabb: a nie..dziedzina była od − 5/2
19 lis 13:33
diks: aha czyli x>−2,5
19 lis 13:35
diks: (−2,5,+∞) dziedzina i x<1,5
19 lis 13:35
diks: noi gra

x∊(2,5,1,5)
19 lis 13:37
diks: x∊(−2,5,1,5)
19 lis 13:37
diks: ok następny :
log1/5 (3x−4) ≤ −2
19 lis 13:38
diks: zaraz wracam

19 lis 13:38
Piotr:
pisz średnik miedzy x∊(−2,5 ; 1,5)
19 lis 13:38
diks: ok Piotrze

będę tak pisał

19 lis 13:53
aniabb: i znikł czy liczy

19 lis 13:55
diks: jestem jestem.. ale o 14 do pracy musze iść

19 lis 13:58
diks: ok czyli dziedzina..
19 lis 13:58
aniabb: no to do wieczora

19 lis 13:59
19 lis 13:59
diks: już jest 14?!

19 lis 13:59
diks: o matko..
19 lis 13:59
diks: dziedzina (4/3 ; +∞)
19 lis 14:14
diks: 3x − 4 ≥ (1/5)
−2
3x − 4 ≥ 5
2
3x − 4 ≥ 25
3x ≥ 29
19 lis 14:17
19 lis 14:18
diks: noi wszystko jest ok.. tylko ten pierwszy nawias powinien być otwarty.. ale przecież zmieniłem
znak według wzoru Twojego Aniu

19 lis 14:19
diks: następny to: log2|x−3| > 1
19 lis 14:23
aniabb: jeśli w treści miałeś ≤ to musi być nawias zamknięty
19 lis 14:23
diks: |x−3|>0 jak to opuścić

?
19 lis 14:24
konrad: o, już nierówności

19 lis 14:24
diks: aha rozumiem!

19 lis 14:24
Piotr:
i do pracy nie poszedl

19 lis 14:25
diks: x−3>0
x>3 ?
19 lis 14:25
diks: ide ide zaraz

19 lis 14:25
aniabb: o module >0 mówiliśmy przy równaniach .. to samo co z kwadratami (..)2>0
19 lis 14:26
diks: aha ok

zatem.. (x−3)
2>0
wzór skróconego mnożenia

x
2−6x+9>0
19 lis 14:27
diks: mam liczyć delte?

19 lis 14:27
diks: Δ=b2 −4ac
Δ=(−6)2 − 4*1*9
Δ=36 −36
Δ=0
19 lis 14:28
19 lis 14:29
konrad: 
19 lis 14:29
diks: gdzie się pomyliłem

?
19 lis 14:30
konrad:
|x−3|>0
x−3>0
x>3
end of story jeżeli chodzi o dziedzinę..
19 lis 14:30
konrad: co ja gadam
x∊R\{3}
19 lis 14:31
diks: aa myślałem.. że to co Ania napisała to chodzi o dziedzine

zatem dziedzina to (3 ; +
∞)
19 lis 14:32
konrad: tzn ja właściwie sam nie wiem o co chodzi, ale wydawało mi się że o dziedzinę
i nie, nie (3 ; +∞) bo się pomyliłem
19 lis 14:34
diks: (x−3)2 > 1
x2 − 6x + 9 > 1
x2 − 6x + 8 > 0
19 lis 14:34
diks: dobra ja musze iść do pracy. narazie. będę wieczorem


19 lis 14:35
aniabb: ech.. myślałam ze mu się lepiej skojarzy a tylko namieszałam ..... ten wątek jednak będzie
dłuższy niż poprzedni

19 lis 14:37
19 lis 14:39
aniabb: ZAPOMNIJ CO TERAZ PISAŁAM O KWADRATACH
19 lis 14:39
diks: jest większe ode zera kiedy wykluczymy trójke.. bo dla trójki przyjmuje wartość zero..
dobrze

?
19 lis 15:04
konrad: dobrze, ale co Ty tu robisz?

19 lis 15:08
diks: mam internet w komórce

19 lis 21:58
diks: Dobry wieczór wszystkim...

19 lis 21:59
aniabb: witaj

19 lis 22:00
aniabb: to jaka dziedzina ostatecznie

19 lis 22:02
diks: ide coś zjeść..

i będziemy działać

19 lis 22:16
diks: czyli dziedzina to zbiór liczb rzeczywistych bez trójki?

19 lis 22:39
aniabb: tak

19 lis 22:39
diks: 
19 lis 22:41
aniabb: i dalej..na co czekasz

19 lis 22:44
diks: no niewiem czy to dobrze?

(x−3)
2 > 1
x
2 − 6x + 9 > 1
x
2 − 6x + 8 > 0
19 lis 22:49
aniabb: ZAPOMNIJ CO PISAŁAM O KWADRATACH
19 lis 22:50
diks: to co robić? tak jak poprzednio?
|x−3| > 21 ?
19 lis 22:54
aniabb: tak dokładnie
19 lis 22:54
diks: |x−3| > 2 <−− jak tu opuścić wartość bezwzględną?

19 lis 22:57
diks: |x−3| > 2
x−3 > 2
x>5 ?
19 lis 22:57
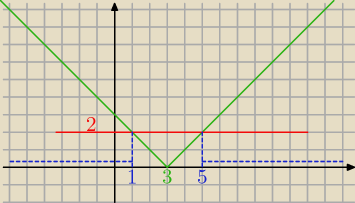
aniabb: a popatrz na rysunek..kiedy zielona jest powyżej y=2

19 lis 22:58
aniabb: |x−3|>2
x−3>2 lub x−3<−2
x>5 lub x<1
19 lis 22:59
19 lis 23:00
diks: przyjmuje wtedy wartości ujemne

19 lis 23:00
diks: czyli x należy
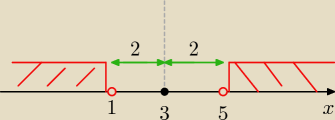
x∊(−∞ ; 1) i (5,+∞)
19 lis 23:04
aniabb:
19 lis 23:05
aniabb: tak
19 lis 23:05
diks: a chodzi Ci, że dla dwójki przyjmuje dwa różne argumenty

?
19 lis 23:06
meta:
19 lis 23:08
diks: kolejny log1/3 |x+2| ≥ −2
19 lis 23:09
diks: możecie mi powiedzieć, co Wy mi rysujecie



?!
19 lis 23:10
diks: dzisiaj.. wyjątko ciężko myśle po pracy..

19 lis 23:10
diks: a wiecie co ide się położyć. będę jutro rano. dobranoc

19 lis 23:11
19 lis 23:13
diks: jest ktoś?

20 lis 09:31
diks: log1/3 |x+2| ≥ −2
20 lis 09:34
diks: dziedzina to będzie zbiór liczb rzeczywistych z wyrzuceniem −2

20 lis 09:35
diks: |x+2| ≥ (1/3)−2
|x+2| ≥ 32
|x+2| ≥ 9
20 lis 09:36
diks: x+2 ≥ 9 lub x+2 ≤ −9
x ≥ 7 lub x ≤ −11
20 lis 09:38
aniabb: jestem

20 lis 09:41
aniabb: przy podstawie ułamkowej ..............................
20 lis 09:41
diks: a tak zmieniamy znaki

20 lis 09:47
diks: x+2| < (1/3)−2
|x+2| < 32
|x+2| < 9
20 lis 09:47
diks: x+2 < 9 lub x+2 > −9
x < 7 lub x > −11
20 lis 09:48
diks: kórde na odwrót chyba..
x+2 > 9 lub x+2 < −9
x > 7 lub x < −11
20 lis 09:49
aniabb: ale zmiana = to =
20 lis 09:53
aniabb: o 9:48 było ok tylko
i między nimi

x∊ <−11;7>
20 lis 09:54
diks: ale przecież jest nierówność, to mam zmienić na równa się?
20 lis 09:55
aniabb: i nie powtarzaj mojego znaki tylko to co pisała Eta : ZWROT nierówności

20 lis 09:56
aniabb: zmiana z ≥ to ≤
20 lis 09:56
diks: odpowiedź jest, że x∊<−11,−2) i (−2,7)
20 lis 09:56
diks: aha

20 lis 09:57
diks: x+2 ≤ 9 lub x+2 ≥ −9
x ≤ 7 lub x ≥ −11
20 lis 09:57
aniabb: 
następne rób ładnie będę za godzinkę .. poczytaj linki
20 lis 09:58
diks: to i tak nie pasuje z odpowiedzią..:(
20 lis 09:58
aniabb: 
następne rób ładnie będę za godzinkę .. poczytaj linki
20 lis 09:59
diks: nam wyszło, że x∊ <−11;7> a w zbiorze jest, że x∊<−11,−2) i (−2,7)
20 lis 10:00
diks: czyżby pierwszy błąd w książce?

20 lis 10:00
diks: aha już jarze

20 lis 10:01
diks: przecież wykluczyliśmy −2

20 lis 10:01
diks: następny log3(x2−4x+3) < 0
20 lis 10:02
diks: x2−4x+3>0
20 lis 10:13
diks: Δ=b2−4ac
Δ=−42 − 4*1*3
Δ=16−12
Δ=4
√Δ=2
20 lis 10:23
20 lis 10:25
20 lis 10:27
diks: zatem dziedzina to zbiór liczb rzeczywistych z wyrzuceniem 1 i 3?
20 lis 10:29
diks: log3(x2−4x+3) < 0
(x2−4x+3) < 30
(x2−4x+3) < 1
x2−4x+2 <0
20 lis 10:30
diks: Δ=b2 −4ac
Δ=16−8
Δ=8
20 lis 10:31
Piotr:
dziedzina źle
20 lis 10:58
aniabb: i znów znikł

20 lis 11:20
Piotr:
witaj
aniabb 
może z

wyszedł

20 lis 11:27
aniabb: albo dosypia na biurku

20 lis 11:28
diks: elo

już jestem.. miałem korepetycje.. nie z majcy

20 lis 13:43
diks: czemu dziedzina źle?>

20 lis 13:44
diks: Piotrze.. aleś Ty dowcipny

20 lis 13:45
konrad: no bo źle, skoro masz nierówność i dwa pierwiastki to rozwiązaniem jest przedział
20 lis 13:46
aniabb: a kiedy parabola jest >0

20 lis 13:46
20 lis 13:46
diks: aaaaaaaa... no tak rzeczywiście!

20 lis 13:46
diks: czesc Konrad

20 lis 13:46
konrad: cze
20 lis 13:47
diks: Dziedzina: x∊(−
∞ ; 1) u (3 ; +
∞)
ramiona paraboli do góry

20 lis 13:52
konrad: yeah
20 lis 13:52
diks: no dobra ale teraz mi coś nie wychodzi.. bo delta wychodzi 8

20 lis 13:54
aniabb: też liczba

a jakie wyniki w książce ?
20 lis 13:55
diks: log3(x2−4x+3) < 0
(x2−4x+3) < 30
(x2−4x+3) < 1
x2−4x+2 <0
Δ=b2 −4ac
Δ=(−4)2 −4*1*2
Δ=16−8
Δ=8
20 lis 13:55
Piotr:
dobrze wychodzi.
√Δ = 2√2
20 lis 13:55
diks: √Δ = √8 = √4*2 = 2√2
20 lis 13:56
20 lis 13:57
konrad: skróć z tą dójką w mianowniku
20 lis 13:58
diks: w odpowiedziach jest:
| | 5−√5 | | 5+√5 | |
x∊( |
| ,2) u (3, |
| ) |
| | 2 | | 2 | |
20 lis 14:00
diks: x1 = 2 + √2
x2 = 2 − √2
20 lis 14:00
diks: a no tak bo źle przepisałem

((((((((((((((((((((((((((
20 lis 14:01
diks: log3(x2−5x+6)<0
20 lis 14:01
diks: (x2−5x+6)>0
20 lis 14:01
aniabb: no to poćwiczyłeś a teraz jeszcze raz

20 lis 14:02
diks: Δ=b2 −4ac
Δ=(−5)2 − 4*1*6
Δ=25−24
Δ=1
20 lis 14:02
Piotr:
robisz identycznie

20 lis 14:02
20 lis 14:03
diks: czyli dziedzina to będą przedziały (−∞ , 2) u (3, +∞)
20 lis 14:04
diks: log3(x2−5x+6)<0
x2−5x+6 < 30
x2−5x+6 < 1
x2−5x+5 <0
20 lis 14:05
Piotr:
widzę literówke

ha !
20 lis 14:05
diks: Δ=b2 − 4ac
Δ=25−20
Δ=5
√Δ=√5
20 lis 14:06
diks: jaką znowu literówke

20 lis 14:06
20 lis 14:07
Piotr:
w x
1 ( jestem w tym specjalista

)
20 lis 14:07
diks: a czemu 2 i 3 też jest w odpowiedzi? jak przecież to jest dziedzina i dodatku nawiasy ma
otwarte przy tych cyfrach?
20 lis 14:08
diks: a no tak Piotrze ma być 6 przez 2

20 lis 14:09
Piotr:
co jest rozwiazaniem tej nierownosci ?
20 lis 14:09
diks: nie wątpie

20 lis 14:09
diks: no x
1 i x
2
20 lis 14:09
diks: to dlaczego oni daja jeszcze w odpowiedziach 2 i 3

20 lis 14:09
Piotr:
rozwiazaniem całej nierownosci log jest czesc wspolna dziedziny i tego co teraz rozwiazales.
20 lis 14:10
aniabb: a co jest rozwiązaniem ostatniej nierówności?
20 lis 14:10
Piotr:
rozwiazaniem nierownosci jest z reguly przedzial

2 msc zerowe! parabola itd

20 lis 14:11
diks: aha

20 lis 14:18
diks: następny:
log1/7(x2+2x−1) ≤ −1
odp: x∊(−∞ , −4> u <2, +∞)
20 lis 14:25
diks: b>0 zatem ..
x2 + 2x − 1 >0
Δ=b2 −4ac
Δ=22 − 4*1*(−1)
Δ=4+4
Δ=8
√Δ = √8 = √4*2 = 2√2
20 lis 14:27
20 lis 14:28
diks: x1 = −1 + √2
x2 = −1 − √2
20 lis 14:29
aniabb: zatem Dziedzina ..
20 lis 14:30
diks: zatem ciąg dalszy nastąpi...
dziedzina wieczorem

spadam do pracy! narazie

20 lis 14:32
Piotr:

20 lis 14:33
diks: Dobry wieczór

poćwiczymy coś?

20 lis 22:28
aniabb: oki
20 lis 22:40
konrad: może tamto najpierw dokończ

20 lis 22:40
diks: hehe

20 lis 22:56
diks: dziedzina: (−∞ ; −1−√2) u (−1+√2 ; +∞) ?
20 lis 22:59
diks: wiecie ile to jest pierwiastek z dwóch?
 √2
√2 = 1,414213562

20 lis 23:00
diks: log1/7(x2+2x−1) ≤ −1
20 lis 23:01
diks: (x2+2x−1) ≤ (1/7)−1
20 lis 23:02
diks: (x2+2x−1) ≤ 71
20 lis 23:02
diks: (x2+2x−1) ≤ 7
20 lis 23:02
diks: x2+2x−8 ≥ 0
20 lis 23:02
diks: Δ=b2 − 4ac
Δ=22 −4*1*(−8)
Δ=4+32
Δ=36
√36 = 6
20 lis 23:03
20 lis 23:04
20 lis 23:04
Eta:
√2=1,4142135623730950488016887242096980785696718753769480731766797...

20 lis 23:07
diks: x∊(−∞ , −4> u <2, +∞)
20 lis 23:08
diks: o matko ETA!

jesteś szalona

!
20 lis 23:08
diks: TWÓJ KALkulator w porównaniu z moim nie ma się co równać

20 lis 23:09
diks: tak a pro po? kto sie mną opiekuje?>

czy wszystko jest ok?

20 lis 23:09
diks: niewiem kiedy zmieniać ten znak gdy mam ułamek do potęgi? odrazu? czy tak jak ja to zrobiłem
teraz

?
20 lis 23:11
Eta:
Jak to ? kto?
minister aniabb 
20 lis 23:12
diks: taką minister to ja mogę mieć

!
20 lis 23:13
diks: ale chyba ich wszystkich wywiało Eta. ZOSTALIŚMY SAMI

20 lis 23:14
diks: no cóż jedziemy dalej..
20 lis 23:14
diks: log8(x2−4x+3) <0
20 lis 23:14
diks: a>0, a≠1, b>0
20 lis 23:15
20 lis 23:15
20 lis 23:18
diks: x
2−4x+3>0
Δ=b
2 −4ac
Δ=(−4)
2 − 4*1*3
Δ=16−12
Δ=4
√Δ=
√4=2
20 lis 23:18
diks: ZMIENIŁEM w momencie gdy przenosiłem siódemke na lewą strone..
20 lis 23:19
diks: dziedzina: x∊(−∞,1) u (3, +∞)
20 lis 23:19
aniabb: To następnym razem 3 linijki wcześniej ..odejmowanie 7 nie zmienia zwrotu
20 lis 23:20
Piotr:
ZMIENIASZ GDY OPUSZCZASZ LOGARYTMY

20 lis 23:21
aniabb: zmieniasz jak przenosisz UŁAMEK z podstawy logarytmu ..było przenoszone 1/7
20 lis 23:21
diks: aha rozumiem.. czyli odrazu będę zmieniać.. gdy tylko będzie ułamek i będe go przenosić

20 lis 23:23
diks: x2 − 4x + 3 < 80
x2 − 4x + 3 < 1
x2 − 4x + 2 <0
Δ = 8
√Δ = 2√2
20 lis 23:24
diks: x1 = 2+√2
x2 = 2−√2
20 lis 23:25
diks: x∊(2−√2,1) u (3,2+√2)
20 lis 23:25
diks: następny:
log1/2(5+4x−x2) > −3
20 lis 23:26
diks: a>0 , a≠1 , b>0
20 lis 23:27
aniabb: ok

20 lis 23:29
diks: −x
2 + 4x + 5 > 0
Δ=b
2 − 4ac
Δ=4
2 −4*(−1) * 5
Δ=16+20
Δ=36
√Δ=6
| | −4+6 | | 2 | |
x1 = |
| = |
| = −1 |
| | 2*(−1) | | −2 | |
| | −4−6 | | −10 | |
x2 = |
| = |
| = 5 |
| | 2*(−1) | | −2 | |
dziedzina: x∊(−1,5)
20 lis 23:31
diks: log1/2(5+4x−x2) > −3
−x2 + 4x + 5 < −31/2
20 lis 23:33
diks: −3
1/2 = −
√3 

20 lis 23:33
20 lis 23:40
diks: 1/2

20 lis 23:41
diks: a no tak racja

20 lis 23:41
diks: −x2 + 4x + 5 > (1/2)−3
20 lis 23:42
diks: −x2 + 4x + 5 < 23
20 lis 23:42
aniabb: 
20 lis 23:42
diks: −x2 + 4x + 5 < 8
20 lis 23:42
diks: −x2 + 4x − 3 < 0
20 lis 23:43
diks: ok ja mykam jutro dokończe. dobranoc

w tym tygodniu mam jakiś spadek formy

20 lis 23:52
diks: Δ=b2 − 4ac
Δ=42 − 4*(−1)*(−3)
Δ=16−12
Δ=4
√Δ = 2
21 lis 08:21
aniabb: 
21 lis 08:23
21 lis 08:27
diks: rozwiązanie nierówności: (−∞,1) u (3,+∞)
dziedzina: (−1,5)
zatem x∊(−1,1) u (3,5)
21 lis 08:29
diks: następny:
log1/5(2x+1) < log1/5(16−x2) + 1
21 lis 08:30
diks: a>0 , a≠1 , b>0
21 lis 08:31
21 lis 08:31
diks: 16−x2 > 0
−x2 > −16 /*(−1)
x2 ≤< 16
x=4 lub x= −4
21 lis 08:33
diks: zatem dziedzina to x∊(−1/2, +∞)
21 lis 08:34
aniabb: a z tej nierówności kwadratowej ?
21 lis 08:36
diks: no właśnie niewiem co z tymi czwórkami


?
21 lis 08:39
aniabb: oś ..czwórki ..parabolka..i przedział rozwiązania
21 lis 09:02
diks: (−∞,−4> u <4, +∞)
21 lis 09:18
diks: x
2 ≤ 16 chyba

?
21 lis 09:22
diks: no bo x2 nie może być mniejsze od 16 jeżeli bierzemy pod uwage 4 i −4, przecież obie czwórki
podniesione do kwadratu dadzą 16, więc zmieniłem znak z mniejszego na mniejsze, bądź równe..
21 lis 09:23
gizmo: czyli prawa połówka pasuje mi do dziedziny, a lewa nie ?

21 lis 09:29
diks: tak

21 lis 09:29
21 lis 09:31
diks: przecież już Ci Ania pomogła

21 lis 09:32
diks: log1/5(2x+1) < log1/5(16−x2) + 1
21 lis 09:33
diks: log1/5(2x+1) − (log1/5(16−x2) + 1) < 0
21 lis 09:34
diks: log1/5(2x+1) − log1/5(16−x2) < −1
21 lis 09:34
Aga1.: x2−16<0
x∊(−4,4)
21 lis 09:35
diks: log1/5(2x+1) − (16−x2) < (1/5)−1
21 lis 09:35
diks: czemu tak Aga?

21 lis 09:36
diks: log1/5(2x+1) − (16−x2) < 5
21 lis 09:36
diks: log1/5(2x+1) − (16−x2) > 5
21 lis 09:36
diks: JAK PRZECIEż miałem 16−x2 > 0
21 lis 09:37
diks: 
a jakbym podziedzlił przez siebie te logarytmy? bo w sumie to mają tą samą podstawe

21 lis 09:40
Aga1.:
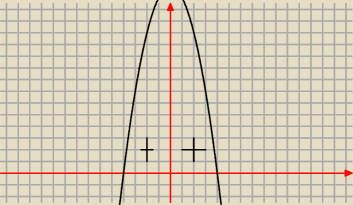
16−x
2>0 dla x∊(−4,4)
21 lis 09:40
diks: a no tak RZECZYWIŚCIE


MASZ racje

21 lis 09:42
Aga1.: O 9:35 źle zapisałeś
21 lis 09:43
diks: zatem dziedzina ogólna to będzie.. (−4, +
∞)?

21 lis 09:44
diks: zatem o 9:34 było dobrze?

log
1/5(2x+1) − log
1/5(16−x
2) < −1
21 lis 09:46
diks: i teraz: (2x+1) : (16−x
2)

21 lis 09:48
Aga1.:
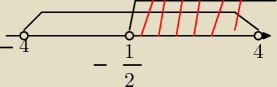
| | −1 | |
x> |
| i x∊(−4,4) to część wspólna |
| | 2 | |
x∊(−1/2,4) i to jest dziedzina
21 lis 09:50
aniabb: ech...
log1/5(2x+1) < log1/5(16−x2) + 1
log1/5(2x+1) < log1/5(16−x2) + log1/5 1/5
log1/5(2x+1) < log1/5(1/5(16−x2))
2x+1 > 1/5 * (16−x2)
21 lis 09:51
Aga1.: Teraz lepiej , chociaż ja robiłabym inaczej, ale nie chcę Ci mętliku robić w głowie.
21 lis 09:52
diks: aha

21 lis 09:53
aniabb: tia..przeniosłeś jedynkę w tę i z powrotem i nagle zmieniła znak ...

rzeczywiście lepiej ...
a równanka tak ładnie Ci szły

21 lis 09:54
21 lis 09:58
diks: 10x + 5> 16 − x2
21 lis 09:58
diks: x2 + 10x − 11 > 0
21 lis 09:59
aniabb: 
21 lis 10:00
diks: Δ=b2 −4ac
Δ=102 − 4*1*(−11)
Δ=100 + 44
Δ=144
√Δ = 12
21 lis 10:02
diks:
| | −10−12 | | −22 | |
x2 = |
| = |
| = −11 |
| | 2 | | 2 | |
21 lis 10:03
Aga1.: Ok. licz dalej.
21 lis 10:04
diks: (−∞, −11) u (1,+∞)
21 lis 10:05
diks: dziedzina: (−1/2,4)
21 lis 10:05
diks: zatem x∊(1,4)?
21 lis 10:06
Aga1.: ok.
21 lis 10:14
diks: NASTĘPNy:
log1/2(5x+10) < log1/2(x2+6x+8)
21 lis 10:15
diks: a>0 a≠1 b>0
21 lis 10:15
diks: 5x+10>0
5x> −10
x> −2
21 lis 10:15
aniabb: 
21 lis 10:16
diks: x
2 + 6x + 8 >0
Δ=b
2 − 4ac
Δ=6
2 − 4*1*8
Δ=36−32
Δ=4
√Δ = 2
21 lis 10:17
diks: zatem mamy:
1. x>−2, zatem (−2, +∞)
2. x1= −2 i x2= −4, zatem (−∞,−4) u (−2, +∞)
21 lis 10:20
diks: dziedzina to (−2,+
∞) ?

21 lis 10:20
Aga1.: ok.
21 lis 10:22
aniabb: tak

21 lis 10:22
diks: 
21 lis 10:28
diks: tylko teraz co dalej

log
1/2(5x+10) < log
1/2(x
2+6x+8)
5x+10 > x
2+6x+8
−x
2 −x +2 > 0
21 lis 10:30
aniabb: brawo

21 lis 10:31
diks: Δ=b
2 − 4ac
Δ=(−1)
2 − 4*(−1) * 2
Δ=1+8
Δ=9
√Δ = 3
| | 1+3 | | 4 | |
x1 = |
| = |
| = −2 |
| | 2*(−1) | | −2 | |
| | 1−3 | | −2 | |
x2 = |
| = |
| = 1 |
| | 2*(−1) | | −2 | |
21 lis 10:56
diks: zatem rozwiązanie to: (−2,1)
dziedzina: (−2,+∞)
zatem x∊(−2,1)
21 lis 10:59
diks: teraz mamy coś takiego:
21 lis 11:00
diks: a>0, a≠1, b>0
mianownik ≠ 0
21 lis 11:01
diks: x+1> 0
x> −1
2x−3>0
2x>3
21 lis 11:02
aniabb: 
21 lis 11:03
diks: dziedzina to przedział: (1,5 ; +∞)
21 lis 11:03
21 lis 11:04
diks: ok chyba wszystkie założenia spełnione..
21 lis 11:06
21 lis 11:07
diks: | | 1 | |
no niestety odpowiedź to (1 |
| ,4> więc źle to robie  |
| | 2 | |
21 lis 11:09
aniabb: dziedzina źle.. cały ułamek ma być dodatni to nie tylko góra i dół dodatnie ale również góra i
dół ujemne jednocześnie
21 lis 11:09
aniabb: jak nie ma nic przy log tzn że jest 10 ... ≥100
21 lis 11:10
21 lis 11:13
21 lis 11:13
diks: −x ≥ −4 /* (−1)
x ≤ 4
21 lis 11:14
diks: nie rozumiem o co Ci chodzi z dziedziną

21 lis 11:15
aniabb: 1 na drugą stronę i do wspólnego mianownika
to NIERÓWNOŚCI mozna mnożyć tylko przez na pewno DODATNIĄ
czyli zazwyczaj kwadrat mianownika
21 lis 11:15
aniabb: Dziedzina b>0
| | x+1 | |
b= |
| >0 //*(2x−3)2 |
| | 2x−3 | |
(x+1)(2x−3) >0
i dalej ...
21 lis 11:17
diks: aha ja sobie podzieliłem to na dwa logarytmy dziesiętne i na dwa b
21 lis 11:19
aniabb: nie można
21 lis 11:19
diks: 2x2 −x −3 >0
21 lis 11:20
diks: Δ=b
2 − 4ac
Δ=(−1)
2 − 4*2*(−3)
Δ=1+24
Δ=25
√Δ = 5
x∊(−
∞, −1) u (1,5 ; +
∞)
21 lis 11:24
diks:
| x+1 | | 1*(2x−3) | |
| − |
| ≥ 0 |
| 2x−3 | | 2x−3 | |
(4−x)(2x−3) ≥ 0
8x −12 −2x
2 + 3x ≥ 0
−2x
2 + 11x − 12 ≥ 0
21 lis 11:28
diks: Δ=b2 −4ac
Δ=112 − 4*(−2)*(−12)
Δ=121−96
Δ=25
√Δ = 5
21 lis 11:30
diks: | | −11+5 | | −6 | | 3 | |
x1 = |
| = |
| = |
| |
| | 2*(−2) | | −4 | | 2 | |
| | −11−5 | | −16 | |
x1 = |
| = |
| = 4 |
| | 2*(−2) | | −4 | |
21 lis 11:31
aniabb: ładnie tylko po co liczysz Δ jak już masz mnożenie

(4−x) = 0 lub (2x−3) = 0
21 lis 11:31
21 lis 11:31
diks: a no tak rzeczywiście

masz racje

21 lis 11:33
diks: | | 3 | |
zatem rozwiązaniem jest x∊( |
| ,4> |
| | 2 | |
21 lis 11:35
aniabb: chyba tak

21 lis 11:37
diks: | | 2x2 −4x − 6 | |
log1/2 |
| ≤ −1 |
| | 4x−11 | |
21 lis 11:49
aniabb: 
ładny

21 lis 11:50
diks: bardzoo ładny

!
21 lis 11:50
diks: a>0, a≠1, b>0
mianownik ≠ 0
21 lis 11:51
diks: | 2x2 −4x − 6 | |
| > 0 /* (4x−11)2 |
| 4x−11 | |
(2x
2 −4x − 6)*(4x−11) > 0
21 lis 11:52
aniabb: i z pierwszego nawiasu delta
21 lis 11:53
diks: Δ= b
2 − 4ac
Δ=(−4)
2 − 4*2*(−6)
Δ=16+48
Δ=64
√Δ = 8
21 lis 11:54
diks: | | 11 | |
x∊(−∞,−1) u (3,+∞) i x= |
| |
| | 4 | |
21 lis 11:55
konrad: źle.....
21 lis 12:00
aniabb:
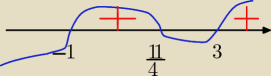
jak policzyłeś deltę to masz iloczyn
2(x−3)(x+1)(4x−11) >0
taki wielomian wężykiem robimy ( rys)
21 lis 12:20
konrad: znowu go wcięło

21 lis 13:29
diks: JESTEm miałem korki z majcy

21 lis 13:51
diks: aha

ok czyli będę wiedział.. że jak takie coś to wężyk..
21 lis 13:52
diks: | | 11 | |
czyli dziedzina to: przedziały (−1, |
| ) u (3, + ∞)  |
| | 4 | |
21 lis 23:29
konrad: tak
21 lis 23:33
zombi: Diks? Jak Krzysztof Diks z potyczek algorytmicznych?
21 lis 23:53
diks: | | 2x2−4x−6 | |
log1/2 |
| ≤ −1 |
| | 4x−11 | |
21 lis 23:54
diks: hehe...

chciałbym

!
21 lis 23:56
diks: | 2x2 −4x − 6 | | 2(4x−11) | |
| − |
| ≥ 0 |
| 4x−11 | | 4x−11 | |
| 2x2 −4x − 6 | | 8x−22) | |
| − |
| ≥ 0 |
| 4x−11 | | 4x−11 | |
| (2x2 −4x − 6)−(8x−22) | |
| ≥ 0 |
| 4x−11 | |
| (2x2 −4x − 6)−(8x−22) | |
| ≥ 0 |
| 4x−11 | |
| (2x2 −4x − 6 − 8x + 22) | |
| ≥ 0 |
| 4x−11 | |
| (2x2 −12x + 16) | |
| ≥ 0 / * (4x−11)2 |
| 4x−11 | |
(2x
2−12x+16)(4x−11) ≥ 0
22 lis 00:10
diks: 
22 lis 00:14
ZKS:

.
22 lis 00:18
diks: Δ=b
2 − 4ac
Δ=(−12)
2 −4*2*16
Δ=144−128
Δ=16
√Δ=4
22 lis 09:17
22 lis 09:18
22 lis 09:21
diks: a>0, a≠1, b>0
mianownik ≠ 0
x−1≠0
x≠1
22 lis 09:24
diks:
3(x−1) > 0
3x − 3 > 0
3x > 3 /:3
x > 1
5−x>0
−x>−5 /*(−1)
x<5
22 lis 09:25
diks: dziedzina: x∊(1,5)
22 lis 09:25
diks:
| 3 | | (5−x)(x−1) | |
| − |
| > 0 |
| x−1 | | x−1 | |
| 3 | | (5x−5−x2+x) | |
| − |
| > 0 |
| x−1 | | x−1 | |
| x2 −6x +8) | |
| > 0 / *(x−1)2 |
| x−1 | |
(x
2 −6x +8)(x−1)+ > 0
Δ=b
2 −4ac
Δ=(−6)
2 −4*1*8
Δ=36−32
Δ=4
√Δ = 2
x
3 = 1
x∊(1,2) u (4,+
∞)
dziedzina: x∊(1,5)
zatem x∊(1,2) u (4,5)
22 lis 09:36
Aga1.:

Popraw dziedzinę, obliczenia w porządku.
22 lis 09:37
diks: | | 2 | |
następy: log1/4(2−x) > log1/4 |
| |
| | x+1 | |
22 lis 09:37
diks: przecież wyszło dla dziedziny, że x jest większe od 1 i mniejsze od 5.. to część wspólna to
będzie przedział (1,5)?

22 lis 09:39
Aga1.: Ja widzę,że napisałeś x≠1, co oznacza, że x∊(−∞,1)U(1,∞).
Nigdzie nie ma x>1
22 lis 09:41
diks: jest
22 lis 09:25

b>0
22 lis 09:42
diks: tak x≠1 bo mianownik musi być różny od zera

22 lis 09:42
Aga1.: Przepraszam, jest jeszcze trzeci warunek i jest ok.
22 lis 09:44
diks: to już niewiem czy mam dobrze, czy mam źle

22 lis 09:52
Aga1.: Napisałam,że jest wszystko dobrze, bo nie zauważyłam warunku x>1.
Licz następny przykład, to Ci chwilę poasystuję.
22 lis 09:56
diks: zatem założenia: a>0 a≠1 b>0
22 lis 09:57
diks: mianownik ≠ 0
x+1 ≠ 0
x ≠ −1
22 lis 09:57
diks: 2−x > 0
−x > −2 (*(−1)
x < 2
2(x+1) > 0
2x + 2 > 0
2x > −2 /:2
x > −1
22 lis 09:59
diks: x< 2 i x> −1
zatem dziedzina to przedział: x∊(−1,2)
22 lis 10:00
Aga1.: c>0 i co dalej?
22 lis 10:00
diks: | | 2 | |
log1/4(2−x) > log1/4 |
| |
| | x+1 | |
22 lis 10:02
diks: jakie znowu c>0?

22 lis 10:02
Aga1.: | 2 | |
| >0 /*(x+1)2 , dalsze obliczenia poprawne |
| x+1 | |
22 lis 10:03
Aga1.: Mój komputer bardzo wolno chodzi , stąd to opóźnienie.
22 lis 10:04
diks: | (2−x)(x+1) | | 2 | |
| − |
| > 0 |
| x+1 | | x+1 | |
| (2x+2 −x2 −x) | | 2 | |
| − |
| > 0 |
| x+1 | | x+1 | |
| (2x+2 −x2 −x −2) | |
| > 0 /*(x+1)2 |
| x+1 | |
(−x
2 +x)(x+1) > 0
22 lis 10:10
aniabb: A jaka była PODSTAWA


22 lis 10:14
diks: Cześć Aniu.. no właśnie nie wiedziałem czy tu też zmieniać znak nierówności bo w sumie tu
opuszczam podstawe a przedtem przenosiłem ułamek z podstawy

22 lis 10:16
Aga1.: A jaka jest podstawa logarytmu?
22 lis 10:16
diks: (−x2 +x)(x+1) < 0
22 lis 10:17
aniabb: jak znika log z podstawą ułamkową zmieniasz zwrot
22 lis 10:17
aniabb: tak

22 lis 10:18
diks: Δ=b
2 − 4ac
Δ=1
2−4*(−1)*0
Δ=1
√Δ = 1
x
3 = −1
22 lis 10:18
diks: zatem x∊(−1,0) u (1,2)
22 lis 10:19
aniabb: oki
22 lis 10:19
aniabb: odwrotnie
22 lis 10:19
aniabb: jak przy najwyższej potędze minus to wężyk zaczynasz od dołu licząc od końca
22 lis 10:20
diks: następny:
log1/3[log4(x2−5)] > 0
22 lis 10:20
aniabb: aa ok..tam było ograniczenie z dziedziny

22 lis 10:22
diks: źle tamto? w odpowiedziach na końcu jest tak samo jak mi wyszło o 10:19

22 lis 10:22
aniabb: zawsze pisałeś najpierw rozw.. a potem dopiero z dziedziną .. zabrakło mi nieskończoności..a
jak zaczęłam rysować okazało się ze masz dobrze

22 lis 10:23
diks: hehe.. w takim razie wrócimy do rozwiązań

odpowiedź do tej nierówności to: x∊(−3,−
√6) u (
√6,3)
22 lis 10:29
diks: a>0 a≠1 b>0
22 lis 10:29
diks: o lol

my tu mamy dwa logarytmy związane ze sobą 0.o
22 lis 10:30
diks: x2 − 5 > 0
x2 > 5
x = √5
22 lis 10:30
diks: [log4(x2−5)] < (1/3)0
[log4(x2−5)] < 1
22 lis 10:32
diks: log4(x2−5)< 1
22 lis 10:33
diks: log4(x2−5) − 1 < 0
22 lis 10:34
aniabb: drugi warunek dziedziny log4(x2−5) >0
22 lis 10:34
aniabb: w rozwiązaniu drugi logarytm jak pierwszy przenosisz 4
log4(x2−5)< 1
x2−5< 41
22 lis 10:35
diks: log4(x2−5) >0
(x2−5) > 40
(x2−5) > 1
x2 > 6
x> √6
22 lis 10:41
diks: log4(x2−5)< 1
x2−5< 41
x2 − 5 < 4
x2 < 9
x < 3 lub x < −3
22 lis 10:42
diks: dziedzina: x∊(√6 , +∞)
22 lis 10:45
aniabb: to teraz ten post o 10:41 rozwiąż tak dobrze jak ten następny

22 lis 10:45
aniabb: dziedzina źle
22 lis 10:45
aniabb: aa ten następny też źle

22 lis 10:46
aniabb: ech...
x
2 − a
2 = (x−a)(x+a) i wężykiem skoro zapominasz że to parabola

22 lis 10:47
diks: x > √6 lub x > −√6
22 lis 10:47
diks: a gdzie ja mam niby takie coś? x2 − a2 = (x−a)(x+a)
22 lis 10:48
aniabb:
x2<9 ⇔ x2−9 < 0
x2>6 ⇔ x2−6 > 0
22 lis 10:49
aniabb: zamieniasz zawsze na nawiasy i rysujesz WĘŻYK
22 lis 10:50
diks:
x2−9 = (x−3)(x+3)
x2−6 = (x−√6)(x+√6)
22 lis 10:59
diks: wyszły mi 4 punkty na osi: −3, −√6 , √6 , 3
22 lis 11:02
aniabb: to są oddzielne rzeczy najpierw dziedzinę ..2 punkty ..potem rozwiazanie zadania 2 punkty i
dopiero część wspólna
22 lis 11:04
diks: mi sie to wszystko już pomieszało

22 lis 11:11
aniabb: to od początku .. dziedzina :
22 lis 11:13
diks: dla dziedziny wyszło.. x2 > 5 i x2> 6
22 lis 11:19
aniabb: no to pierwsza nierówność ... wężyk ..co wychodzi
22 lis 11:22
diks: dziedzina: (−∞,−√6) u (−√5,√5) u (√6,+∞)?
22 lis 11:33
diks: dobrze?

22 lis 11:37
aniabb: pierwsza nierówność
22 lis 11:37
diks: x2 > 5
22 lis 11:38
diks: (−∞,−√5) u (√5, +∞)
22 lis 11:39
aniabb:

x
2 −5 >0 ⇔ x∊(−
∞;−
√5) u (
√5;
∞)
22 lis 11:40
aniabb: a teraz druga nierówność
22 lis 11:40
diks: x2> 6
(−∞, −√6) u (√6, +∞)
22 lis 11:45
aniabb: brawo

a teraz ostatecznie dziedzina

22 lis 11:46
diks: dziedzina: (−∞,−√5) u (√5, +∞) i (−∞, −√6) u (√6, +∞)
22 lis 11:47
diks: zatem dziedzina to będzie...
22 lis 11:47
diks: (−
∞, −√6) u (√6, +
∞)

22 lis 11:47
aniabb: 
22 lis 11:48
aniabb: to teraz rozwiązujemy przykład
22 lis 11:49
diks: 
22 lis 11:49
diks: x2 < 9
x∊(−3,3)
22 lis 11:51
aniabb: super

22 lis 11:55
aniabb: to teraz formułujemy odpowiedź ( jak to się ładnie w kluczach odpowiedzi nazywa )
22 lis 11:56
diks: zatem x∊(−3,−√6) u (√6 , 3)
22 lis 12:00
diks: 
przetrwaliśmy

22 lis 12:01
diks: | | 1+2x | |
log1/2(log2 |
| ) > 0 |
| | 1+x | |
22 lis 12:02
diks: a>0 a≠1 b>0
22 lis 12:03
diks: mianownik ≠ 0
1+x ≠ 0
x ≠ −1
22 lis 12:04
aniabb: uff

22 lis 12:08
diks:
(1+2x)(1+x) > 0
1 + x + 2x + 2x
2 > 0
Δ= b
2 −4ac
Δ=3
2 − 4*2*1
Δ=9−8
Δ=1
√Δ = 1
| | −3+1 | | −2 | | 1 | |
x1 = |
| = |
| = − |
| |
| | 4 | | 4 | | 2 | |
22 lis 12:13
22 lis 12:14
aniabb: no i wężyk
22 lis 12:14
diks: jak zwykle nie myśle

22 lis 12:17
diks: | | 1 | |
a więc x∊(−∞ , −1) u (− |
| , +∞) |
| | 2 | |
22 lis 12:19
aniabb: ok .............. teraz druga liczba logarytmowana >0
22 lis 12:22
diks:
x(1+x) > 0
x
2 + x > 0
Δ=b
2 − 4ac
Δ=1
2 − 4*1*0
Δ=1
√Δ=1
x∊(−
∞,−1) u (0,+
∞)
22 lis 12:30
diks: zatem dziedzina to x∊(−∞,−1) u (0,+∞)
22 lis 12:32
aniabb: i znów delta jak miałeś mnożenie

OK
22 lis 12:34
diks: | | 1+2x | |
log1/2(log2 |
| ) > 0 |
| | 1+x | |
−1(1+x)<0
−1−x<0
−x<1 /*(−1)
x > −1
22 lis 12:42
diks: zatem x∊(0,+∞)
22 lis 12:42
aniabb: 
22 lis 12:44
diks: 
22 lis 12:46
diks: następny:
| | x2−2x | |
log1/2(log8 |
| ) < 0 |
| | x−3 | |
22 lis 12:47
diks: a>0 a≠1 b>0
22 lis 12:47
diks: mianownik ≠0
x−3≠0
x≠3
22 lis 12:48
diks: (x
2−2x)(x−3) > 0
Δ=b
2 −4ac
Δ=(−2)
2 −4*1*0
Δ=4
√Δ = 2
x
3 = 3
x∊(−
∞,0) u (2,+
∞)
22 lis 12:54
diks: | x2−2x | | 1(x−3) | |
| − |
| > 0 |
| x−3 | | x−3 | |
| x2 − 3x +3) | |
| > 0 / *(x−3)2 |
| x−3 | |
(x
2 − 3x +3)(x+3) > 0
Δ=b
2−4ac
Δ=(−3)
2−4*1*3
Δ=9−12
Δ= −3
22 lis 13:01
aniabb: o 12:54 jak masz trzy iksy to jak wygląda węzyk

22 lis 13:02
aniabb: o 13:01 jak delta ujemna to ten pierwszy nawias zawsze dodatni czyli sprawdzamy tylko drugi
22 lis 13:03
diks: a no tak masz racje

22 lis 13:27
diks: jeżeli chodzi o dziedzine..
to x∊(0,2) u (3, +∞)
22 lis 22:57
diks: x+3>0
x>−3
22 lis 22:58
aniabb: tak
22 lis 22:58
diks: moment..
to było do pierwszego b>0
x∊(0,2) u (3, +∞)
natomiast drugie b>0
x>−3
22 lis 22:59
diks: przepraszam ma być x−3>0 czyli x>3
22 lis 23:00
diks: zatem dziedzina to będzie: część wspólna, czyli
x∊(3, +∞)
22 lis 23:01
diks: i teraz w sumie możemy już liczyć

22 lis 23:03
aniabb: OK

22 lis 23:03
diks: | | x2−2x | |
log1/2(log8 |
| < 0 |
| | x−3 | |
| | x2−2x | |
log8( |
| ) > (1/2)0 |
| | x−3 | |
| x2−2x | | 8(x−3) | |
| − |
| > 0 |
| x−3 | | x−3 | |
| x2−2x | | (8x−24) | |
| − |
| > 0 |
| x−3 | | x−3 | |
| x2 −10x −24 | |
| > 0 /*(x−3)2 |
| x−3 | |
(x
2 −10x −24)(x−3) >0
Δ=b
2 −4ac
Δ=(−10)
2 −4*1*(24)
Δ=100−96
Δ=4
√Δ=2
x
3= 3
dziedzina: x∊(3, +
∞)
odpowiedź: x∊(3,4) u (6,+
∞)
22 lis 23:15
diks: chyba dobrze wyszło.. bo zgadza się z rozwiązaniem na końcu

22 lis 23:16
aniabb: prawie dobrze .. −(−24) = +24
22 lis 23:16
aniabb: dobrze wyszło bo w delcie zgubiłeś ten błędny minus

22 lis 23:17
22 lis 23:17
diks: a no tak.. to błąd przepisywania

22 lis 23:18
Piotr:
siemanko

nie miales miec dzisiaj tego kolokwium ?

22 lis 23:18
diks: a>0 a≠1 b>0
22 lis 23:19
diks: niee.. jeszcze mi trochę zostało czasu

22 lis 23:19
diks: wsumie został mi tylko piątek jeszcze

22 lis 23:20
diks: a nam zostało 19 nierówności

22 lis 23:21
diks: i to tych najgorszych

22 lis 23:21
aniabb: i co ja będę robić w przyszłym tygodniu

22 lis 23:21
diks: ale tydzień nam zajeły równania

a ten tydzień to już prawie same nierówności

22 lis 23:22
diks: no cóż w przyszłym tygodniu będziesz mi pomgać robic granice jakieś

bo właśnie to zaczynam w
tą sobote...
22 lis 23:22
diks: a narazie to mi coś podpowiedz do tego przykładu co teraz mamy

22 lis 23:24
diks: bo nie mam tutaj nawiasu pomiędzy tymi logarytmami.. jak to było w poprzednim przykładzie..
22 lis 23:25
aniabb: to go sobie narysuj

22 lis 23:27
diks: to się da narysować

?!
22 lis 23:34
aniabb: nawias ..zawsze )
22 lis 23:35
aniabb: tu go nie ma bo jednej rzeczy nie trzeba brać w nawias, ale można
22 lis 23:38
diks: ha.. dobre

!
22 lis 23:38
diks: rozumiem.. czyli po prostu postępuje tak jak z poprzednimi ?

22 lis 23:39
diks: (x
2+x)(x+4) > 0
Δ=b
2 −4ac
Δ=1
2−4*1*0
Δ=1
√Δ = 1
x
3 = −4
x∊(−4,−1) u (0,+
∞)
22 lis 23:44
aniabb: ok
22 lis 23:48
diks: Aniu o której będziesz jutro?

22 lis 23:54
aniabb: od 7 do 14 ..a potem pewnie wieczorem koło 19stej
22 lis 23:56
diks: (x
2−4)(x+4) > 0
Δ=b
2 −4ac
Δ=0
2 − 4*1*(−4)
Δ=16
√Δ=4
x
3= −4
x∊(−4,−2) u (2, +
∞)
23 lis 00:01
konrad: diks, co Ty ciągle z tą deltą

23 lis 00:01
diks: dziedzina: x∊(−4,−2) u (2, +∞)
23 lis 00:01
diks: cześć Konrad

ćwicze i ćwicze

23 lis 00:02
konrad: hehe, to ćwicz, bo liczenie bez delty Ci zaoszczędzi czasu, szczególnie gdy jej liczenie jest
zbędne

23 lis 00:05
diks: | | x2+x | |
logo,3[log6( |
| )] < 0 |
| | x+4 | |
(x
2−5x−24)(x+4) > 0
Δ=b
2 −4ac
Δ=(−5)
2 −4*1*(−24)
Δ=25+96
Δ=121
√Δ = 11
x
3 = −4
dziedzina: x∊(−4,−2) u (2, +
∞)
odpowiedź: x∊(−4,−3) u (8,+
∞)
23 lis 00:08
diks: to jak sobie z tym poradzić niby bez delty

?!
23 lis 00:08
aniabb: OK
23 lis 00:11
aniabb: czasem wystarczyło wyciągnąć x przed nawias ( wszędzie tam gdzie któryś x wychodził z delty
zero )
albo wzor skróconego mnożenia

(jak było x
2−2
2)
23 lis 00:12
diks: następny:
log
21/2x −2log
1/2x −3 < 0
23 lis 00:13
diks: no to teraz się zaczynają przyjemnie przykłady

23 lis 00:13
diks: ma ktoś jakiś pomysł na tą nierówność?

23 lis 00:14
diks: dobra.. może cos wykombinujemy jutro.. dobranoc

!
23 lis 00:18
aniabb: dziedzina ... log1/2x = t
23 lis 00:19
Piotr:
standardowo podstawienie

23 lis 00:19
pigor: ... no właśnie taka jest oto polska szkoła , delta

i nic więcej,
a można − nawet nie podając dziedziny (dlaczego ?) − np. tak :
| | x2+x | | x2+x | |
log 6 |
| >0 ⇔ |
| >1 /*(x+4)2 i x≠−4 ⇒ (x2+x)(x+4)−(x+4)2 >0 ⇔ |
| | x+4 | | x+4 | |
⇔ (x+4)(x
2+x−x−4) >0 ⇔ (x+4)(x−2)(x+2) >0 ⇔
−4< x<−2 lub x>2 ⇔
⇔
x∊(−4;−2) U (2;+∞) . ...

23 lis 00:27
diks: x>0
zatem dziedzina to przedział: (0,+∞)
23 lis 09:16
aniabb: witam

23 lis 09:16
diks: log1/2 = t
t2 − t − 3 <0
23 lis 09:17
diks: dzień dobry Aniu

23 lis 09:17
aniabb: dwójkę zjadłeś ..czyżby w ramach śniadania...

jak smakowała

23 lis 09:19
diks: Δ=b2 −4ac
Δ=(−1)2 −4*1*(−3)
Δ=1+12
Δ=13
23 lis 09:19
diks: hehe.. masz racje

23 lis 09:19
diks: t2 − 2t − 3 <0
23 lis 09:20
aniabb: i poszedł na śniadanie

23 lis 10:04
diks: hehe jestem już

23 lis 11:10
aniabb: no to dalej..
23 lis 11:10
diks: Δ=b2 −4ac
Δ=(−2)2 −4*1*(−3)
Δ=4+12
Δ=16
√Δ = 4
23 lis 11:10
23 lis 11:14
diks: x∊(−1,3)
23 lis 11:15
diks: dziedzina: (0,+∞)
23 lis 11:15
diks: log
1/2x = 3
U({1}{2})
3 = x
23 lis 11:17
diks: log1/2 = −1
(1/2)−1 = x
x = 2
23 lis 11:18
23 lis 11:18
aniabb: no i ciekawe co ci wyjdzie

23 lis 11:18
diks: kolejny:
−2log24x + 3log4x − 1 > 0
23 lis 11:20
aniabb: farciarz .. nieświadomie pozmieniałeś zwroty nierówności

23 lis 11:20
diks: x>0 dziedzina: (0,+∞)
23 lis 11:21
diks: że co?

! JAK pozmieniałem? nie nie zmieniałem

23 lis 11:22
aniabb: ale na klasówce :
−1 < t < 3
log1/2x >−1
x < 2
log1/2x <3
x >1/8
23 lis 11:23
diks: co z tym zrobiłaś.. że zmieniły Ci się znaki nierówności?
log1/2x >−1
x < 2
log1/2x <3
x >1/8
23 lis 11:24
aniabb: PODSTAWA ułamek ...
23 lis 11:26
diks: a no tak

23 lis 11:27
diks: ok to w takim razie bierzemy się za kolejny

23 lis 11:28
diks: log4x = t
23 lis 11:28
diks: −2t2 +3t − 1 > 0
23 lis 11:28
Piotr:
oj diks nieładnie

tye nauki

23 lis 11:29
diks: Δ=b
2 −4ac
Δ=3
2 −4*(−2)*(−1)
Δ=9−8
Δ=1
√Δ=1
| | −3+1 | | −2 | | 1 | |
t1 = |
| = |
| = − |
| |
| | −4 | | −4 | | 4 | |
23 lis 11:30
Piotr:
chodzilo mi o ulamek jak cos

23 lis 11:30
23 lis 11:31
diks: możecie mi powiedzieć ile to jest (1/4)
1/4?

23 lis 11:33
diks: za ułamek przepraszam

23 lis 11:34
aniabb: √1/2 = √2/2
23 lis 11:34
aniabb: gdzieś masz błąd...no taaak ...2/4 = 1/4


23 lis 11:35
diks: czyli..
x > √2/2
x < 4
23 lis 11:36
Piotr:
he he

23 lis 11:36
diks: o matko...1/2

23 lis 11:36
23 lis 11:48
diks: (1/4)1/2 =x
23 lis 11:48
diks: i co teraz? z tym zrobić

?
23 lis 11:49
diks: nie umiem podnosić ułamek do potęgi ułamkowej

23 lis 11:49
aniabb: a1/n = n√a
23 lis 11:50
diks: X = 2√1/4
23 lis 11:52
pigor: ... , no to podsumowując, może spodoba ci się np. tak :
−2log24x+3log4x−1 >0 i
x>0 ⇒ −2log
24x+2log
4x+log
4x −1 >0 ⇔
⇔ −2log
4x(log
4x−1)+1(log
4x−1) >0 ⇔
−2 (log4x−1)(log4x−12) >0 ⇔
⇔
12< log
4x< 1 ⇔
√4< x < 4
1 ⇔
2< x <4 ⇔
x∊(2 ;4) . ...

23 lis 11:52
diks: pigor uwielbiam Cie za Twoje krótkie rozwiązania

ale niewiem czy zdąże się ich nauczyć..
przed jutrem.. nie mówiąc, że ide do pracy po południu

23 lis 11:54
diks: jak zwykle pigor wyszło Ci dobrze

23 lis 11:57
diks: jednak tam jest −1/2 a nie 1/2
23 lis 11:57
aniabb: to tego że minus przez minus daje plus jeszcze nie zauważyłeś

23 lis 11:59
diks: czyli x> 2p{1/4} i x < 4
23 lis 12:00
diks: czyli x > √4 i x < 4
23 lis 12:01
diks: czyli x∊(2,4)
23 lis 12:02
diks: 
23 lis 12:02
aniabb: 
23 lis 12:04
diks: następny:
log3xx −7log22x + 14log2x − 8 > 0
23 lis 12:06
diks: tam jest log
32x na początku

23 lis 12:07
diks: x>0 (0,+∞)
23 lis 12:08
diks: log2x = t
23 lis 12:08
diks: t3 − 7t2 + 14t − 8 > 0
23 lis 12:09
diks: t(t2−7t) + 2(7t − 4) > 0
23 lis 12:10
diks: (t2 − 7t)(7t−4)(t+2) > 0
23 lis 12:11
aniabb: z pierwszych dwóch t2 przed nawias
23 lis 12:20
aniabb: a nie nie pogrupujesz.. Hornerem
23 lis 12:21
23 lis 12:22
aniabb: (t−1) przed całość

(t−1)(t
2−6t+8) >0
23 lis 12:23
diks: o matko.. niewiem o co chodzi

23 lis 12:25
aniabb: taki fajny sposób na wyższe potęgi

23 lis 12:25
diks: Δ=b2 −4ac
Δ=(−6)2 −4*1*8
Δ=36−32
Δ=4
√Δ = 2
23 lis 12:42
diks:
t1 = 4
t2 = 2
23 lis 12:46
diks: 2 < log2x < t
23 lis 12:46
diks: log2x > 2
x> 22
x> 4
23 lis 12:47
diks: log2x < 4
x < 24
x < 16
23 lis 12:48
diks: 16 > x > 4
23 lis 12:49
aniabb: jak ten węzyk u Ciebie wygląda

23 lis 12:50
aniabb: ten do t

23 lis 12:50
diks: mam 3 punkty: zaczynając od lewej: 1,2,4 i wężyk zaczynając od prawej rysuje od góry.
23 lis 12:54
diks:
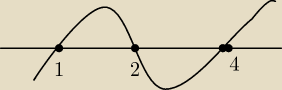
23 lis 12:57
diks: haha.. nauczyłem się rysować u Was

23 lis 12:57
diks: noi większe od zera czyli (1,2) i (4,+∞)
23 lis 12:58
diks: tylko mi się coś nie zgadza z odpowiedzią na końcu

23 lis 12:58
diks: aha......... węzyk będzie od dołu

23 lis 12:59
diks: bo przecież jak przemnoże przez siebie to będzie + t3 −6t2 itd..
23 lis 12:59
aniabb: no to teraz licz logarytm .. bo przed chwilą mi się zwroty nie zgadzały

23 lis 13:00
diks: w odpowiedzi jest że x∊(2,4) u (16,+∞)
23 lis 13:01
aniabb: jak masz + przed najwyższą potęgą to od góry
23 lis 13:01
diks: aha ja myślałem.. że to już koniec

23 lis 13:01
aniabb: a Ty na osi masz x czy t

23 lis 13:01
diks: no to dobrze.. ten węzyk jest narysowany?
23 lis 13:01
diks: t
23 lis 13:02
diks: log2x = 1
zatem x=2
23 lis 13:03
diks: tak więc mamy x1=2 x2 =4 i x3 = 16
23 lis 13:03
diks:
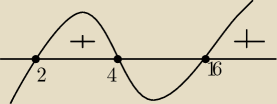
6
23 lis 13:05
diks: czyli x∊(2,4) u (16,+∞)
23 lis 13:05
aniabb: OK .. pasuje, bo podstawa większa niż 1

23 lis 13:07
diks: następny:
log31/3x − 3log21/3x − log1/3x + 3 < 0
23 lis 13:07
diks: x>0, dziedzina: (0,+∞)
23 lis 13:08
diks: log1/3x = t
23 lis 13:09
diks: t3 − 352 − t + 3 < 0
23 lis 13:09
diks: t3 − 3t2 − t + 3 < 0
23 lis 13:09
aniabb: z pierwszych dwóch t2 przed nawias
23 lis 13:16
diks: t2(t−3) −t+3 < 0
23 lis 13:22
aniabb: a z drugich −1 żeby w OBU nawiasach TO SAMO był
23 lis 13:26
diks: t2(t−3)−1(t−3) < 0
(t−3) (t2−1) < 0
23 lis 13:30
aniabb: i zamiast delty wzór skróconego mnożenia widzisz może

23 lis 13:31
diks: nieee widze

!
(a−b
(a+b) = a
2 − b
2?

23 lis 13:32
diks: Δ=b2 −4ac
Δ=0−4*1*(−1)
Δ=4
√Δ=2
23 lis 13:35
aniabb: tak ten

23 lis 13:37
23 lis 13:46
diks:
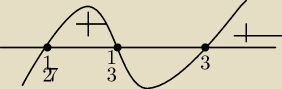
23 lis 13:50
diks: log1/3 = t1
log1/3 = 1
x= (1/3)1
x=1/3
23 lis 13:52
diks: log1/3 = t2
log1/3 = −1
x=(1/3)−1
x=3
23 lis 13:53
diks: log1/3 = t3
log1/3 = 3
x=(1/3)3
x=1/27
23 lis 13:54
diks: mamy (t−3) (t2−1) < 0 −−> jest mniejsze od zera
23 lis 13:55
diks: zatem x∊(−∞,1/27) u (1/3 , 3)
23 lis 13:55
diks: niestety w odpowiedziach na końcu wychodzi, że x∊(1/27,1/3) u (3, +∞)
23 lis 13:56
diks: więc gdzie jest błąd

23 lis 13:57
diks: chyba w wężyku.. ale przecież t3 jest dodatnie
23 lis 13:57
Aga1.: (t−1)(t+1)(t−3)<0
gdy t<−1 lub 1<t<3
i teraz log
1/3x<−1
x>3 lub
1<log
1/3x<3⇔
log
1/3x<3 i log
1/3x>1
tzn.
x∊(1/27,1/3)
Łącząc te dwie odpowiedzi wychodzi jak w podręczniku
23 lis 14:23
aniabb: mówiłam że wtedy nieświadomie odwrócileś ..a potem było dobrze bo akurat podstawa większa niż 1
23 lis 14:26
diks: O MATKO..
23 lis 18:40
diks: jest ktoś?

23 lis 18:43
konrad: jest ktoś

23 lis 18:44
diks: hehe

to super.. robimy dalej?

23 lis 18:45
Piotr:
tylko sie skup !

23 lis 18:45
aniabb: jestem jakby co

23 lis 18:46
diks: no to co zbliżamy się do mojego kolosa wielkimi krokami.. jak myślicie dam rade?

23 lis 18:47
diks: teraz już zaczniemy robić przykłady do kolosa

23 lis 18:48
Piotr:
jak nie to dostaniesz manto !

23 lis 18:49
diks: log4√x + log√2x+log1/16x = −6
23 lis 18:50
diks: będziecie mi jeszcze pomóc... dziś nie śpie całą noc

23 lis 18:50
diks: tak więc... tak ja bym tu zaczął od zamiany pierwiastka z x, a następnie zmienił podstawy z
liczbami logarytmowymi

23 lis 18:51
diks: zatem...
log4x(1/2) + log√2x + log1/16x = −6
23 lis 18:52
konrad: a ja bym zaczął od wyznaczenia dziedziny

23 lis 18:52
diks: (1/2)*log4x + log√2x + log1/16x = −6
23 lis 18:53
diks: a no też prawda.. dziedzina x>0 i √x> 0
zatem to przedział x∊(0,+∞)
23 lis 18:53
23 lis 18:54
diks: | 1 | | 1 | | 1 | | 1 | |
| * |
| + |
| + |
| = −6 |
| 2 | | logx4 | | logx√2 | | logx1/16 | |
23 lis 18:56
diks: √2 = 2(1/2)
23 lis 18:57
diks: 4 = 22
23 lis 18:57
diks: 1/16 = 2−4
23 lis 18:57
diks: | 1 | | 1 | | 1 | | 1 | |
| * |
| + |
| + |
| = −6 |
| 2 | | logx22 | | logx21/2 | | logx2−4 | |
23 lis 18:58
aniabb: ok
23 lis 18:59
Grzesiek: diks skąd masz te zadania?

23 lis 18:59
diks: logx2 = t
23 lis 18:59
konrad: można też było podstawy zamienić na 2
nie wiem w sumie co łatwiejsze
23 lis 18:59
diks: z zestawu

23 lis 19:00
diks: | 1 | | 1 | | 1 | | 1 | |
| * |
| + |
| + |
| = −6 |
| 2 | | t2 | | t1/2 | | t−4 | |
23 lis 19:00
Grzesiek: mam dokładnie takie same zadania na studiach

23 lis 19:00
aniabb: odmień podstawy
23 lis 19:01
diks: | | 1 | | 1 | | 1 | |
|
| + |
| + |
| = −6 |
| | 2t2 | | √t | | (1/t)4 | |
23 lis 19:01
aniabb: POTĘGI przed logarytm
23 lis 19:01
aniabb: wrrrrrrrrrrrrrr a o 18:52 jeszcze umiałeś
23 lis 19:02
diks: kórde ciężko.. ale może innym sposobem..
23 lis 19:02
diks: haha ok!

23 lis 19:02
diks: | 1 | | 1 | | 1 | |
| + |
| + |
| = −6 |
| 4t2 | | (1/2)t | | −4t | |
23 lis 19:03
aniabb: normalnie będę bić ... nie ma tu jakiejś kulki z pejczem ...

23 lis 19:04
diks: | 1 | | 1 | | 1 | |
| + |
| + |
| = −6 |
| 4t | | (1/2)t | | −4t | |
23 lis 19:04
diks: hah

teraz chyba dobrze

23 lis 19:04
konrad: oj diks

23 lis 19:05
konrad: chociaż nie no, teraz jest ok
23 lis 19:06
aniabb: teraz ok .. pomnóż przez t

23 lis 19:07
Grzesiek: DIKS nie kombinuj tak

to zadanie można zrobić bez sprowadzania do t

23 lis 19:07
diks: haa wiedziałem!

23 lis 19:07
diks: TO JAK TO zrobić łatwo, szybko i przyjemnie?! przy okazji ze zrozumieniem

23 lis 19:08
diks: no dobra i teraz sprowadzam do wspólnego mianownika..
23 lis 19:08
diks: | 1*(1/2)t*(−4t) | | 1*4t*−4t | |
| + |
| + |
| 4t*(1/2)t*(−4t) | | 4t*(1/2)t*(−4t) | |
| | 1*4t*(1/2)t | |
|
| = −6 |
| | 4t*(1/2)t*(−4t) | |
23 lis 19:10
aniabb: miał odmienić.. ale jak się uparł

i to widzi... to niech już utrwala co umie
23 lis 19:10
aniabb: diks

23 lis 19:11
konrad: ło matko, ale kombinejszyn
23 lis 19:11
aniabb: po prostu pomnóż przez t obustronnie to co miałeś o 19:04
23 lis 19:12
diks: | −2t2 | | −16t2 | | 2t2 | |
| + |
| + |
| = −6 |
| −8t3 | | −8t3 | | −8t3 | |
23 lis 19:13
diks: | −2t2 | | −16t2 | | 2t2 | |
| + |
| + |
| = −6 /*(−8t3) |
| −8t3 | | −8t3 | | −8t3 | |
23 lis 19:13
konrad: ja to bym od razu przez 4t pomnożył
23 lis 19:14
Piotr:
biedny diks

23 lis 19:14
diks: −2t2 −16t2 +2t2 = 48t3
23 lis 19:15
diks: −16t2 = 48t3
23 lis 19:15
diks: −48t3 −16t2 = 0
23 lis 19:15
diks: t(−48t2−16t) = 0
23 lis 19:16
aniabb: niektórzy kochają liczyć

23 lis 19:16
diks: Δ=b2 −4ac
Δ=(−16)2 − 4*(−48)*0
Δ=256
√Δ=16
23 lis 19:17
23 lis 19:17
aniabb: t
2 przed nawias .. czy delta będzie

23 lis 19:17
konrad: 
23 lis 19:17
diks: | | 32 | |
t1 = U{16+16}{{2*(−48)} = |
| |
| | −96 | |
23 lis 19:18
diks: poddaje się. −.−
23 lis 19:18
diks: ogólnie jestem

ide coś zjeść..
23 lis 19:19
Grzesiek: DIKS napisać Ci jak to zrobiłem?
23 lis 19:19
diks: nom

23 lis 19:20
diks: Grzesiek a gdzie studiujesz?
23 lis 19:20
Grzesiek: AGH Kraków
23 lis 19:25
konrad:
to ja sobie pozwolę napisać jak ja bym to zrobił:
log
4√x + log
√2x+log
116x = −6
| 1 | |
| log4x + log√2x+log116x = −6 |
| 2 | |
| 1 | | 1 | |
| log2x + 2log2x− |
| log2x = −6 |
| 4 | | 4 | |
2log
2x=−6
log
2x=−3
2
−3=x
koniec

23 lis 19:25
diks: hahah czy ja z Tobą czasem nie siedze

?
23 lis 19:26
aniabb:
| 1 | | 1 | | 1 | |
| + |
| + |
| = −6 |
| 4t | | (1/2)t | | −4t | |
pierwszy i ostatni się skracają
log
2x=−3
x=1/8
23 lis 19:26
Grzesiek: być może

grupa 1 inż śr?
23 lis 19:27
diks: yes

!
23 lis 19:27
diks: umiesz to wszystko

?
23 lis 19:28
diks: ja się z tym męcze od dwóch tygodni

23 lis 19:29
Grzesiek: jaki ten świat mały

ucz sie ucz jutro i tak nie zdamy

log to jest pikuś w porównaniu do
trygonometrii

23 lis 19:29
Grzesiek: nie czaje tylko 2 przykładów z logarytmów i całej trygonometrii
23 lis 19:30
diks: haaa trygonometria jest spoko

!
23 lis 19:30
aniabb: Grzesiek skop mu kostki ode mnie ..pleaseeee

23 lis 19:30
diks: NO dobra ale ma być albo równanie albo nierówność logarytmiczna więc raczej nie bedzie tych
przykładów od r do y

23 lis 19:31
Grzesiek: aniabb nie ma sprawy

robiłeś przykłady np z potrojonym kątem α?
23 lis 19:34
diks: wtf?!

23 lis 19:34
diks: następny:
log8 + log x ≤ logx2 + log (6−x)
23 lis 19:35
diks: no to tak dziedzina to będzie przedział (0,6)
23 lis 19:36
Grzesiek: będą na pewno

cała kartka CHYBA ma być

samo rysowanie, wyznaczanie dziedziny i
przeciwdziedziny np arctg jest proste ale rób to w działaniach

23 lis 19:36
diks: bo 6−x >0
−x> −6
x< 6
23 lis 19:37
konrad: dziedzina ok
23 lis 19:37
diks: log8x ≤ log(x2(6−x))
23 lis 19:38
diks: log8x ≤ log(6x2−x3)
23 lis 19:38
konrad: log8x
23 lis 19:38
diks: 8x ≤ 6x2 − x3
0 ≤ −x3 + 6x2 −8x
23 lis 19:39
Grzesiek: wg mnie to jest najprostsze zadanie na tej kartce

23 lis 19:40
diks: x(−x2 + 6x −8) ≤ 0
23 lis 19:41
diks: Δ=b2 −4ac
Δ=(−6)2 − 4*(−1)*(−8)
Δ=36−32
Δ=4
√Δ = 2
23 lis 19:42
konrad: +8
23 lis 19:42
diks: | | −6 +2 | | −4 | |
x1 = |
| = |
| = 2 |
| | −2 | | −2 | |
23 lis 19:43
diks: czemu plus 8?

23 lis 19:44
Grzesiek: wszystkie znaki na odwrót

23 lis 19:44
diks: | | −6 −2 | | −8 | |
x2 = |
| = |
| = 4 |
| | −2 | | −2 | |
23 lis 19:44
diks: aha czyli 6x2 − x3 − 8x ≤ 0 /*(−1)
23 lis 19:45
Grzesiek: przeniosłeś na lewą strone i nie zmieniłeś znaków
23 lis 19:46
diks: −6x2 + x3 + 8x ≤ 0
23 lis 19:46
diks: ok czyli jeszcze raz..
8x ≤ 6x2 − x3
23 lis 19:47
diks: x3 − 6x2 + 8x ≤ 0
23 lis 19:47
diks: Δ=4
√Δ=2
x1= 4
x2=2
x3=0
23 lis 19:48
aniabb: nie przenosił tylko napisał odwrotnie i nie zmienił zwrotu nierówności
23 lis 19:48
diks:
23 lis 19:49
aniabb: teraz ok
23 lis 19:49
diks: czyli x∊(−∞,0> u <2.4>
23 lis 19:51
diks: ale ŻE DZiedzina to (0,6) więc x∊<2,4>
23 lis 19:51
diks: jest ok?

23 lis 19:51
aniabb: w końcu

23 lis 19:54
diks: następny:
lol(log x) + log(logx2 −1) = 1
23 lis 19:55
diks: log x > 0
logx2 − 1 > 0
logx2 > 1
23 lis 19:57
diks: a więc
log x2 = 1
2log x = 1 /:2
log x = 1/2
x = 101/2
x = √10
23 lis 19:58
diks: zatem x jest większe od √10
dziedzina: x∊(√10, +∞)?
23 lis 19:59
aniabb: pozostałe są większe więc niech będzie

23 lis 20:02
diks:

23 lis 20:04
aniabb: teraz ok

23 lis 20:04
diks: czyli to będzie dalej..
log [(log x) * (log x2 −1) ] = 1
23 lis 20:05
diks: log [(log x) * (log x2 −log x) ] = 1
23 lis 20:06
diks: log b = 1 ⇒ 101 = b ⇒ b = 10
23 lis 20:06
diks: zatem log [1* (log x2 −1 ] = 10
23 lis 20:07
diks: log x [2log x −1 ] = 10
23 lis 20:08
diks: log x = t
23 lis 20:08
diks: t*(2t − 1) = 10
23 lis 20:08
diks: 2t2 −t − 10 = 0
23 lis 20:09
diks: Δ=b2 − 4ac
Δ=(−1)2−4*2*(−10)
Δ=1+80
Δ=81
√Δ = 9
23 lis 20:10
diks: | | 1+9 | | 10 | | 5 | | 1 | |
t1 = |
| = |
| = |
| = 2 |
| |
| | 4 | | 4 | | 2 | | 2 | |
23 lis 20:11
23 lis 20:11
Grzesiek: wytłumaczysz dlaczego Ci wyszlo tak jak w poście z 20.06?
23 lis 20:13
diks:
10
212 = x
x = 10
5/2 = (10
5)
1/2 =
√105
√10*1000 =
√10 * 100
23 lis 20:13
Grzesiek: a sorry nic źle popatrzyłem

23 lis 20:14
diks: ja niewiem czy ja to dobrze robie

23 lis 20:14
diks: log x = t
log x = −2
23 lis 20:15
diks: √10 = 3,16..
√10 * 100 = 3,16 * 100 = 316 (pasuje)
23 lis 20:17
diks: Grzesiek tak masz?
23 lis 20:17
aniabb: dobrze
23 lis 20:20
Grzesiek: nie wiem czy to potęgowanie dobrze rozpisałeś

10
212
23 lis 20:20
diks: yes yes yes

!

23 lis 20:21
Grzesiek: ok dobrze

tylko to jest tak w przybliżeniu 316 a ta babka raczej nie daje odpowiedzi w
przybliżeniu tylko zazwyczaj jakieś normalne liczby jej wychodzą

23 lis 20:21
Grzesiek: ale może to jest wyjątek

23 lis 20:22
diks: log4[2log3[1+log2(1+3log2x)]] = 1/2
23 lis 20:23
diks: to jest dopiero jazda

!
23 lis 20:23
Grzesiek: to zadanie odpuściłem
23 lis 20:25
aniabb: banał .. o ile odpuścicie dziedzinę

23 lis 20:27
aniabb: w sumie rozwiązując za każdy razem sprawdzać czy dodatnie zamiast dziedziny

23 lis 20:27
aniabb: to są te łatwe od których zaczynałeś..
23 lis 20:28
diks: aha log
pa = b gdy a=p
b
23 lis 20:30
aniabb: bingo

23 lis 20:31
diks: 2log3[1+log2(1+3log2x)]] = 41/2
23 lis 20:31
diks: 2log3[1+log2(1+3log2x)]] = √4
23 lis 20:32
aniabb: i widać że dodatnie więc w dziedzinie

23 lis 20:33
diks: log3[1+log2(1+3log2x)]]2 = √4
23 lis 20:33
diks: [1+log2(1+3log2x)]]2 = 3√4
23 lis 20:34
diks: log2(1+3log2x)]]2 = 3√4 −1
23 lis 20:34
diks: log2(1+3log2x)]]2 = 32 − 1
23 lis 20:34
diks: log2(1+3log2x)2 = 9 − 1
23 lis 20:35
diks: log2(1+3log2x)2 = 8
23 lis 20:35
diks: (1+3log2x)2 = 28
23 lis 20:35
diks: (1+3log2x)2 = 256
23 lis 20:35
ZKS:
Próbuj pisać w jednym poście a nie co linijka to kolejny nowy post.
23 lis 20:36
diks: 12 +6log2x + (3logx)2 = 256
23 lis 20:36
diks: spooko ZKS

23 lis 20:37
diks: 1 +6log2x + 9(logx)2 = 256
1 +6log2x + 9(logx)2 − 256 = 0
9(logx)2 +6log2x −255 = 0
23 lis 20:38
diks: log 2x = t
23 lis 20:38
diks: 9t2 +6t − 255 = 0
Δ=b2 −4ac
Δ=62−4*9*(−255)
Δ=36+9180
Δ=9216
√Δ=96
23 lis 20:40
aniabb: trzeba było spierwiastkować obustronnie

(1+3log
2x)
2 = 256
1+3log
2x = 16
23 lis 20:40
aniabb: x=25
23 lis 20:40
diks: | | −6+96 | | 90 | |
t1 = |
| = |
| = 5 |
| | 2*9 | | 18 | |
| | −6−96 | | −102 | | 34 | | 17 | |
t2 = |
| = |
| = − |
| = − |
| |
| | 2*9 | | 18 | | 6 | | 3 | |
23 lis 20:42
diks: log2x = 5
25 = x
x=32
23 lis 20:43
diks: log2x= −17/3
2−17/3 = x
(1/2)17/3 = x
23 lis 20:44
aniabb: 
wstąpił do piekieł po drodze mu było

23 lis 20:44
aniabb: ujemne odpada
23 lis 20:45
diks: (1/217)1/3 = x
23 lis 20:46
diks: aaa to fajnie

!
23 lis 20:46
diks: CZYLI ROZWIĄZANIEM TEGO RÓWNANIA JEST X=32?

23 lis 20:46
Grzesiek: a mnie sie wydaje że trzeba było obustronnie wsadzić pod pierwiwastek o 20.34
i odpowiedź wychodzi x=2
23 lis 20:50
aniabb:
log4[2log3[1+log2(1+3log2x)]] = 1/2
2log3[1+log2(1+3log2x)] = 2 dodatnie //:2
log3[1+log2(1+3log2x)] = 1
1+log2(1+3log2x) = 3 dodatnie
log2(1+3log2x)=2
1+3log2x=4 dodatnie
3log2x=3
log2x=1
x=2
23 lis 20:50
Grzesiek: czyli mialem racje

23 lis 20:51
aniabb: trzeba było dawno temu podzielić przez 2 ..ale trudno było wyciągnąć
√4 
23 lis 20:51
diks: EHH..

23 lis 20:52
Grzesiek: będę za 10 minut
23 lis 20:53
diks: rzeczywiście macie racje

23 lis 20:55
diks: a teraz takie zadanie..
ile rozwiązań ma równanie ax
2 −2x + 1 = 0, gdzie a jest pierwiastkiem równania:
23 lis 20:57
diks: o co w tym chodzi?

23 lis 20:57
diks: może to po prostu policze

23 lis 21:00
diks: 3x>0
x>0
23 lis 21:00
aniabb: najpierw policz a czyli rozwiąż logarytmy
23 lis 21:00
Eta:
"dawno ,dawno temu, za górami za lasami"

23 lis 21:01
aniabb: a to już chyba było...
23 lis 21:01
diks: kórde różne podstawy i różne liczby logarytmowane

23 lis 21:02
Tom: musisz w log x policzyć i ci ma wyjsc ładne a xd wstawic do trojmianu i okreslic Δ

wtedy bd
0 1 albo 2 ^^ chyba ze z kw. ci sięwkradnie
23 lis 21:02
aniabb: ale łatwiej policzyć niż znaleźć

23 lis 21:03
23 lis 21:07
Grzesiek: było bo ja to wrzucałem

23 lis 21:08
diks: | | 3 | |
log3x |
| + (log3x)2 = 1 /*x |
| | x | |
log
3x3 + (log
3x)
3 = 1
log
3x3 + (log
3x)
3 −1 = 0
23 lis 21:08
aniabb: aha

a ja szukam w tym wątku

23 lis 21:09
23 lis 21:09
aniabb: diks

23 lis 21:10
diks: ok to wybaczcie.. ale sobie to przepisze

23 lis 21:11
diks: Aniula zastąpiłaś log3x literką t?
i moje pytanie dlaczego tam jest w mianowniku drugim 1+1/t?
23 lis 21:23
diks: a nie to chyba tylko mały bład bo dalej widze jest dobrze

23 lis 21:24
diks: ok czyli mamy na końcu
1−t+t−1)(t+1)2 = 0
23 lis 21:25
diks: 1−t+(t−1)(t+1)2 = 0
23 lis 21:25
diks: co z tym dalej

?
23 lis 21:26
diks: przemnożyć nawiasy czy liczyć delte z trzeciego nawiasu

?
23 lis 21:27
aniabb: (t−1)[(t+1)2−1]=0
(t−1)[(t+1−1)(t+1+1)]=0
23 lis 21:27
aniabb: wyciągnąć nawias..rozpisać ze wzoru.. i KAZDY NAWIAS ODDZIELNIE
23 lis 21:28
aniabb: t=1 lub t=0 lub t=−2
23 lis 21:29
diks: (t−1)(t*(t+2) = 0
(t−1)(t2+2t) = 0
t3+2t2−t2−2t = 0
t3−3t2−2t = 0
23 lis 21:31
aniabb: nie błąd tylko miałam logx3 a to jest 1/log3x czyli 1/t
23 lis 21:32
diks: t(t2−3t −2) = 0
23 lis 21:32
aniabb: no zabiję ...<załamka>
23 lis 21:32
aniabb: 
23 lis 21:32
aniabb: KAZDY NAWIAS ODDZIELNIE =0
23 lis 21:33
aniabb: ja kombinuję żeby było widać, że da się powyciągać nawiasy a on i tak wymnaża...
23 lis 21:33
konrad: 
23 lis 21:34
diks: Δ=b2 − 4ac
Δ=(−3)2 −4*1*(−2)
Δ=9+8
Δ=17
23 lis 21:34
diks: ok czyli jeszcze raz..
mam coś takiego
1−t+(t−1)(t+1)2 = 0
23 lis 21:37
diks: 1−t+(t−1)(t2+2t +1) = 0
23 lis 21:38
aniabb: i jeszcze 2−1 = −3
23 lis 21:38
diks: 1−t+(t3+2t2+t−t2−2t−1) = 0
23 lis 21:39
aniabb: godz. 21:27
23 lis 21:39
diks: 1−t+t3+t2−t−1=0
t3+t2−2t = 0
23 lis 21:40
diks: godzina 21:27
(t−1)[(t+1)2−1]=0
(t−1)[(t+1−1)(t+1+1)]=0
23 lis 21:41
aniabb: oki
23 lis 21:41
diks: t1 = 1
t2= 0
t3= −2
23 lis 21:43
diks: o to chodziło?

23 lis 21:43
aniabb: tak <ufff>
23 lis 21:44
Kejt: ktoś mi tu niedawno pisał, że będzie miej postów? a Wy znów do 1 000 dobijacie powoli

23 lis 21:44
aniabb: bo po zmianie postu zapomniał wszystko co się nauczył

23 lis 21:46
diks: log3x = 1
31 = x
x=3
log3x = 0
30 = 1
x=1
log3x = −2
3−2 = x
x=1/9
23 lis 21:47
diks: dobra czyli mam te 3 iksy i co dalej

> ?
23 lis 21:48
diks: każdy po kolei mam podstawić do tego równania?
23 lis 21:49
diks: ax2−2x+1 = 0
23 lis 21:49
aniabb: to są 3 różne a.... teraz policz iksy
23 lis 21:50
diks: a3
2−2*3+1=0
a9−6+1 = 0
9a −5 = 0
9a = 5 /:9
23 lis 21:50
aniabb: ile rozwiązań ma równanie ax2 −2x + 1 = 0, gdzie a jest pierwiastkiem równania: log...
23 lis 21:51
Piotr:


23 lis 21:53
diks: Piotrze pomógłbyś.. a nie dobijał

23 lis 21:53
Piotr:
policzyles a

a wstawiasz za x

pisalem bys sie skupil.
23 lis 21:54
diks: aha

!
23 lis 21:55
aniabb:
1. 3x
2 −2x + 1 = 0,
2. 1x
2 −2x + 1 = 0,
3. 1/9x
2 −2x + 1 = 0,
i Twoja ukochana delta

23 lis 21:56
diks: 3x2 −2x +1 = 0
23 lis 21:56
Grzesiek: hehe widze że już chyba Ci sie gotuje

23 lis 21:58
diks: 1) Δ=−8
23 lis 21:58
aniabb: więc ile rozwiązań

23 lis 21:59
diks: 2) Δ=0 xw=1
23 lis 21:59
23 lis 22:01
aniabb: masz tylko liczbę rozwiązań podać .. wystarczy sama Δ
23 lis 22:02
Grzesiek: skoro jest Δ >0 to masz 2 rozwiązania czyli to równanie ma łącznie 3 rozwiązania

23 lis 22:04
diks: 1) zero rozwiązań
2) jedno rozwiązanie
3) dwa rozwiązania
razem 3 rozwiazania..
23 lis 22:04
Grzesiek: teraz sie dowiedziałem, że mają być równania i nierówności z zadania 1 (łącznie z trygonometrią
oraz wykresy funkcji cyklometrycznych i złożenia funkcji g o f

23 lis 22:07
diks: trygonometria to te sinusy cosniusy z tego pierwszego zadania

23 lis 22:09
diks: cos x − cos 3x = sin x − sin 3x
23 lis 22:10
Grzesiek: tak dokładnie... robimy je tutaj?
23 lis 22:10
diks: Aniula co tu się robi

?
23 lis 22:10
diks: róbmy

za 12 godziny będziemy pisać

23 lis 22:11
23 lis 22:12
diks: cos x − sin x = cos 3x − sin 3x
23 lis 22:12
Grzesiek: noo dobra nowy temat czy w tym?
23 lis 22:12
aniabb: rozwiązać pierwszy czy dacie radę ?
23 lis 22:13
diks: nowy temat

23 lis 22:13
Grzesiek: Ania żeby to było takie łatwe

23 lis 22:13
diks: Grzesiek czy ty też po raz pierwszy widzisz te wzory

? !
23 lis 22:14
Grzesiek: widziałem je już jak przeglądałem tą strone

to są wzory między innymi na sinus potrójnego
kąta to co mówiłem

23 lis 22:16
diks: | | α+β | | β−α | |
cos α − cos β = 2sin |
| * sin |
| |
| | 2 | | 2 | |
23 lis 22:17
aniabb: i drugi

23 lis 22:18
diks: | | x+3x | | 3x−x | |
cos x − cos 3x = 2sin |
| * sin |
| |
| | 2 | | 2 | |
23 lis 22:19
Grzesiek: ok czyli robimy

tylko my w zadaniu nie mamy kątów tylko x a nie wiem czy to też w ten sposób

bo mamy cos x − cos 3x = sin x − sin 3x
23 lis 22:20
23 lis 22:20
Grzesiek: tak i z tego wychodzi 2sin2x * sinx
23 lis 22:22
diks: kórde chyba coś pomyliłem ten wzór

23 lis 22:22
ZKS:
Można to trochę inaczej zrobić.
| | 1 | |
cos(x) − sin(x) = cos(3x) − sin(3x) / * |
| |
| | √2 | |
| | π | | π | | π | | π | |
cos(x)cos( |
| ) − sin(x)sin( |
| ) = cos(3x)cos( |
| ) − sin(3x)sin( |
| ) |
| | 4 | | 4 | | 4 | | 4 | |
| | π | | π | |
cos(x + |
| ) = cos(3x + |
| ) |
| | 4 | | 4 | |
| | π | | π | |
3x + |
| = x + |
| + k * 2π |
| | 4 | | 4 | |
23 lis 22:23
Grzesiek: dlaczego? dobrze

chyba

23 lis 22:24
ZKS:
Wykorzystany wzór to:
cos(x)cos(y) − sin(x)sin(y) = cos(x + y).
23 lis 22:24
aniabb: x czy α to nie ma znaczenia

23 lis 22:24
Grzesiek: yyyy co?

23 lis 22:25
aniabb: diks..ok ..
23 lis 22:25
diks: | | α−β | | α+β | |
sinα − sinβ = 2sin |
| * cos |
| |
| | 2 | | 2 | |
23 lis 22:27
Grzesiek: powiem Wam, że mnie to przerasta... 5 lat nie miałem matematyki...
23 lis 22:27
diks: | | x−3x | | x+3x | |
sinx − sin 3x = 2sin |
| * cos |
| |
| | 2 | | 2 | |
23 lis 22:28
diks: a ja miałem podstawową.. z której na lekcji był jeden wzór z logarytmu

tu się przez 2
tygodnie nauczyłem więcej niż przez 3 lata w liceum

23 lis 22:29
23 lis 22:30
aniabb:
cos x − cos 3x = sin x − sin 3x
2sin2xsinx = 2sin(−x)cos2x
sin2xsinx = −sinxcos2x
sin2xsinx + sinxcos2x=0
sinx (sin2x+cos2x)=0
23 lis 22:30
diks: 2sin−x * cos2x
23 lis 22:30
aniabb: ZKS miał lepszy sposób

23 lis 22:32
Grzesiek: Aniabb coś za łatwo Ci to wyszło

23 lis 22:32
Grzesiek: ale skąd u niego wzięło się π?
23 lis 22:33
diks: jak ja widze k i π to mi nie dobrze
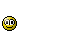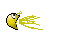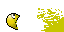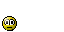
23 lis 22:35
diks: no dobra czyli mamy taką postać teraz..
sinx (sin2x+cos2x)=0
23 lis 22:35
ZKS:
Grzesiek jakie π?
23 lis 22:37
diks: czyli za x podstawimy k*π
23 lis 22:37
Grzesiek: sinx = 0 dla π2K tak?
23 lis 22:37
diks: czyli sinx = 0
23 lis 22:37
Grzesiek: | | π | |
Cos( |
| ) skąd to się wzieło? |
| | 4 | |
23 lis 22:38
aniabb: u ZKS cosπ/4 = sinπ/4 =√2/2
23 lis 22:38
ZKS:
Na pewno wiecie (oczywiście
aniabb wiadomo że wie

) że
| 1 | | π | | π | | π | |
| = sin( |
| ) = cos( |
| ) bo |
| = 45o. |
| √2 | | 4 | | 4 | | 4 | |
23 lis 22:39
diks: sin2x+cos2x=0
sin2x = −cos2x
23 lis 22:40
Grzesiek: | | 1 | |
teraz już wiem  ja szybko kumam  pomnożone jest przez |
| bo przy kącie 45 stopni sin |
| | p2 | |
= cos tak?
23 lis 22:40
23 lis 22:41
Grzesiek: tam miało być √2
23 lis 22:41
konrad: o, funkcje trygonometryczne... ja też tego nie lubię

23 lis 22:42
ZKS:
Bez argumentu sinus i cosinus nie mają sensu więc powinieneś poprawić zapis i zapisać
sinus oraz cosinus dla kąta 45o mają taką samą wartość.
23 lis 22:43
diks: | | π | |
cos( |
| −2x) = cos(π −2x) |
| | 2 | |
NIE!
23 lis 22:43
aniabb:
sinx=0 lub sin2x+cos2x=0
sinx=0 lub cos2x = − sin2x
cos2x = sin(−2x)
cos2x = cos(π−2x)
2x=π−2x +2kπ
4x=π +2kπ
x=π/4+kπ/2
23 lis 22:44
Grzesiek: aniabb cos jest przesunięty względem sin o π tak? dlatego w nawiasie pojawilo sie π? i drugie
pytanie dlaczego po usunięciu funkcji cos pojawiło się tylko z jednej strony +2kπ?
jestem bardzo kiepski z trygonometrii...
23 lis 22:47
aniabb: bo to cykliczność tu obojętnie do której
23 lis 22:51
diks: A SKĄD wiecie że to jest kąt 45 stopni a nie naprzykład 30 stopni

?
23 lis 22:52
diks: chodzi mi o to czemu ZKS pomnożył przez 45 stopni (π/4) a nie naprzykład przez 30 stopni>?
23 lis 22:52
Grzesiek: pomnożone jest przez 45 stopni bo wartość cos i sin przy kącie 45 stopni jest taka sama
23 lis 22:53
diks: czemu mnoże przez (π/4) a nie naprzykład przez (π/6)?
23 lis 22:54
aniabb: bo akurat jest równy i można mnożąc przez jedną liczbę dopisywać i sin i cos zależnie od
porzeby
23 lis 22:54
diks: aa rozumiem

23 lis 22:54
Grzesiek: | | √3 | | 1 | |
bo przy 30 stopnia wartość cos wynosi |
| a sin |
| |
| | 2 | | 2 | |
23 lis 22:54
diks: z drugiej linijki sin(−2x) zrobiłaś nagle w trzeciej linijce coś takiego Aniu cos(π−2x)?
o co chodzi? możesz wytłumaczyć

23 lis 22:55
ZKS:
Grzesiek nie używaj zapisu sin oraz cos bo w matematyce coś takiego nie istnieje.
23 lis 22:55
diks: wiem już o co chodzi Grześ

spojrzałem na tabelke

23 lis 22:56
Grzesiek: | | π | |
Aniabb a tam zamias π nie powinno być |
| ? bo przecież cos jest przesunięty nie o π tylko |
| | 2 | |
23 lis 22:57
aniabb: masz rację ..π/2
23 lis 22:57
diks: zatem co jest rozwiązaniem to co napisał ZKS czy to co napisała Ania?

23 lis 22:57
Grzesiek: ZKS obiecuję poprawe

23 lis 22:57
ZKS:
Powinno zwykła literówka.
23 lis 22:58
Grzesiek: kilka godzin z trygonometrią i bym nadrobił ale niestety za mało czasu zostało...
23 lis 22:59
Grzesiek: ZKS na pewno

dobrze, że są tacy ludzi jak Wy bo jest się od kogo uczyć

23 lis 23:00
aniabb: raczej zmęczenie i hałas nad głową

u mnie jeszcze ten sinx=0 bo myślałam że sami
rozpiszecie

23 lis 23:00
ZKS:
diks funkcje trygonometryczne są funkcjami okresowymi więc rozwiązanie które
zaprezentowała
aniabb jest identyczne z rozwiązaniem moim. Okej dziekuję
Grzesiek.

23 lis 23:01
Grzesiek: sinx=0 dla sin(kπ) tak?
23 lis 23:02
diks: wytłumaczcie mi mam naprzykład
| | 5 | | π | | π | |
cos |
| = to dlaczego to się równa cos{π + |
| ) = cos− |
| (<−−− jaka jest metoda |
| | 4 | | 4 | | 4 | |
tego rozpisywania
23 lis 23:02
23 lis 23:03
diks: | | 7 | | π | |
albo naprzykład cos |
| π} = cos(2π− |
| )  |
| | 4 | | 4 | |
23 lis 23:04
ZKS:
Grzesiek tak sin(x) = 0 dla x = kπ.
23 lis 23:05
ZKS:
157498 tutaj wyjaśniłem wzory redukcyjne jak działają post z 2 października 21:45.
23 lis 23:08
Grzesiek: | | 8π | | π | | 7π | |
patrz 2π = |
| − |
| = |
| |
| | 4 | | 4 | | 4 | |
23 lis 23:09
Grzesiek: yyy troche źle zapisałem ale może będziesz wiedział o co chodzi
23 lis 23:12
diks: zróbmy coś takiego teraz
3 sin x = 2 cos2 x
23 lis 23:19
diks: 3 sin x − 2 cos2 x = 0
23 lis 23:19
aniabb: cos2x =1−sin2x podstaw
23 lis 23:20
aniabb: potem sinx = t i Twoja uroczaΔ

23 lis 23:20
diks: 3 sin x − 2 (1−sin2 x) = 0
23 lis 23:21
diks: 3t −2(1−t2) = 0
2t2 + 3t −2 = 0
23 lis 23:22
ZKS:
Jeszcze założenie co do t ponieważ sinus przyjmuje wartości w zbiorze od [−1 ; 1] to
t ∊ [−1 ; 1].
23 lis 23:22
diks: Δ=b2 −4ac
Δ=32−4*2*(−2)
Δ=9+16
Δ=25
√Δ=5
23 lis 23:25
diks: stop źle!
23 lis 23:25
diks: t1 = 1/2
t2 = −2
23 lis 23:27
diks: sin x = −2
23 lis 23:27
diks: sin x = 1/2
23 lis 23:27
diks: i co ja teraz robie

?
23 lis 23:28
aniabb: albo odstawiając będzie widać w zapisie sinx=−2 że x∊∅

23 lis 23:28
aniabb: sinx=1/2 = sin π/3
x = π/3 +2kπ lub x = π−π/3 +2kπ
23 lis 23:30
diks: wiem, że x = π/6 + 2kπ lub x = 5/6π + 2kπ
23 lis 23:31
diks: aha ale sin x dla 1/2 to π/6 przecież

23 lis 23:32
aniabb:
23 lis 23:33
Grzesiek: diks ma racje 1/2 to 30 stopni

23 lis 23:34
aniabb: mówiłam żeście mnie już na maxa wymęczyli

23 lis 23:34
aniabb: też wolę stopnie niż Pi

23 lis 23:34
diks: Aniu przez dwa dni będziesz mieć spokój

23 lis 23:36
Grzesiek: diks i tak jest za późno żebyś się tego na jutro nauczył

23 lis 23:36
aniabb: och

dzięki ogromne

wyśpię się

i nie będę rozjeżdżać ludzi ( dziś) i
autobusów(ostatnio)

23 lis 23:38
diks: moze coś zostanie mi w głowie

23 lis 23:38
diks: powiedz mi Aniula o co chodzi z tym...
5
logx + 5
logx−1 = 3
logx+1 + 3
logx−1
| | logx | |
i teraz w drugiej linijce nasza profesorka dzieli {5logx}{5} przez 5 i 3 |
| dlaczego |
| | 3 | |
tak?
23 lis 23:41
diks: czyli jakby to −1 w tej potędze to jest ta piątka przez którą dzieli?

23 lis 23:42
diks: w drugiej linijce jest coś takiego:
| | 5logx | | 3logx | |
5logx + |
| = 3logx * 3 + |
| |
| | 5 | | 3 | |
23 lis 23:44
diks: 5logx (1+1/5) = 3logx (3+1/3)
23 lis 23:45
Piotr:
działania na potegach sie klaniaja.
| | 1 | | 2x | |
2x−1 = 2x * 2−1 = 2x * |
| = |
| |
| | 2 | | 2 | |
23 lis 23:45
diks: wiem, że jest wzór:
23 lis 23:46
aniabb: o właśnie

23 lis 23:47
diks: no ty Piotrze.. zawsze dodasz swoje 3 grosze.. akurat się sprzydały

23 lis 23:47
aniabb: ac to u Ciebie 51
23 lis 23:47
diks: ale super dziękuje wam bardzo.. za te dwa tygodnie już

23 lis 23:48
diks: rozumiem..bo normalnie myślałbym według tego wzoru że 5−1
23 lis 23:49
diks: ale Piotr mi fajnie to rozpisał

23 lis 23:49
Piotr:

23 lis 23:50
aniabb: już tyle <oooo> a Ty wciąż takie błędy robisz


23 lis 23:50
diks: no cóż... postaram się ćwiczyć.. chodź ostatnie dwa tygodnie to praca−dom−matematyka

23 lis 23:51
Piotr:
chcę jutro przeczytac, ze dobrze poszlo i czworka minimum bedzie

23 lis 23:52
diks: nierozumiem bo ten przykład jest zakończony tak..
i tak się zostawia takie równanie?

23 lis 23:52
diks: a pod spodem mi pisze.. funkcja wykładnicza jest różnowartościowa.
23 lis 23:53
aniabb: ja też

23 lis 23:53
aniabb: nie..porównujesz wykładniki woęc
logx=2
x=102 = 100
23 lis 23:54
diks: widze.. że Wam też już mózgi parują

!
23 lis 23:55
23 lis 23:55
diks: A SKĄD wiesz że log x =2?

23 lis 23:55
aniabb: tak jak znika logarytm tak znikają podstawy potęgi a dzieje się tak bo obie funkcje są
różnowartościowe
23 lis 23:56
Grzesiek: diks ja w zeszycie mam zakończone logx = 2

23 lis 23:56
aniabb: pamiętając przy nierównościach że podstawy ułamkowe zmieniają zwrot
23 lis 23:57
diks: aha czyli że potędze jest lox i po drugiej stronie jest w potędze dwójka
to obie potęgi równamy

!
HEEJ! ZAłapałem

23 lis 23:59
aniabb: 
23 lis 23:59
Piotr:
dziś piszesz kolokwium

23 lis 23:59
diks: ooo matko.. to już dziś!

!
24 lis 00:00
Piotr:
znowu czas sie nie zgadza

24 lis 00:00
Piotr:
test 00 : 03
24 lis 00:01
diks: Grześ jak tam przygotowany?

uczyłeś się?
24 lis 00:03
ZKS:
Trochę nie precyzyjnie powiedziane przepraszam że się czepiam
aniabb ale na przykład
| | 5 | | 5 | |
podstawą ułamkową jest |
| a przy nierówności ( |
| )x > 1 nie zmieniamy zwrotu |
| | 3 | | 3 | |
nierówności podstawa musi być w przedziale (0 ; 1) aby nierówność zmieniła zwrot na przeciwny.
24 lis 00:03
Grzesiek: aniabb w roli sprostowania podstawy ułamkowe >1 zmieniają (o ile sie nie mylę ?)

24 lis 00:03
Grzesiek: ucze się cały czas teraz uczę się g o f

jakoś idzie zobaczymy jutro na kolokwium zawsze
trudniej niż tutaj

24 lis 00:04
Grzesiek: KAWA SIĘ SKOŃCZYŁA CZAS SPAĆ

Dobrej nocy Wam życzę i miłej nauki

24 lis 00:06
diks: nie no to jest po prostu mistrzostwo odwracania Aniu!
3√3 = √9*√3 = √27 = √33 = (√3)3
24 lis 00:07
Piotr:
Witaj
ZKS 
Jak Siedem ?
24 lis 00:07
diks: wszystkie podstawy ułamkowe zmieniają znak nierówności...
24 lis 00:08
Piotr:
nie diks

przeczytaj post
ZKS .
24 lis 00:09
diks: czyli przy 1/2 już zmieniamy znak? bo to jest 0,5 i mieści się w (0,1)
24 lis 00:11
diks: tak

?
24 lis 00:12
aniabb: ułamki właściwe ..czyli góra mniejsza niż dół
24 lis 00:12
Piotr:
tak.
| | 4 | |
a np. |
| >1 wiec zwrotu nierownosci nie zmieniasz. |
| | 3 | |
24 lis 00:13
Piotr:
góra = licznik
dół = mianownik

24 lis 00:14
diks: dzięki piotrze... ale czemu na to mówimy podstawa? jak to przecież nie jest podstawa logarytmu
24 lis 00:16
diks: w tym przykładzie u nas konkretnym.. chyba że chodzi wam ogólnie?
24 lis 00:16
ZKS:
Witam
Piotr.

Świetny film ale końcówka to coś niesamowitego.

24 lis 00:17
Piotr:
bo to są podstawy potęg

24 lis 00:18
diks: aaaa rozumiem już

24 lis 00:18
aniabb:
potęga ab
a− podstawa potęgi
b− wykładnik potęgi
24 lis 00:18
ZKS:
Może znasz jakieś jeszcze dobre filmy?

24 lis 00:20
Piotr:
no pisałem, że końcówka jest niezła

24 lis 00:20
diks: DOBRA TO PDSUMUJMY nasze dwa tygodnie z logarytmami.. może wzorami..
24 lis 00:21
Piotr:
mnóstwo. Co Cie interesuje ?
24 lis 00:21
diks: 1) logab = c ⇔ ac = b
24 lis 00:21
24 lis 00:22
24 lis 00:22
diks: ahh piotrze ty zawsze masz na wszystko swoją stronę

24 lis 00:23
diks: no dobra to był głupi pomysł z tymi wzorami

24 lis 00:23
24 lis 00:24
Piotr:
nie no wypisz te co pamietasz

24 lis 00:25
24 lis 00:25
24 lis 00:26
Piotr:
aniabb 
24 lis 00:27
aniabb: i idę spać bo mi się paluszki plączą ...

no i cały czas trzymam kciuki

24 lis 00:27
diks: O MATKO...
narazie to ćwicze złożenie funkcji

24 lis 00:27
ZKS:
Napisz jakie byś filmy polecił jak coś powiem czy oglądałem czy nie.

24 lis 00:27
diks: tak a pro po
√x+1 ≥ 0 jak tu się wyznacza przeciwdziedzine?

?
24 lis 00:28
diks: √x+1 ≥ 0
x+1 ≥ 0
x ≥ −1
24 lis 00:29
aniabb: y∊<0;∞)
24 lis 00:29
diks: bo dziedzina to jest <−1,+∞)
24 lis 00:29
diks: ja wiem.. że tyle się równa.. aha bo pieriwastek może mieć najmniej zero tak:?
24 lis 00:30
diks: to już kapuje

24 lis 00:30
24 lis 00:30
diks: mam sporządzić wykres gof które mi wyszło |x+2| jak to się robi

?
24 lis 00:32
Piotr:
Ojciec chrzestny, Skazani na Shawshank, Zielona Mila, 12 gniewnych ludzi, Pluton, Lista
Shindlera, Piękny umysł ( z matematyka

), Dzień próby....
naprawde wiele gatunkow. nie wiem co lubisz

24 lis 00:32
aniabb:
24 lis 00:33
aniabb: rysujesz y=x+2 i wszystko co jest pod osią OX odbijasz na górę
24 lis 00:34
diks:
24 lis 00:34
aniabb: tak
24 lis 00:35
ZKS:
Pluton, Lista Schindlera, Piękny umysł , Dzień próby nie oglądałem także zaraz sobie pościągam.

24 lis 00:38
diks: a drugi mi wyszedł |x+1|
24 lis 00:40
Piotr:
może najpierw sprawdź sobie o czym są

24 lis 00:40
diks: zatem robie to samo tylko odbijam od punktu −1 i przechodzi mi przez 1
24 lis 00:40
diks: a jakby było |x−2|?

24 lis 00:41
Piotr:
12 gniewnych widziales ? jeden z moich ulubionych filmow. juz nie wiem ile razy obejrzalem

24 lis 00:42
Piotr:
aaaaa podałem tylko przykładowe

znam duuużo więcej

24 lis 00:43
diks:
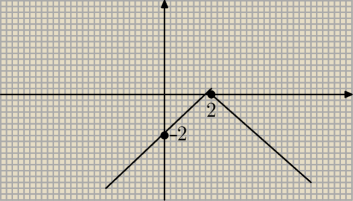
24 lis 00:44
Piotr:
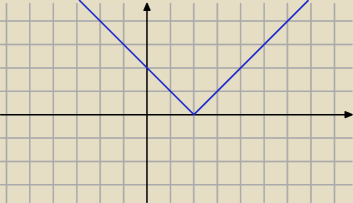
y = |x−2|
24 lis 00:45
ZKS:
Jakoś z tydzień temu oglądałem 12 gniewnych super film.

Sprawdziłem te pozostałe i wydają
się być bardzo ciekawymi filmami. To podawaj następne jak możesz.

24 lis 00:48
diks: czyli zawsze czy odejmowanie czy dodawanie wykres nie przebije osi OX

24 lis 00:48
diks: i zawsze rysujemu nad osią x, pod osią nigdy?

24 lis 00:48
Piotr:
wartośc bezwzgledna ≥ 0. sam sobie odpowiedz !

24 lis 00:50
diks: a jeżeli mam funkcje kwadratową w wartości bezwzględnej (parabola uśmiechnięta) to odbijam od
osi tylko ten uśmiech których przechodzi przez oś OX?
24 lis 00:52
diks:
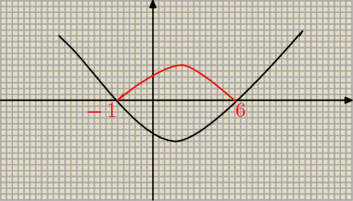
24 lis 00:55
Piotr:
ojej :
angielski tytul bo polski mi sie nie podoba : American History X
nie wiem czy lubisz westerny : W samo poludnie, Rio Bravo, Dobry zły i brzydki, Bez
przebaczenia
Tarantino polecam : Pulp Fiction, Wśiekłe psy
Olej Lorentza, Człowiek z blizną, Milczenie owiec, Chłopcy z ferajny, Nietykalni,
Ja np lubie stare filmy (polskie tez) wiec jak cos to pisz

24 lis 00:56
Piotr:
to co pod osia OX odbijasz do gory.
PS w rysowaniu funkcji mozesz tutaj użyc | | do wartosci bezwzglednej

24 lis 00:58
Piotr:
zeby bylo jasne NIetykalni z 1987r.
24 lis 00:59
ZKS:
Olej Lorentza i Nietykalni nie oglądałem westernów żadnych jeszcze nie oglądałem więc sobie
przejrzę i American History X również. Dziękuję bardzo.

24 lis 01:00
ZKS:
Tak myślałem że o ten Ci chodzi mam nawet nagrane ale jeszcze nie oglądałem. Ten co nie dawno
wyszedł oglądałem.

24 lis 01:01
Piotr:
nie ma sprawy

24 lis 01:02
diks: rozumiem.. że rozmawiacie o filmach by mnie odstresować..

niestety chyba Wam się nie uda

24 lis 01:03
Piotr:
i co ? faktycznie taki dobry jak pisza? bo mam z kolei ten nowy na kompie i jeszcze nie
obejrzalem

24 lis 01:04
Piotr:
@diks
kładź sie już, bo wszystko Ci sie pomiesza

również trzymam kciuki

24 lis 01:06
Piotr:
albo usniesz nad biurkiem i dopiero bedzie...

24 lis 01:06
ZKS:
Wiesz całkiem przyjemny ten film.

A Lot nad kukułczym gniazdem oglądałeś?

24 lis 01:08
Piotr:
pewnie. też dobry

24 lis 01:11
ZKS:
Incepcja , Gorączka , Zapach Kobiety , Życie Carlita?

24 lis 01:14
Piotr:
tylko incepcji nie widzialem. nie moge sie jakos zabrac do tego

24 lis 01:16
diks: jak wygląda w takim razie wykres jak jest |−x−1|

24 lis 01:16
ZKS:
|−x − 1| = |−(x + 1)| = |−1| * |x + 1| = |x + 1|
y = x następnie to co pod osią OX obijamy do góry dostajemy y = |x| później przesuwamy
w lewo o 1 jednostkę i mamy y = |x + 1|.
24 lis 01:19
Piotr:
Ludzie honoru, Kasyno, Gran Torino, Szeregowiec Ryan, Wyspa tajemnic, Nagle zeszłego lata, JFK,
Aż poleje sie krew, Mroczny rycerz... ?
24 lis 01:19
ZKS:
Mi się bardzo spodobała Incepcja ale to zacząłeś oglądać trochę i Cię nie zaciekawiło czy
jeszcze
nie zacząłeś?

24 lis 01:20
diks: yyy ok!

24 lis 01:22
ZKS:
Możesz pokazać co Ci wyszło.

24 lis 01:23
ZKS:
Tutaj to chyba tylko Mrocznego rycerza oglądałem a Aż poleje się krew mam na komputerze.

24 lis 01:26
Piotr:
kiedyś włączyłem ale mialem w zlej jakosci i po ok 15 min wylaczylem.
z opisu wydaje mi sie dobra ale jest dluga i sie jakos zrazilem

Dobra, ja ide spac. Dobrej nocy Wszystkim

24 lis 01:26
Piotr:
bardzo polecam jeszcze infiltracje ! naprawde dobry film !

24 lis 01:28
Piotr:
to zostało Ci duużo do obejrzenia

moze kolejny kinoman sie rodzi

24 lis 01:29
diks: ehh.. wam to dobrze

24 lis 01:33
ZKS:
Dobranoc

.

No trochę do obejrzenia jest jeszcze przede mną jeszcze raz bardzo
dziękuję
Piotr.

24 lis 01:38
diks: dołanczam się do podziękowań

ZKS Tobie też wielkie dzięki

24 lis 01:41
ZKS:
Mi to nie masz za co dziękować ale proszę bardzo i nie ma za co.

24 lis 01:44
diks: haha.. jest jest

24 lis 01:47
Grzesiek: i po kolosie

każdemu wyszedł inny wynik

24 lis 20:23
aniabb: woowww..zdolniście

24 lis 20:26
Grzesiek: pytałem się 4 osób i każdy miał inny wynik więc nie tylko my

jutro wszystko będzie jasne

24 lis 20:32
aniabb: to jak u nas na technologii organicznej..każdy miał inny wynik i każdy przekonany ze właściwy

a i tak ustny zaliczały tylko 2 osoby/sesję
24 lis 21:30
diks: noi zawaliłem logarytmy

Ania mam nadzieje.. że umiesz granice

! za dwa tygodnie kolejny
kolos

25 lis 21:10
diks: jaki głupi błąd zrobiłem.. zamiast 3 wspisałem sobie pod pierwiastkiem x.. niewiem dlaczego..
chyba ze stresu.. i dlatego mi nie chciało wyjść

życie jest okrutne..

25 lis 21:11
aniabb: 
umiem, umiem

damy radę

25 lis 22:12
Piotr:
buuu, tyle nauki

.
mam nadzieje, ze jednak zdales

26 lis 01:06
diks: no niestety nie zdałem

rysowanie arcusasinusa mnie wykończyło już totalnie po logarytmie

hehe.. to kiedy sie bierzemy za limesy


?!
26 lis 23:48
hihi: wow! thats cool
17 mar 17:59
17 mar 17:59
hihi: lemon−casino7.pl/promocode
17 mar 19:32

 najpierw dziedzina
potem że logpa > b to a>pb o ile p>1 jak mniejsze to zmiana znaku na przeciwny
najpierw dziedzina
potem że logpa > b to a>pb o ile p>1 jak mniejsze to zmiana znaku na przeciwny














 ?
?




 !
!


 ?
?

 zatem będzie x<1,5?
zatem będzie x<1,5? 







 x∊(2,5,1,5)
x∊(2,5,1,5)

 będę tak pisał
będę tak pisał 





 ?
?




 zatem.. (x−3)2>0
wzór skróconego mnożenia
zatem.. (x−3)2>0
wzór skróconego mnożenia x2−6x+9>0
x2−6x+9>0


 ?
?
 zatem dziedzina to (3 ; +∞)
zatem dziedzina to (3 ; +∞)



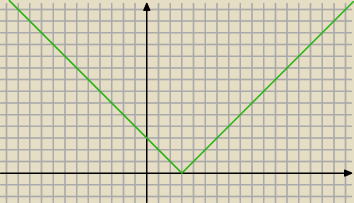 to jest wykres |x−3|
KIEDY |x−3| >0
to jest wykres |x−3|
KIEDY |x−3| >0 





 ?
?





 i będziemy działać
i będziemy działać 




 (x−3)2 > 1
x2 − 6x + 9 > 1
x2 − 6x + 8 > 0
(x−3)2 > 1
x2 − 6x + 9 > 1
x2 − 6x + 8 > 0




 ?
?



 ?!
?!






 x∊ <−11;7>
x∊ <−11;7>


 następne rób ładnie będę za godzinkę .. poczytaj linki
następne rób ładnie będę za godzinkę .. poczytaj linki
 następne rób ładnie będę za godzinkę .. poczytaj linki
następne rób ładnie będę za godzinkę .. poczytaj linki




 może z
może z  wyszedł
wyszedł 

 już jestem.. miałem korepetycje.. nie z majcy
już jestem.. miałem korepetycje.. nie z majcy 







 a jakie wyniki w książce ?
a jakie wyniki w książce ?
 ((((((((((((((((((((((((((
((((((((((((((((((((((((((


 ha !
ha !

 )
)




 2 msc zerowe! parabola itd
2 msc zerowe! parabola itd 

 spadam do pracy! narazie
spadam do pracy! narazie 

 poćwiczymy coś?
poćwiczymy coś? 


 √2 = 1,414213562
√2 = 1,414213562

 jesteś szalona
jesteś szalona  !
!

 czy wszystko jest ok?
czy wszystko jest ok? 
 ?
?

 !
!


 kiedy ten ZWROT żeś zmienił
kiedy ten ZWROT żeś zmienił 













 w tym tygodniu mam jakiś spadek formy
w tym tygodniu mam jakiś spadek formy 


 ?
?
 ?
?




 a jakbym podziedzlił przez siebie te logarytmy? bo w sumie to mają tą samą podstawe
a jakbym podziedzlił przez siebie te logarytmy? bo w sumie to mają tą samą podstawe 
 16−x2>0 dla x∊(−4,4)
16−x2>0 dla x∊(−4,4)

 MASZ racje
MASZ racje 

 log1/5(2x+1) − log1/5(16−x2) < −1
log1/5(2x+1) − log1/5(16−x2) < −1



 rzeczywiście lepiej ...
a równanka tak ładnie Ci szły
rzeczywiście lepiej ...
a równanka tak ładnie Ci szły 





 log1/2(5x+10) < log1/2(x2+6x+8)
5x+10 > x2+6x+8
−x2 −x +2 > 0
log1/2(5x+10) < log1/2(x2+6x+8)
5x+10 > x2+6x+8
−x2 −x +2 > 0




 (4−x) = 0 lub (2x−3) = 0
(4−x) = 0 lub (2x−3) = 0
 masz racje
masz racje 

 ładny
ładny 
 !
!
 jak policzyłeś deltę to masz iloczyn
2(x−3)(x+1)(4x−11) >0
taki wielomian wężykiem robimy ( rys)
jak policzyłeś deltę to masz iloczyn
2(x−3)(x+1)(4x−11) >0
taki wielomian wężykiem robimy ( rys)


 ok czyli będę wiedział.. że jak takie coś to wężyk..
ok czyli będę wiedział.. że jak takie coś to wężyk..

 chciałbym
chciałbym  !
!

 .
.
 Popraw dziedzinę, obliczenia w porządku.
Popraw dziedzinę, obliczenia w porządku.

 b>0
b>0










 odpowiedź do tej nierówności to: x∊(−3,−√6) u (√6,3)
odpowiedź do tej nierówności to: x∊(−3,−√6) u (√6,3)
 my tu mamy dwa logarytmy związane ze sobą 0.o
my tu mamy dwa logarytmy związane ze sobą 0.o





 x2 −5 >0 ⇔ x∊(−∞;−√5) u (√5; ∞)
x2 −5 >0 ⇔ x∊(−∞;−√5) u (√5; ∞)
 a teraz ostatecznie dziedzina
a teraz ostatecznie dziedzina 




 przetrwaliśmy
przetrwaliśmy







 ?
?

 OK
OK









 nie miales miec dzisiaj tego kolokwium ?
nie miales miec dzisiaj tego kolokwium ? 





 a ten tydzień to już prawie same nierówności
a ten tydzień to już prawie same nierówności 
 bo właśnie to zaczynam w
tą sobote...
bo właśnie to zaczynam w
tą sobote...


 ?!
?!
 !
!



 ćwicze i ćwicze
ćwicze i ćwicze 

 ?!
?!
 (jak było x2−22)
(jak było x2−22)


 !
!

 i nic więcej,
a można − nawet nie podając dziedziny (dlaczego ?) − np. tak :
i nic więcej,
a można − nawet nie podając dziedziny (dlaczego ?) − np. tak :



 jak smakowała
jak smakowała 





 ! JAK pozmieniałem? nie nie zmieniałem
! JAK pozmieniałem? nie nie zmieniałem 


 tye nauki
tye nauki 







 ?
?


 ale niewiem czy zdąże się ich nauczyć..
przed jutrem.. nie mówiąc, że ide do pracy po południu
ale niewiem czy zdąże się ich nauczyć..
przed jutrem.. nie mówiąc, że ide do pracy po południu 





 (t−1)(t2−6t+8) >0
(t−1)(t2−6t+8) >0











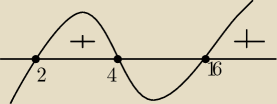 6
6


 !
(a−b(a+b) = a2 − b2?
!
(a−b(a+b) = a2 − b2?





 to super.. robimy dalej?
to super.. robimy dalej? 













 teraz chyba dobrze
teraz chyba dobrze 


 to zadanie można zrobić bez sprowadzania do t
to zadanie można zrobić bez sprowadzania do t 


 i to widzi... to niech już utrwala co umie
i to widzi... to niech już utrwala co umie






 ide coś zjeść..
ide coś zjeść..


 ?
?
 grupa 1 inż śr?
grupa 1 inż śr?
 !
!
 ?
?

 ucz sie ucz jutro i tak nie zdamy
ucz sie ucz jutro i tak nie zdamy  log to jest pikuś w porównaniu do
trygonometrii
log to jest pikuś w porównaniu do
trygonometrii 
 !
!


 robiłeś przykłady np z potrojonym kątem α?
robiłeś przykłady np z potrojonym kątem α?

 cała kartka CHYBA ma być
cała kartka CHYBA ma być  samo rysowanie, wyznaczanie dziedziny i
przeciwdziedziny np arctg jest proste ale rób to w działaniach
samo rysowanie, wyznaczanie dziedziny i
przeciwdziedziny np arctg jest proste ale rób to w działaniach 











 10212
10212
 !
! 
 tylko to jest tak w przybliżeniu 316 a ta babka raczej nie daje odpowiedzi w
przybliżeniu tylko zazwyczaj jakieś normalne liczby jej wychodzą
tylko to jest tak w przybliżeniu 316 a ta babka raczej nie daje odpowiedzi w
przybliżeniu tylko zazwyczaj jakieś normalne liczby jej wychodzą 

 !
!






 (1+3log2x)2 = 256
1+3log2x = 16
(1+3log2x)2 = 256
1+3log2x = 16
 wstąpił do piekieł po drodze mu było
wstąpił do piekieł po drodze mu było 
 !
!









 wtedy bd
0 1 albo 2 ^^ chyba ze z kw. ci sięwkradnie
wtedy bd
0 1 albo 2 ^^ chyba ze z kw. ci sięwkradnie


 a ja szukam w tym wątku
a ja szukam w tym wątku 




 ?
?
 ?
?





 > ?
> ?



 a wstawiasz za x
a wstawiasz za x pisalem bys sie skupil.
pisalem bys sie skupil.
 !
!






 ?
?
 za 12 godziny będziemy pisać
za 12 godziny będziemy pisać 


 ? !
? !
 to są wzory między innymi na sinus potrójnego
kąta to co mówiłem
to są wzory między innymi na sinus potrójnego
kąta to co mówiłem 

 tylko my w zadaniu nie mamy kątów tylko x a nie wiem czy to też w ten sposób
tylko my w zadaniu nie mamy kątów tylko x a nie wiem czy to też w ten sposób  bo mamy cos x − cos 3x = sin x − sin 3x
bo mamy cos x − cos 3x = sin x − sin 3x

 chyba
chyba 


 tu się przez 2
tygodnie nauczyłem więcej niż przez 3 lata w liceum
tu się przez 2
tygodnie nauczyłem więcej niż przez 3 lata w liceum 


 ) że
) że
 ja szybko kumam
ja szybko kumam  pomnożone jest przez
pomnożone jest przez 
 ?
?


 spojrzałem na tabelke
spojrzałem na tabelke 


 dobrze, że są tacy ludzi jak Wy bo jest się od kogo uczyć
dobrze, że są tacy ludzi jak Wy bo jest się od kogo uczyć 
 u mnie jeszcze ten sinx=0 bo myślałam że sami
rozpiszecie
u mnie jeszcze ten sinx=0 bo myślałam że sami
rozpiszecie 



 ?
?








 dzięki ogromne
dzięki ogromne  wyśpię się
wyśpię się  i nie będę rozjeżdżać ludzi ( dziś) i
autobusów(ostatnio)
i nie będę rozjeżdżać ludzi ( dziś) i
autobusów(ostatnio) 














 !
!


 !
HEEJ! ZAłapałem
!
HEEJ! ZAłapałem 


 !
!

 uczyłeś się?
uczyłeś się?

 jakoś idzie zobaczymy jutro na kolokwium zawsze
trudniej niż tutaj
jakoś idzie zobaczymy jutro na kolokwium zawsze
trudniej niż tutaj 
 Dobrej nocy Wam życzę i miłej nauki
Dobrej nocy Wam życzę i miłej nauki 
 Jak Siedem ?
Jak Siedem ?
 przeczytaj post ZKS .
przeczytaj post ZKS .
 ?
?

 Świetny film ale końcówka to coś niesamowitego.
Świetny film ale końcówka to coś niesamowitego. 




 https://matematykaszkolna.pl/strona/218.html
https://matematykaszkolna.pl/strona/218.html




 no i cały czas trzymam kciuki
no i cały czas trzymam kciuki 


 ?
?

 ?
?
 ), Dzień próby....
naprawde wiele gatunkow. nie wiem co lubisz
), Dzień próby....
naprawde wiele gatunkow. nie wiem co lubisz 






 znam duuużo więcej
znam duuużo więcej 

 y = |x−2|
y = |x−2|
 Sprawdziłem te pozostałe i wydają
się być bardzo ciekawymi filmami. To podawaj następne jak możesz.
Sprawdziłem te pozostałe i wydają
się być bardzo ciekawymi filmami. To podawaj następne jak możesz. 









 niestety chyba Wam się nie uda
niestety chyba Wam się nie uda 

 również trzymam kciuki
również trzymam kciuki 

 A Lot nad kukułczym gniazdem oglądałeś?
A Lot nad kukułczym gniazdem oglądałeś? 








 Dobra, ja ide spac. Dobrej nocy Wszystkim
Dobra, ja ide spac. Dobrej nocy Wszystkim 

 moze kolejny kinoman sie rodzi
moze kolejny kinoman sie rodzi 

 .
.  No trochę do obejrzenia jest jeszcze przede mną jeszcze raz bardzo
dziękuję Piotr.
No trochę do obejrzenia jest jeszcze przede mną jeszcze raz bardzo
dziękuję Piotr. 
 ZKS Tobie też wielkie dzięki
ZKS Tobie też wielkie dzięki 


 każdemu wyszedł inny wynik
każdemu wyszedł inny wynik 

 jutro wszystko będzie jasne
jutro wszystko będzie jasne 
 a i tak ustny zaliczały tylko 2 osoby/sesję
a i tak ustny zaliczały tylko 2 osoby/sesję
 Ania mam nadzieje.. że umiesz granice
Ania mam nadzieje.. że umiesz granice  ! za dwa tygodnie kolejny
kolos
! za dwa tygodnie kolejny
kolos
 życie jest okrutne..
życie jest okrutne.. 
 umiem, umiem
umiem, umiem  damy radę
damy radę 
 .
mam nadzieje, ze jednak zdales
.
mam nadzieje, ze jednak zdales 
 rysowanie arcusasinusa mnie wykończyło już totalnie po logarytmie
rysowanie arcusasinusa mnie wykończyło już totalnie po logarytmie  hehe.. to kiedy sie bierzemy za limesy
hehe.. to kiedy sie bierzemy za limesy 
 ?!
?!