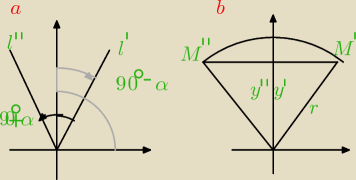
. asdf: Wzory redukcyjne: Końcowe ramiona tych kątów są półprostymi l' i l'' położonymi symetrycznie względem osi rzędnych. Współrzędne punktów M' i M'' leżących na tych półprostych tak, aby OM' = OM'' = r > 0 (rysunek b)) spełniają związki x'' = − x', y'' = y'. Stąd:

	y''		y'
sin(90o + α) =		=		= sin(90o − α) = cosα
	r		r

	x''		x'
cos(90o + α) =		= −		= −cos(90o − α) = −sinα
	r		r

Ja sobie tylko przepisalem, żebym miał czytelnie

ZKS: Wiesz jak mnie moja Pani z liceum nauczyła wzorów redukcyjnych?

asdf: Możesz powiedzieć, bo trochę mam z tym problemy − ale powoli ogarniam

asdf: Znam wierszyk itd, ale chcę te podstawy ogarnąć na 100%, żeby później nie kopać sobie dołu 'Kampania wrześniowa' i 'powstanie styczniowe' odpadają

Mila: Zapamiętaj definicje funkcji trygonometrycznych w układzie wsp. to bardzo pomaga w ustaleniu znaków i nie tylko. sin150=sin(180−30)=sin30 sin150=sin(90+60)=cos60 cos150=cos(180−30)=−cos30 cos150=cos(90+60)=−sin60 oblicz teraz na 2 sposoby sin120⁰ cos120⁰

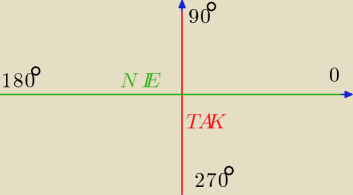
ZKS: Jeżeli wykorzystujesz kąty 90^o lub 270^o to tak jak głowa Ci idzie do góry i do dołu czyli kiwasz głowa tak jakby na "TAK" czyli wtedy przechodzisz na kofunkcje. Natomiast korzystając z kątów 180^o lub 360^o (zero) kiwasz głową na "NIE" jak na rysunku więc nie przechodzisz na kofunkcję czyli pozostawiasz daną funkcję. Przykład masz kąt α = 135^o sin(135^o) = sin(90^o + 45^o) tutaj kiwamy głową na "TAK" więc przechodzimy na kofunkcję i pamiętamy że sinus w drugiej ćwiartce jest dodatni cos(45^o). teraz cos(150^o) = cos(180^o − 30^o) kiwamy głową na "NIE" czyli nie przechodzimy na kofunkcję i pamiętamy że cosinus jest ujemny w drugiej ćwiartce −cos(30^o). Rozumiesz?

asdf: sin150 = druga ćwiartka, znak + sin(180 − 30) = parzysta wielokrotność, funkcja zostaje funkcją czyli: +sin30 sin120 = II ćw, zn: + = sin(90 + 30) = cos30 sin120 = sin(180 − 60) = sin60 cos120 = cos(90 + 30) = −sin30 cos120 = cos(180 − 60) = −cos60 dobrze?

asdf: To jeżeli to rozumiem nie muszę się bawić w to co w pierwszym poście ?

ZKS: Jeżeli chcesz możesz się bawić wybierz sposób który dla Ciebie jest najlepszy i tym rób.

asdf: Tylko mi coś nie pasuje napisałeś sin135^o = cos45^o, a według mnie: sin135 = sin(90 + 45) = −cos45 To ja już nie wiem....W tym przypadku patrzy się czy sinus jest dodatni, czy po zamianie na mniejszy stopień patrzy się na znak cosinusa?

ZKS: Masz przecież najpierw kąt w drugiej ćwiartce i jak zamieniasz na kofunkcję lub nie to wtedy dajesz plus albo minus. Rozumiesz?

Trivial: O nie nie.

	sinus w II dodatni mamy + 90o − kofunkcja
sin(90o + 45o) =		= cos(45o) = ...

ZKS: Trivial potwierdził że sin(135^o) = cos(45^o) a nie −cos(45^o).

asdf: czyli o 21⁴⁷ zrobiłem dobrze, a 9 minut później już źle ?

Trivial: tak.

asdf: To jak sobie obiorę taką drogę: 1^opatrze na f. trygonometryczną i kąt 2^o z wierszyka biore znak 3^o robię cofunkcje (TAK/NIE) 4^o wypisuje ZNAK + funkcja jaka wyszła + kąt tak?

Mila: Patrzymy na znak pierwszej funkcji , czyli sin135 =sin(90 + 45) = cos45 albo sin135=sin(180−45)=sin45

ZKS: Dokładnie. sin(225^o) zrób.

asdf: No to lajcik, taki mam przykład: tg1000^o = tg(4π + 280^o) = tg(280^o) <−−−−− wierszyk + znak (wyszedł dodatni) tg(270 + 10) = +ctg10^o

ZKS: Przecież sam piszesz 270^o + 10^o a to jest więcej niż 270^o więc jest to czwarta ćwiartka zły znak.

asdf: sin225 = sin(180 + 45) = C[znak ujemny −sin45^ lub: sin225 = sin(270 − 45) = −cos45 dobrze?

ZKS: .

asdf: A masz jakiś sposób na ogarnięcie wzorów: sin(x + y) cos(x + y) tg(x + y) ctg(x + y) sinx + siny cosx + cosy tgx + tgy ctgx + ctgy

ZKS: tg(687^o)?

asdf: tg687 = tg327 = ujemny tg327 = tg(360 − 33) = −tg33 tak też można? tg(327) = tg(−33) = −tg33

ZKS: A skąd Ci się wziął minus przy argumencie w drugim sposobie? Tak możesz robić tylko jeżeli bym podał Ci ujemny argument.

asdf: chciałem skorzystać, z: tg(−x) = −tgx, ale to przecież inny kąt Ja już nie myślę, 5 godzin snu i trochę siedzę przy tej matmie..Masz jakiś pomysł na ogarniecie tego co napisalem o 22¹⁹

Trivial: asdf, takie pytanko. Dlaczego akurat wzory redukcyjne?

ZKS: sin(x + y) oraz cos(x + y) łatwo zapamiętać a tg(x + y) możesz zapisać jak

sin(x + y)		sin(x)cos(y) + sin(y)cos(x)
	=		=
cos(x + y)		cos(x)cos(y) − sin(x)sin(y)

sin(x)cos(y)		sin(y)cos(x)
	+		=
cos(x)cos(y) − sin(x)sin(y)		cos(x)cos(y) − sin(x)sin(y)

sin(x)cos(y)
	+
sin(x)sin(y)   cos(x)cos(y)(1 −   cos(x)cos(y)

	sin(y)cos(x)
+		=
	sin(x)sin(y)   cos(x)cos(y)(1 −   cos(x)cos(y)

tg(x)		tg(y)
	+
1 − tg(x)tg(y)		1 − tg(x)tg(y)

Ale to chyba lepiej już się nauczyć.

asdf: @Trivial o to musisz spytać mojego wykładowcy

Trivial: Już was cisną? U mnie same zajęcia organizacyjne jeszcze (niewiele pracy).

Ajtek: Cześć Trivial, z pozostałymi się już dzisiaj witałem w innych wątkach. ZKS ten sposób na wzorki redukcyjne jest genialny .

Trivial: Cześć Ajtek. Jaki sposób?

Ajtek: Z kiwaniem głową. Nie słyszałem o nim wcześniej .

Trivial: Jest jeszcze inny sposób − zawsze sprowadzać do 180, 360. Żadnego kiwania głową.

asdf: @Trivial Ta, pierwsze cwiczenia, babka weszła, nazywam się .....Za duzo was tutaj.....Poziom matematyki spada od 20 lat....i po 3 minutach: "Zacznijmy od łatwych rzeczy" i się zaczęło 1,5h ćwiczeń

Ajtek: asdf ze smutkiem stwierdzam, że miała rację. Ale nie martw się, to "wietrzenie" Ciebie nie będzie dotyczyło, dasz radę .

asdf: Yhm...też tak myślę. Szczegolnie jak powiedziala "ludzi po maturze podstawowej z matematyki nie powinno tu być" Ale jak się uprę to się uda

Ajtek: Można i tak z π i 2π, ale to jednak nie jest pełne .

Trivial: asdf, miałeś już wykład z matmy, czy tylko ćwiczenia? U mnie kosmos był tylko na wykładach.

ZKS: Ajtek miałem w liceum świetną nauczycielkę i wiedziała jak trafić do uczniów niby takie głupie kiwanie głową a od razu wiadomo czy kofunkcja czy nie. Teraz zawsze robię tak jak Trivial napisał sprowadzam do 180^o lub 360^o.

asdf: Ćwiczenia przez 1.5 godziny. W tym semestrze mam: Analiza matematyczna i algebra liniowa bedzie ciekawie Co jest ciekawsze? Analiza czy algebra?

Ajtek: Analiza jest kozak, algebry liniowej jako takiej chyba nie miałem .

asdf:

Trivial: Zdecydowanie analiza. Algebra jest taka nieciągła... Nic nie zastąpi bardzo szybkiego pisania kredą po tablicy pasjonatki matematyki. Jeżeli będziesz miał slajdy to szczerze współczuję.

Aga1.: asdf, pamiętam pierwsze wykłady i ćwiczenia. Ledwo nadążyłam notować, a o zrozumieniu czegokolwiek na bieżąco nie było mowy. Jedną ręką pisali, a drugą natychmiast ścierali mówiąc, to trywialne. Na wykładach same definicje, twierdzenia i dowody. To był koszmar, nie to co teraz.

asdf: A z kąd wiesz jak jest teraz? To co dzisiaj miałem widziałem pierwszy raz na oczy, ale źle nie było...może dlatego, że wystarczy trochę usiąść by zrozumieć. Najlepszy był tekst wykładowcy: "Drodzy Państwo, ja poczucia humoru nie mam"

Trivial: skąd

Ajtek: Jak każdy dobry matematyk .

Święty: Byłem dzisiaj na wykładach i ćwiczeniach − tylko przez wczorajsze rozpoczecie plan sie tak niefortunnie ułożył, że ćwiczenia z algebry były przed wykładami. Facet z ćwiczeń wytłumaczył nam przez 20 minut tyle informacji ile wykładowca przez 2 godziny.

Aga1.: Sądzę , po zadaniach, które zamieszczają tutaj studenci (kiedyś granice, pochodne, całki były w każdej klasie liceum i technikum)

asdf: Bo teraz to jest tak: Chcesz umieć więcej − zdawaj rozszerzenie Chcesz robić co innego − wystarczy podstawa. Z jednej strony jest to dobre, bo po co humaniscie całki oznaczone, nie oznaczone, właściwe itd... Ja nie lubiałem czytać lektur − nie czytałem − zdałem podstawe i jakoś nie żałuję. Żałuję, że nie zdawałem rozszerzenia z matematyki − nauczycielka nie pozwoliła nie wiem czemu....

Trivial: what? nauczycielka nie pozwoliła? Przecież przedmioty wybiera się samemu.

Ajtek: Bo bała się słabego wyniku, dba o swoją opinię. Niestety to jest na chwile obecną norma: "Jak chcesz zdawać rozszerzenie, to ja Tobie udowodnię, że nie zdasz podstawy. Miesiąc gnębienia, pała za pałą i widzisz, nie umiesz podstaw, a za rozszerzenie chcesz się brać

asdf: Tak, rzeczywiście..bała się, a przed maturą powiedziała "nie wiedziałam, że ty tyle potrafisz". Czyli gdzie jest problem? W podejsciu nauczyciela i nie znaniu poziomu czy, ze "srala sie" o opinie? Za podstawe tez jest kazdy rozliczany. Do podstawy tez mozna nie dopuscic ucznia

Ajtek: Nie potrafię odpowiedzieć na to pytanie.

asdf: Nauczyciel jest od nauczania, uczen od uczenia sie. Juz nie bede pisac za czyje pieniadze nauczyciele maja na chleb i wakacje