Gustlik: Błędu nie widzę, ale taka ilość wzorów jest niemożliwa do zapamiętania. Natomiast o wiele łatwiej jest zapamiętać dwie reguły pozwalające na szybkie wyprowadzenie potrzebnego w danym zadaniu wzoru redukcjyjnego: pierwsza reguła to jeżeli kąt występujący na początku jest nieparzystą wielokrotnością kąta prostego 90 stopni np. 90 st. 270 st.), to funkcja zmienia nazwę na kofunkcję, a więc sinus przechodzi w cosinus, cosinus w sinus, tangens w cotangens, a cotangens w tangens. Jeżeli kąt jest parzystą wielokrotnością kąta prostego (np. 180 st., 360 st.), to funkcja nie zmienia nazwy. Druga reguła to ustalenie ćwiartki kąta (np. 90 st. + alfa to kąt ćw. II) w celu ustalenia znaku. Tu proponuję nauczyć się prostego wierszyka: W pierwszej wszystkie są dodatnie, w drugiej tylko sinus, w trzeciej tangens i cotangens, a w czwartej cosinus. Te dwie reguły wystarczą, zamiast wkuwania chyba ze 30 wzorów. Przykład: obliczyć sin 120 st.

	√3
sin 120 st. = sin (90+30) st. = cos 30 st. =		.
	2

Kofunkcja, bo mamy nieparzystą krotność kąta 90 st. na początku, a znak dodatni, bo 120 st. to kąt II ćwiartki, a "w drugiej tylko sinus" jest dodatni − tak wynika z wierszyka − znak ustalamy dla funkcji wyjściowej, a nie dla wynikowej, czyli w naszym przykładzie dla sinusa !. Przykład 2: Obliczyć tg 225 st. tg 225 st. = tg (180+45) st. = tg 45 st. = 1 Funkcja nie zmienia nazwy, bo mamy kąt 180 st., a więc parzystą krotność 90, a znak dodatni, bo 225 st. to ćwiartka III, a "w trzeciej tangens i cotangens" są dodatnie − tak mówi wierszyk.

Gustlik: Jest jeszcze jeden fajny wierszyk dotyczący funkcji kata ujemnego: Wiadomo, że: sin(−α) = −sinα tg(−α) = −tgα ctg(−α) = −ctgα ale: cos(−α) = cosα A więc: FUNKCJA COSINUS GUBI MINUS .

Baku: Wielkie dzięki Gustlik! Ta metoda pozwoliła mi nie tylko zminimalizować ilość wkuwanego materiału, ale wręcz w końcu zrozumieć trygonometrię! Oby więcej takich jak Ty

z II LO: Ahhhh Strona laduje w zakladkach Przyda sie i to bardzo

Enived: α∊(0;90) do wzorów redukcyjnych

fgh: może ktoś by dodał wzory na 360stopni

:)) Paulina: wzory na 360 sa rowne tym na 0

Jakub: Zgadza się Paulina. Z tego powodu, że 360^o jest okresem podstawowym funkcji sin i cos i podwojonym okresem podstawowym dla tg i ctg.

Gustlik: sin(k*360^o+α)=sinα cos(k*360^o+α)=cosα tg(k*360^o+α)=tgα ctg(k*360^o+α)=ctgα Jeżeli na początku występuje kąt 360^o lub jego wielokrotność, to mozemy ten kąt pełny skreślić i zostaje do obliczenia funkcja kąta α. Np.

	1
sin750o=sin(720+30)o=sin(2*360o+30o)=sin30o=		.
	2

Magda: a moze ktos jeszce napisac wiecej przykładów wg gustlika to jesajne, tylko chyba mi sie wydaje ze trzeba patrzec zeby odejmowac lub dodawac do π np.( 135=180−45) albo (225=180+45) bo wtedy nie ma zadnej kofunkcji i jak jest sin to nadal jest sin cos tg i ctg tak samo. ale właśnie bardzo mi zalezy o wytłumaczenie na podstawie kilku przykładach kofunkcji

Karolcia: A jeśli jest sin² 37^◯ to na to nie ma wzoru . wiec jak to obliczyć?

Mastah: Z czego wynika znak +/− we wzorach redukcyjnych tych w drugiej części?: sinα(90−α) = (tu) cosα ITD Prosiłbym o pomoc.

lili: no ok wszystko pięknie a jeśli mam obliczyć sin105st, czyli sin(45 + 60) ?

Jakub: Dokładnie lili. Robisz ze wzoru sin(α+β) = sinαcosβ + cosαsinβ na 1543. sin(105^o) = sin(45^o+60^o) = sin45^ocos60^o + cos45^osin60^o =

√2

1

√2

√3

√2

√6

√2+√6

=

*

+

*

=

+

=

2

2

2

2

4

4

4

mike: prosze o pomoc w zadaniu. narysuj wykres funkcji y=cos x ,dla x E <−1.5pi; 1.5pi> i na jego podstawie wyznacz te argumenty dla których funcja osiaga wartośc równą cos 150stopni.

Jakub: Wykres funkcji y=cosx masz na 427, a rozwiązywanie równań trygonometrycznych na 1578. Jak dalej sobie nie będziesz potrafił poradzić, napisz to zadanie na forum zadankowym.

Kamil: Zgadzam się z Gustlikiem. Nie ma co tyle wzorów wkuwać, to samo pomyślałem. I też podobne zależności zauważyłem.

ysiulec: Przystępniejsza forma wierszyka różni się pierwszym wersem: W pierwszej ćwiartce same plusy w drugiej tylko sinus w trzeciej tangens i cotangens a w czwartej cosinus

Gulasz: tego jest strasznie dużo nie dam rady nie zdam =(

Jakub: Kliknij "minimalny zestaw wzorów redukcyjnych" na poprzedniej stronie.

Magda: Hej, potrzebuje pomocy Jeżeli α jest kątem ostrym i sin α=2/3 to wartosc cos(90 stop. − α) jest równa

kali: Do czego tak naprawdę służą te wzory sin(−α),cos(−α),tg(−α),ctg (−α)? Kiedy np mogą się przydać , w jakiej sytuacji?

Jakub: Jak masz policzyć np. sin(−30^o) = −sin30^o = −¹₂

maturzysta: te wzory są w tablicach na maturze?////

Jakub: Tych wzór akurat nie ma, ale można je sobie wyprowadzić ze wzorów na 1543, które już są w zestawie wzorów maturalnych.

Spart: Ale za to w tablicach są wykresy funkcji sin, cos więc jak je rozumiesz to zastąpią Ci każdy wzór,.

aia: a jak rozwiązać sinus (α−90)

alojzy: Nie rozumiem jednego: dlaczego cos(90−α)=sinα? Wg mnie powinno być −sinα gdyż ja to rozumiem tak, że cos(90−α) jest to funkcja symetryczna do sinx wzgl. osi OX przesunięta o π/2 (90st.) w prawo. Czy i dlaczego moje rozumowanie jest błędne, skoro sprawdza się przy sin(90−α)=cosα

matti_94: Alojzy. cos(90−α)=sinα poniewaz z definicji wiemy ze sinus to y/r. Watrosci w pierwszej cwiartce (90−α) sa dodatnie, gdyz y>0 wiec y/r tez bedzie dodatnie. Jest to tzw zmiana fukcji na kofunkcje gdy operujesz na osi y czyli 90 i 270 stopni.

quarhodron: dlaczego sin(−a)=−sina a cos(−a)=cosa ? i dlaczego jest w ogóle −a ? kąt ujemny czy jak ?

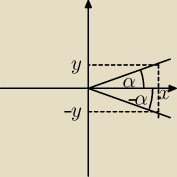
Jakub: To wynika z definicji funkcji trygonometrycznych, które masz na 417. Tak na szybko

	−y		y
sin(−α) =		= −		= −sinα
	r		r

	x
cos(−α) =		= cosα
	r

Widać to też na wykresach y = sinx (strona 426) i y = cosx (strona 427).

wojtus: sin(α−90) jak liczyć?

Jakub: sin(α−90^o) = sin[−(90^o−α)] = −sin(90^o−α) = -cosα

marcin: nie które zadania są trudne ale i też łatwe do zrobienia