MATURA P@weł: Jakie typy zadan z trygonometrii najlepiej powtorzyc do matury rozszerzonej ?

Marcin: równania trygonometryczne

kyrtap: równania z wartością bezwzględną lub nierówności , równania trygonometryczne , wykresy szczególnie te gdzie się bada w zależności od wartości parametru m liczbę rozwiązań, równania kwadratowe z parametrem tw. cosinusów i sinusów

P@weł: raczej wykazywanie tożsamości sie nie zdarza?

Marcin: W sumie to może się zdarzyć. Tylko nie wierzę, że CKE pokusiło by się na coś trudnego

P@weł: Szczerze powiedziawszy trygonometria to chyba moja pieta achillesowa Co byście polecili z tego mi powtorzyc? https://matematykaszkolna.pl/strona/3421.html tak jak patrze na te działy to tylko mi się rzuca w oko : https://matematykaszkolna.pl/strona/1578.html

razor: http://www.zadania.info/d62/1

kyrtap: koniecznie Paweł skup się na równaniach trygonometrycznych bo to zawsze jest

P@weł: kyrtap wlasnie tak patrze na matury i dochodze do wniosku ze zmarnowalem 2 dni na jakies pierdoły z trygonometrii , na tego typu zadania https://matematykaszkolna.pl/strona/1522.html Od chyba 2008 na każdej maturze bylo rownanie trygonometryczne

razor: Jakieś wybitne te równanie nie są na maturze Zazwyczaj jest zadanie albo na wyłączenie przed nawias albo zamiana sin²x na cos²x i sin2x cos2x na sinx i cosx

Tankian: Rownania trygonometrycznel. Tylko.

Tankian: Ew. do podstawienia pomocniczej niewiadomej

P@weł: Razor, racja tak jak mowisz

P@weł: dobra , dzieki za pomoc chłopy! lece porobic rownania

Marcin:

	1
Jak się pojawi na maturze np. sin(2x)=−		, to będzie panika że za trudne dali
	2

razor:

	3
Marcin spotkałem się już z takimi wybitnymi jednostkami, dla których jeśli tgx =		, to
	4

	sinx
sinx = 3, a cosx = 4. Dlaczego? Bo tgx =
	cosx

Marcin: Nie ma się co śmiać. Pół roku temu miałem podobne myślenie

razor: U mnie tak samo Pół roku temu napisałem rozszerzenie na próbnej na 12% i podstawę na 76 Dopiero to mnie trochę zmotywowało do nauki

P@weł:

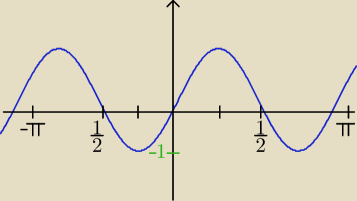
	π
odpowiedzia będzie x=
	4

Tylko czy + 2kπ czy + kπ ?

Marcin: No to ładnie się podszkoliłeś razor, nie powiem Teraz wymiatasz

razor: okres funkcji sin2x to π więc + kπ

razor: a nie nawet nie spojrzałem co napisałeś sin2x = −1/2

	π		7π
2x =		+ 2kπ lub 2x =		+ 2kπ
	6		6

jeszcze podzielić na 2 i jest

Marcin:

	1
Paweł odczytuj tak jak dla normalnego sinx=−		, tyle że później wynik podziel przez 2
	2

razor: no Marcin jeszcze jakby z fizyki mi tak szło jak z matmy

P@weł: Najlepsze jest to ze mature rozszerzona napisalem na 34% a w tej chwili te sama jestem w stanie napisac na 70% , to jest niefart ze szczescie ucieklo z przed nosa

Marcin: Fizykę rozszerzoną zdajesz?

razor: no niestety xD to będzie porażka, nic nie umiem

Marcin: Pozdro Paweł jak stwierdziłeś, że jesteś w tym momencie napisać tą samą maturę na 70%? Przecież jak już ją robiłeś, to bez sensu są takie stwierdzenia

P@weł: Marcin, moze masz w tych sporo racji, chodzi mi o to ze nie przyswoiłem materiał ktory przerabialem z korepetytorem, nie zrobilem zadania z funkcji kwadratowej za chyba 5/6pkt , zadania z rownosci trygonometrycznej, zle zrobilem zadanie z prawdopodobienstwa i jeszcze jakies tam , stracilem na tym ok 25pkt, poprostu nie rozumialem tych działow , teraz je rozumiem, ale sie obawiam ze moga sie nie powtorzyc podobne zadania....porażka jesli nie poprawie wyniku

Marcin: A ile chcesz mieć?

Hugo: 25 pkt w plecy to jest 50 % ;_; JA TEŻ LUBIE POGRAĆ W LOLA/TIBIE ALE BEZPRZESADY

P@weł: Chyba załapałem o co chodzi z tymi 2kπ i kπ jesli mamy np . sinx = −1

	1
to odpowiedzia będzie x =		π + 2kπ
	2

a jesli mamy sin(2x) = −1

	1
to: 2x=		π + 2kπ /: 2
	2

	1
x=		π +kπ
	4

kπ bez dwójki z przodu piszemy wtedy kiedys funkcja np cos. sin jest skórcona . prawda? kiedy okres jest krótsszy ? czyli gdy w zapisie występuje 2x np. sin(2x) = −1

Hugo: garniak + komórka do garniaka + kup se neta na dzień 2zł

P@weł: Hugo napisalem około DD wiec sie uspprawiedliwiam ±10 pkt hehehe

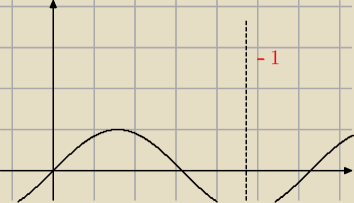
Hugo: YES ale ja ci powiem ... zawsze sb rysuj ! sinx=−1 x=3/2pi + 2kpi

Marcin:

	1
Paweł! Jesteś pewien, że sin(x)=−1, to x=		π?
	2

Hugo: co to dwojego sin(2x)=−1 to niby tak... ale głowy Ci nie dam czy to sie tak robiło bo f. sinus to nie f. liniowa ze jak podzielisz przez 2 to bedzie 2 razy mniejsze... Ale tu sie nie wypowiadam pewnie bym zrobił tak samo ale sam mam braki . Niech sie Marcin wypowie

Hugo: Marcin odnieś sie do mojego postu 1:50

P@weł: racja, z rysunku łatwiej odczytac

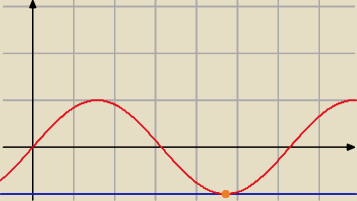
Marcin: Tak, tylko ze Paweł źle odczytuje w wykresu. Chyba ze nie odczytuje

P@weł: Marcin , ajjjjjjj byka walnalem tam powinno byc 1 zamiast −1

P@weł: dla sinx= 1

	1
x=		π + 2kπ
	2

Hugo: Paweł 50zł za lekcje u Huga albo somersby bo strasznie lubie

Marcin: No to wtedy tak sinx=1

	1
x=		π + 2kπ k∊C
	2

sin(2x)=1

	1		1
2x=		π + 2kπ / *
	2		2

	1
x=		π + kπ k∊C
	4

Macie rację

Hugo: Marcin ale tak można sin(2x)=1

	π
2x=
	2

	π
x=		?
	4

jesteś tego pewny?

P@weł: Hugo BTW jaki lvl w TIBII? hahahaha http://www.youtube.com/watch?v=Z7gdlKyuXGM

Marcin: ehee

Marcin: To tak zeby was sprawdzić

	3
sin(		x)=0
	2

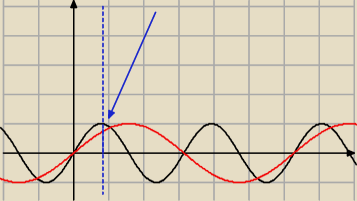
Hugo: mamy tu sin2x i sinx i to tak ładnie mi z rysunku nie wychodzi że 2x=π/2 ⇔ x=pi/4 ale ufam na słowo mądrzejszyś

Hugo: Paweł nie no ściema.. ale w Lola 17 .. Wot mam IX arta usa i IX is 8.. ale 2 mies przed maturami sb dałem formata na gry poszło 550 GB

Hugo: ...zło wróciło w nowym patchem

Hugo: z tw. Marcina sin(U{3]{2}x)=0

3
	x=2kπ
2

	4
x=		kπ
	3

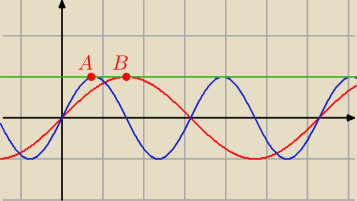
Marcin: Nie widzisz, ze punkt A, jest dwa razy blizej od osi OY?

P@weł: Hugo , nie wiem co znacza te nazwy tak tylko zapytalem o te gre bo wspomniales D A wracajac do rownania co napisal Marcin:

3		3
	x = π + 2kπ /*
2		2

	3
x =		π + 3kπ
	2

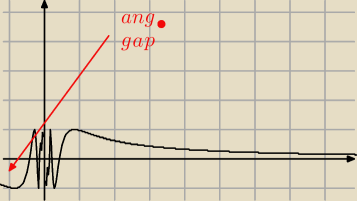
Hugo: #sin(3/2x) patrzcie co wyszło ! Praca serca Za początek cyklu pracy serca powszechnie przyjmuje się pauzę. W czasie pauzy przedsionki i komory serca są w stanie rozkurczu i krew pod wpływem gradientu (różnicy) ciśnień przelewa się z żył głównych i płucnych do przedsionków, a stamtąd do komór.

Hugo: Marcin: złudzenie optyczne . . . . ale jak by było takie na maturze to dopisze z tw. Marcina i podam gdzie mieszkasz

Marcin:

	3		3
Paweł! Ile to jest		*		?
	2		2

Marcin: Hugo, gdzie mieszkam?

P@weł: ojj powinno tam byc dzielenie.......... ale zepsułem

P@weł: Marcin a tak poza tym to chyba i tak w "4 maj 2014 02:08" mam bład bo nie powinienem chyba pisac : π + 2kπ ?

Hugo: Tymczasowo twoja lokalizacja to zmienna #Gdzieś . . . mógłbym odpalić Backtracka poszperać po forach i może bym coś po IP z twoich wspisów z tego forum jakoś na nielegalu z podsieci twojego HOSTERA wyczaił IP właściwe a potem do map google Kordy i Cie mam !

Hugo: Marcin mam rozkmine https://matematykaszkolna.pl/forum/249064.html

Marcin:

	3
sin(		x)=0
	2

3		2
	x=kπ / *
2		3

	2
x=		kπ k∊C
	3

Marcin: Hugo moja lokalizacja przez IP nic Ci nie powie. Obecnie wg. takiego sprawdzania jestem w Warszawie Szerokość geograficzna:52.2298 Długość geograficzna:21.0118

Marcin: Hugo! Lorak Ci pomaga

Hugo: fu!k zrobiłem dla okresu 2pi ... przyjmijmy że był to cos(3/2x) =1

Hugo: NEIN to ci podaje.. tzn nie wiem co i jak robisz ale to ci podaje IP usługodawcy.. ja mam z NEtii z Mysłowic Ale wiem ze da sie jakos inaczej

Marcin: Da się, ale na pewno nie tak prosto jak Hugo myśli

P@weł:

	3
Marcin w tym sin(		x) = 0
	2

to wychodzi kπ dlatego ze miejsce zerowe jest co kπ gdzie k nalezy do liczb C

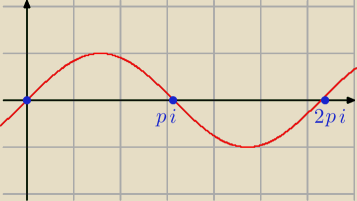
Marcin: Tak jak piszesz

Hugo: kryzys zażegnany TAM

Marcin: Tak na przyszłość, to lepiej podstawiaj za y, a nie za x

Hugo: Marcin do której siedzisz? .. ja dobrze podstawiłem za'y' ale po prostu sie pytałem

Marcin: Nie idę dzisiaj spać wcale

P@weł: MAsz rację bedziesz mi pomagał HOHOHO !

Hugo: Szkoda zeszytu robie zwami wyznacz wszystkie wartosci parametru m dla których równanie x²−(m−4)x+m²−4m=0 ma dwa różne pierwiastki rzeczywiste których suma jest mniejsza od 2m²−3 //porażka OKE ale cóz.. Hugo przynajmniej bedzie mieć pkt x²−(m−4)x+m²−4m=0 x₁+x₂<2m²−3 Δ>0 Δ=(−(m−4))²−4(m²−4m) Δ=m²−8m+16 − 4m²+16m Δ=16 − 3m²+8m − 3m²+8m+16>0 Δ_m=64+3*16*4=256 //dobry znak Δ=16² m=−8−16/−6 v m=−8+16/−6

	4
m=4 v m==−
	3

F malejąca więc

	4
me ( −		; 4)
	3

liczymy dalej....

Marcin: Hugo. To takie zadanie na łatwe zdobycie punktów. Tyle ze trzeba uwazać, zeby się nie walnąć w obliczeniach

Hugo: z twarogu vieta x1+x2<2m2−3

	b
−		<2m2−3
	a

m−4
	<2m2−3
1

0<−m+4+2m²−3 2m²−m+1>0 Δ=1−.... Δ<0 me pustego :.............: serio?

Hugo: Obal mi to

Hugo: https://matematykaszkolna.pl/strona/2589.html jakie skurczybykstwo a już sie śmiałem że Vieta nie kazali przekształcać Oni sprowadzaja to to iloczynu (x+1)(....) <0 xe (−1; 00)

P@weł: mi tez wyszla Δ= −7 brak pierwiastkow

Marcin: m−4<2m²−3 2m²−m+1>0 Na pewno pustego?

Marcin: Hugo Twoim problemem jest to, ze źle czytasz treść zadania. Tam jest 2m³−3!

P@weł: Ale byka walneles przy przepisywania, no wiesz co ! od 2m³−3

Hugo: aaaaaaaaaa nie odzywam sie ta miało być wgl <2m³−3

P@weł: 2,5 pkt mniej D za zadanie

Hugo: To jest Marcinie wyzszy lvl robić zadanie bez czytania treści . . i tak sb dam fula

P@weł: ja bym sie nie pierdzielil w rozpisywanie tylko bym znalazl pierwiastek i schematem Hornera

Marcin: W Twoim przypadku i tak miałeś źle, bo wynikiem powinien być zbiór liczb rzeczywistych!

P@weł: " i tak sb dam fula " heheh

Hugo: czyli jak ni ma x₁ x₂ to jest xe R? .. ja tego nigdy nie wiem

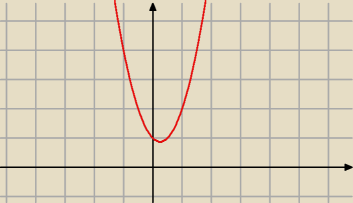
Marcin: Hugo! To powinieneś wiedzieć jak amen w paciezu! To jest wykres Twojej funkcji. Szukasz kiedy ona jest >0, bo taki masz warunek. Jak widać na powyzszym wykresie, jest ona zawsze nad osią OX, więc jest tez zawsze większa od 0, kpw?

P@weł: Gdy delta jest mniejsza od zera czyli : Δ<0 − oznacza ze brak miejsc zerowych https://matematykaszkolna.pl/strona/54.html Jak widzimy mamy funkcje kwadratową : 2m²−m+1 wspolczynnik "a" przed m² jest dodatni dlatego ramiona paraboli są do góry i nie dotykaja osi X bo brak miejsc zerowych , więc x∊R

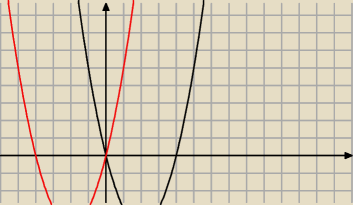
Hugo: Narysuj wykres funkcji f określonej wzorem f(x)=x²−4|x| i na jego podstawie wyznacz liczbe rozwiazan f(x)=m w zależności od wartości parametru m. f(x)=x²−4|x| to bym sb rozbił na x≥0 v x<0 1) x≥0 f(x)=x²−4x → x(x−4) 2) x<0 f(x)=x²+4x → x(x+4)

P@weł: Rozumiesz juz? jak nie to pytaj

Hugo: Marcin Marcin... w imię stoicyzmu poprzestaje na małym... Ale okej racje i ma to sens

Hugo: a całke byś mi wytłumaczył?

P@weł: PEWNIE!

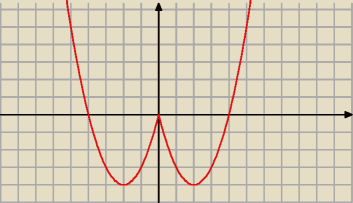
Marcin: No i świetnie. Teraz druga część zadania

P@weł: Żartowałem , nie pisz nie wysilaj sie D jeszcze na studiach nie bylem

Marcin: Całki i tak by Ci się raczej nie przydały w piątek

P@weł: Czarny piątek

Hugo: wiem wiem ale w wakacje cos bym ogarnął Co do wykresu to wiem ze tak ma być bo te przedziały mniejszy i większy od zera .. trza by wierzchołek q obliczyć

Δ
4a

Δ= f(x)=x²−4|x| //to wychodzi takie samo dla x>=0 v x<0 Δ=16

	16
q=		=4
	4

dla me (−oo, 4) − 0 rozw me (4≥ − 4 rozw me (0 ; oo) − 2 rozw zastanawiam sie jeszcze nad domknięciami <> ()

Marcin:

	Δ
q=−4, a nie 4 bo mamy wzór q=−
	4a

Hugo: me≤4 , 0≥ *

Hugo: racja ... nawet na wykresie widać.. dla me (−oo, 4) − 0 rozw me ≤−4 ; 0≥ − 4 rozw me (0 ; oo) − 2 rozw

Marcin: źle Hugo. Pomyśl

Hugo: aaaaaaaaaaaa −.− powinienem to na dwa przypadki z osobna ... : P

Marcin: dla m=−4 masz dwa rozwiązania. dla m=0 masz trzy rozwiązania.

Marcin: Nie. Na żadne dwa przypadki

Hugo: popatrzylem juz w odp no okej rozumiem

Hugo: https://matematykaszkolna.pl/strona/2590.html

Marcin: Cieszę się

P@weł: Nie dałbym rade chyba napisac matury w takim stanie w jakim teraz jestem tak patrzę na zadanie z tego linku https://matematykaszkolna.pl/forum/249082.html "4 maj 2014 02:48" i sie zastanawialem z 10 min jak on to zamienil .... chyba zmeczenie daje po sobie znac , trzeba bedzie dobrze sie wyspac przed matura

Hugo: tez bede mykać spac bo sie nie da Bywajcie i dz!

P@weł: Hugo Bywaj! Powodzenia ! <kop w D***> DD

Marcin: No jak to nie wiesz jak on to zmienił? Masz taki wzór log_ab + log_ac = log_abc. On to zastosował z drugą stronę

Marcin: Siemasz Hugo

P@weł: Marcin wiem wiem, tylko ze juz taki zmeczony jestem ze ledwo co do tego doszedlem ciezko ruszyc głowa przy zmeczeniu

P@weł: Marcin , uczysz sie cos jeszcze?

Marcin: Ja czytam na polski. Matmy nie ruszam. Tyle co pomagam na forum tylko

P@weł: ja to robie teraz jakies zadanka, jak cczegos nie bede wiedzial to bede pisal ,co?

Marcin: Ok, pewnie. Jak dam radę, to pomogę (nie pisz w sprawach prawdopodobieństwa )

P@weł: nie przerabiales jeszcze prawdopodobienstwa?

Marcin: Przerabiałem, ale jestem z niego bardzo słaby. Ogólnie to jestem samoukiem, bo nie miałem matmy rozszerzonej w szkole i nie chodziłem na korki. Dlatego mam duże braki

P@weł: rozumiem, ale te zadania z prawdopodobienstwa ktore byly na maturach raczej ogarniesz? np z obsadzaniem miejsc przez liczby

Marcin: Te co były ogarniam, bo juz je przerabiałem, a jak będzie na w piątek to nie mam pojęcia

P@weł: no fakt, wielka niewiadoma, chcialbym aby poziom byl jak zeszłorocznej

Marcin: Też bym się nie obraził, ale poziom na pewno wyzszy nie będzie

P@weł: ja nie umiem sie tak pocieszac jak ty

P@weł: Mam sin2x = 0 jak moge to skomentowac? to jest skracanie ? jak to bardziej sie fachowo nazywa

Marcin: A po co to komentować?

P@weł: a jakos tak zapytałem , ciekawiło mnie to

Marcin: Ja nie mam pojęcia jak to się 'fachowo' nazywa

P@weł: co do tego równania : sin2x = 0 2x = kπ <−−−−−−−−− Te "kπ" tyczy sie jeszcze do zwykłej funkcji sinx oznacza to ze miejsce zerowe występuje co π

	1
x=		kπ <−− 1/2kπ tyczy się juz do sin2x
	2

mam racje?

Marcin: Tak, masz rację.

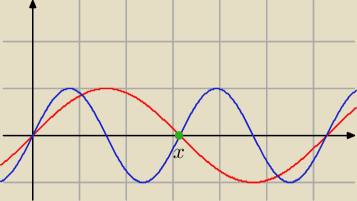
Marcin: x=π,

	1
teraz widać, ze w sin(2x), ten sam wynik masz co		π
	2

P@weł: Dzieki , chociaz i tak pewnie pozapominam

Marcin: W sytuacji, gdy sin(2x)=0 oczywiście

Marcin: Tu nie chodzi o naukę na pamięć. Tu chodzi o zrozumienie tego jak wygląda funkcja sin(x), czy sin(2x), później to idzie z automatu

P@weł:

	1
tzn jak skroci sie o połowę funkcje sinx to na oko widać ze miejscem zerowym bedzie		π
	2

Marcin: Ale na oko nic nie mozesz określać

muflon: P@weł pocieszam Cię, że w najgorszym wypadku nie poprawisz na gorzej