23 kwi 23:11
Marcin: Przecież masz tam wytłumaczone
23 kwi 23:23
bezendu:
Nie kumam właśnie
23 kwi 23:25
23 kwi 23:27
Mila:
Wyjaśniłam.
23 kwi 23:28
bezendu: Widziałem
23 kwi 23:31
Mila:
Zrozumiałeś?
23 kwi 23:32
bezendu:
Tak. Teraz zostało mi ostatnie zadania z Pazdro i mam zrobiony już cały ten zbiór.
Tylko to jedno którego nie umiem zrobić:
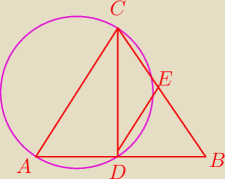
W trójkącie równoramiennym ABC, |AC|=|BC|, mamy dane |AB|=|CD|=8cm, gdzie CD jest wysokością
tego trójkąta. Zakreślono okrąg o średnicy AC. Punkty A. C oraz punkty przecięcia okręgu z
podstawa trójkąta i ramieniem BC wyznaczają czworokąt wpisany w okrąg
a. Wykonaj rysunek
b. Oblicz pole czworokąta wpisanego w okrąg
23 kwi 23:38
bezendu: ?
23 kwi 23:56
Marcin:
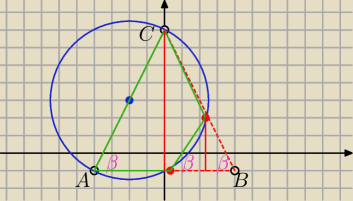
Pytanie do Mili:
Mogę sobie bez problemu 'wrzucać' zadania do układu współrzędnych i podstawiać normalnie
punkty, tak jak np tu?
B=(4;−1)
A=(−4;−1)
C=(0;7). czy nie bardzo?
Wybacz bezendu spam
23 kwi 23:57
Mila:
Rysunek dobry, okrąg przechodzi przez Punkt D, bo AC jest średnicą , a kąt ADC jest prosty,
więc jest wpisany w ten okrąg.
Możesz obliczyc pole ΔABC,
∡A=∡B=α ( Δrównoramienny⇒kąty przy podstawie równe)
∡A+∡E=180 Suma kątów przeciwległych w czworokącie wpisanym w okrąg
W takim razie:
∡E=180 − α ⇒∡DEB=α jako kąt przyległy
Masz ΔDBE o kątach α przy boku EB.⇔
ΔDBE∼ΔABC w skali , no właśnie znajdź, jeszcze chwilę będę, to sprawdzę, albo podpowiem.
24 kwi 00:04
Mila:
Marcin, masz dobrze.
24 kwi 00:05
Marcin: Ok, dziękuję
Ale czy mogę takim rysunkiem z tego cokolwiek liczyć?
Bo z rysunku od razu
widać, że np promień okręgu to będzie 2
√5. To można oczywiście wyliczyć podstawiając te
punkty, ale obawiam się że miałbym na to 0pkt
24 kwi 00:11
bezendu:
PΔABC=32
PADC=16
Czy trójkąt DBE jest równoboczny ?
24 kwi 00:12
Mila:
| | 8 | |
Nie może byc równoboczny bo tgα= |
| =2, |
| | 4 | |
Jest równoramienny i to Ci wystarczy. Jest podobny do ΔABC.
Zlokalizuj ramiona i podstawę
| | AC | |
Skala podobieństwa k= |
| (ramię do ramienia) |
| | DB | |
P
ΔDBE=k
2*32
24 kwi 00:18
bezendu:
DBE jest równoramienny ?
24 kwi 00:19
Mila:
Dobranoc, walczcie razem z Marcinem.
24 kwi 00:19
bezendu:
Dobranoc... Powalczę sam jeszcze ponad 100 zadań....ehh
24 kwi 00:20
Marcin: Dobrej nocy Milu
24 kwi 00:21
Marcin: beznedu. skoro ABC ≈ DBE, to musi być równoramienny
24 kwi 00:21
bezendu:
Ja jakoś tego nie widzę.. Powtarzam, że nie umiem planimetrii a uczyłem się jej całe wakacje
24 kwi 00:23
Marcin: No ale przecież ich podobieństwo oznacza, że mają takie same kąty. Więc tak musi być
24 kwi 00:25
Eta:
24 kwi 00:28
bezendu:
Eta 
bo
24 kwi 00:29
24 kwi 00:31
bezendu:
Po maturze jak będzie dobrze napisana to się skuszę na jedno...
24 kwi 00:32
Eta:
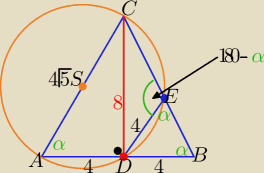
ΔABC ~ ΔDBE z cechy (kkk)
| | 4 | | 1 | | 1 | |
k= |
| = |
| , k2= |
| |
| | 4√5 | | √5 | | 5 | |
| | 32 | |
P(ADEC)= 32− |
| = ...... |
| | 5 | |
i po b
ólu
24 kwi 00:41
bezendu:
Skąd wiesz, że odcinek DE=4 ?
24 kwi 00:43
Eta:
Nie osłabiaj mnie
Skoro ma równe miary kątów przy podstawie.... to jest równoramienny o ramionach dł. 4
24 kwi 00:45
bezendu:
Kat <B i kąt ∡A są takie same jak dla mnie.
''Nie osłabiaj mnie'' za późno
24 kwi 00:47
Eta:
Chodzi o trójkąt DBE..... ,że też jest równoramienny
24 kwi 00:52
bezendu:
ok to już wywnioskowałem
24 kwi 00:53
Eta:
No i
więcej poprawnych wniosków
24 kwi 00:54
bezendu:
za wolno to wszystko do mnie dociera
24 kwi 00:56
Eta:
Wierzę w Ciebie
zdasz maturę na 100%
24 kwi 00:57
bezendu:
Bardzo bym chciał
24 kwi 00:57
Eta:
W tym roku będzie łatwa
24 kwi 00:58
bezendu:
Wszystkie matury od 2010 do 2013 robiąc zrobiłem bezbłędnie nawet planimetrię.
Może być trudna tylko żeby dowodzik był prosty
24 kwi 01:00
bezendu:
jesteś jeszcze ?
24 kwi 01:02
bezendu: W trójkąt równoramienny ABC , w którym |AC | = |BC | , |∡ACB | = 1200 , wpisano okrąg,
którego promień ma długość r . Oblicz długości boków trójkąta
24 kwi 01:06
bezendu: ?
24 kwi 01:26
Hugo: bezbłędnie i nie napiszesz matury na 100
? czarowałeś mnie na GG
24 kwi 01:27
Eta:
| | 4 | |
|AB|=2r(2+√3) , |AC|=|BC|=r(2+ |
| √3) |
| | 3 | |
Licz... (leniu)
24 kwi 01:27
bezendu:
Hugo co Ty bierzesz ?
24 kwi 01:31
bezendu:
Eta wytłumacz na dobranoc, proszę ?
24 kwi 01:33
bezendu:
oprócz rysunku to nic tu nie mam
24 kwi 01:39
zombi:
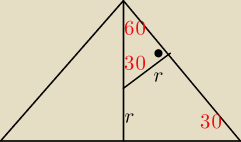
Wystarczy?
24 kwi 01:46
Eta:
Z trójkątów "ekierek" 30,60,90
| | 2r√3 | | r | |
|OC|= |
| ( lub z f. tryg. |
| =sin60o ⇒ |
| | 3 | | |OC| | |
|CD|=r+|OC|= ......
|BC|= 2*|CD| =........
|DB|=|CD|*
√3=.......
24 kwi 01:51
bezendu:
Dziękuję.
24 kwi 10:31
bezendu:
Dany jest trójkąt równoramienny ABC , w którym |AC | = |BC | = b i |AB | = a . Punkty M i N
są rzutami środka podstawy AB trójkąta na ramiona BC i AC . Wyraź pole czworokąta ABMN za
pomocą a i b .
24 kwi 13:43
bezendu: ?
24 kwi 18:24
Mila:
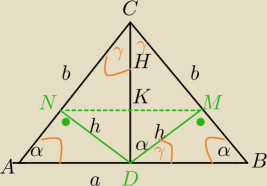
Masz zaznaczone kąty, nie lubisz podobieństwa, to może licz z proporcji trygonometrycznych.
24 kwi 18:42
bezendu: Dobrze.
24 kwi 19:02
Mila:
To są dość koszmarne obliczenia.
24 kwi 19:03
Mila:
Może lepiej zając się bardziej prawdopodobnym zadaniem z geometrii?
No, ćwicz dalej charakter.
24 kwi 19:10
bezendu:
Bardziej prawdopodobnymi tzn jakimi ?
Trapezy ?
24 kwi 19:11
Piotr 10: Chcesz trapezik to masz
Dlugosci ramion trapezu opisanego na okregu sa rowne c=4 , d=8. Środkowa trapezu dzieli go na
dwa trapezy z ktorych mniejszy ma pole trzy razy mniejsze od pola danego trapezu. Wyznacz
dlugosci podstaw danego trapezu.
24 kwi 19:27
Mila:
To ,jak piszemy rozw. zadania z 13:43 w ramach ćwiczenia biegłości w rachunkach?
24 kwi 20:15
bezendu:
Odpuszczam tę zadania, skoro one nie są maturalne. W wakacje sobie wrócę do tego..
24 kwi 20:18
Mila:
To jakie zadania teraz robisz?
24 kwi 20:21
bezendu:
Arkusze kończę, a im bliżej tym mniej motywacji..
24 kwi 20:22
Mila:
Może więcej nerwów ?, to normalne.
Pisz problemy.
24 kwi 20:53
bezendu:
Ja się nie denerwuję
No może troszkę ale to tylko ze względu na planimetrię
24 kwi 20:54
bezendu: Nadal nie rozumiem tych średnich.
24 kwi 21:10
Mila:
To pisz zadanko.
24 kwi 21:14
bezendu:
To już pisałem, chodzi o ten romb co kiedyś wstawiałem.
24 kwi 21:15
Mila:
Zadanie z rombem zalicza się do trudnych, Ty niektórych zależności nie widzisz na rysunku, może
popracuj nad tym, aby wyciagac wnioski z danych, wróć do problemów .
Niekoniecznie do wszystkich naraz.
24 kwi 21:22
bezendu:
Zadanie z rombem pochodzi ze zbioru Pazdro..
24 kwi 21:23
Mila:
Wiem, w podręczniku III klasa− Kurczb, Świda ( z oficyny Pazdro) jest wyprowadzony wzór. Nie
powiem Ci jakim sposobem, bo przelotnie spojrzałam już dość dawno.
24 kwi 21:35
bezendu:
Akurat w swojej edukacji nie korzystałem z tego podręcznika
24 kwi 21:40
bezendu: Kąty ostre trójkąta ABC o polu S mają miary |∡A | = α , |∡B | = β . Oblicz długości boków AB
i BC tego trójkąta.
24 kwi 21:45
kyrtap : z układu pojedź
24 kwi 21:50
Mila:
Podpowiedź.
1)Tw. sinusów
24 kwi 21:54
bezendu:
| | a | |
U{b}[sinB}= |
| co mi to daje ? |
| | sinα | |
24 kwi 21:55
Mila:
Masz obliczyć a i c, to skorzystaj z tego związku:
Oblicz c i podstaw do wzoru
24 kwi 22:05
bezendu:
csinα=asin(α+β)
Teraz już chyba powinno wyjść
24 kwi 22:09
bezendu:
Dziękuję, wyszło poprawnie ale po jakich męczarniach...
24 kwi 22:14
Mila:
Nie przesadzaj.
24 kwi 22:18
bezendu:
Nie przesadzam.
24 kwi 22:21
24 kwi 22:25
24 kwi 22:28
Mila:
3) Albo tak:
α+β+γ=180 w ΔABC
α+β<180 /:2
| 1 | | 1 | |
| α+ |
| β<90 ⇒90o<∡APB<180o |
| 2 | | 2 | |
24 kwi 22:35
Mila:
4)
Na okręgu o promieniu 2cm opisano trójkąt prostokątny, którego przeciwprostokątna ma długość
10cm. Oblicz pole i obwód tego trójkąta.
24 kwi 22:36
bezendu:
w trójkącie ABC mamy dane: |AC| = √3 i kąt ACB to 900. Przez wierzchołek C poprowadzono
prostą, która utworzyła z bokiem AC kąt 600 i przecięła bok AB w punkcie D tak, że |AD| :
|DB| = 1:3. Oblicz długość boków AB i BC oraz odcinka CD.
24 kwi 22:37
24 kwi 22:37
bezendu:
4) widziałem na forum, robiłem na kartce ale nie pisałem bo za dużo wpisywanie było
boki 6 i 8
24 kwi 22:39
zawodus: dwa wzory
24 kwi 22:39
bezendu:
w którym ?
24 kwi 22:41
Mila:
Dziękuję Eta.
Masz zrobić tak, aby było mało pisania. Pomyśl.
I nie liczyć długości boków!
Pamiętaj , że punkty styczności okręgu są jednakowo odległe od wierzchołków kata.
24 kwi 22:43
zawodus: już zrobione więc w żadnym
24 kwi 22:43
Eta:
24 kwi 22:44
bezendu:
Ja się cieszę, że wgl zrobiłem już nie chodzi o sposób
24 kwi 22:44
Eta:
24 kwi 22:45
Mila:
No, to wcale mi się nie podoba, że w Twoim sposobie jest dużo obliczeń.
No to zobacz jak tam Eta rozwiązała, chwilę zadumy Ci zalecam. (Czas to pieniądz podobno)
24 kwi 22:49
bezendu:
Planimetrię zostawiam na koniec.
Dojść jakoś do celu potrafi wielu,ale najkrótszą drogą nieliczni mogą.
24 kwi 22:56
bezendu:
A wracając do zadania 22:37 ?
24 kwi 22:58
Mila:
P ΔCDB=3*PΔADC ( maja wspólną wysokość a stosunek podstaw 3), stąd obliczysz a
24 kwi 23:17
bezendu:
spróbuje
24 kwi 23:18
Mila:
Jak?
24 kwi 23:37
Mila:
Narysuj rysunek z oznaczeniami.
24 kwi 23:38
bezendu:
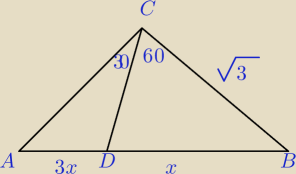
Tyle umiem..
24 kwi 23:43
Mila:
No nie jest zgodne z treścią. Sprawdź, czy dobrze przepisałeś treść zadania, bo mi się nic nie
zgadza.
AD: DB=1: 3. no to nie jest tak na rysunku.
25 kwi 00:02
bezendu:
w trójkącie ABC mamy dane: |AC| = √3 i kąt ACB to 900. Przez wierzchołek C poprowadzono
prostą, która utworzyła z bokiem AC kąt 600 i przecięła bok AB w punkcie D tak, że |AD| :
|DB| = 1:3. Oblicz długość boków AB i BC oraz odcinka CD.
25 kwi 00:04
bezendu:
dobranoc
25 kwi 00:13
zawodus: Bezendu twój rysunek jest całkowicie inny
Jakbyś go w lusterku odbił
25 kwi 07:35
Piotr 10: Czy tresc jest dobra ? Bo u mnie z rysunku wynika, ze IADI > IDBI , a to chyba falsz jakis. Bo
przeciez
IDBI=3*IADI
A tutaj , ze IDBI > IADI
25 kwi 09:16
Mila:
Właśnie mam Piotrze podejrzenie, że błąd w treści.
25 kwi 18:01
25 kwi 18:02
Mila:
Może powinno być?
"Przez wierzchołek C poprowadzono
prostą, która utworzyła z bokiem AC kąt 30o "
Albo
"Przez wierzchołek C poprowadzono
prostą, która utworzyła z bokiem BC kąt 60o "
25 kwi 18:24
zawodus: No i co dobra treść czy nie?
25 kwi 18:26
bezendu:
Szukałem i w innym arkuszu jest przez wierzchołek C, ale w arkuszu jest tak jak podałem..
25 kwi 18:26
Mila:
Skąd masz ten arkusz?
25 kwi 18:32
bezendu:
Znaleziony kiedyś na internecie.
25 kwi 18:37
Mila:
A jaka tam jest odpowiedź?
To może rozwiąż takie zadanie:
W trójkącie ABC mamy dane: |AC| = √3 i kąt ACB to 900. Przez wierzchołek C poprowadzono
prostą, która utworzyła z bokiem AC kąt 30o i przecięła bok AB w punkcie D tak,
że |AD| : |DB| = 1:3. Oblicz długość boków AB i BC oraz odcinka CD.
25 kwi 18:45
bezendu:
Nie ma odpowiedzi.
25 kwi 18:45
Mila:
To rozwiąż moją wersję.
25 kwi 18:52
bezendu:
Do tego zadania mój rysunek jest odpowiedni ?
25 kwi 19:00
Mila: boki źle opisane, kąty dobrze.
25 kwi 19:10
bezendu:
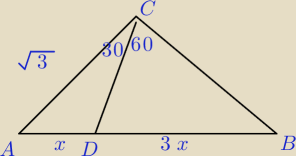
25 kwi 19:16
Mila:
ΔADC i ΔCDB mają wspólna wysokość (opuszczoną na AB) i |DB|=3*|AD|⇔
3*P
ΔADC=P
ΔCDB
|CD|=d, |CB|=a
| | 1 | | 1 | |
3* |
| *√3*d*sin30o= |
| *d*a*sin60o |
| | 2 | | 2 | |
Działaj dalej sam.
25 kwi 20:18
bezendu:
Tylko żebym jeszcze wiedział skąd się to wzięło
25 kwi 20:26
25 kwi 20:30
bezendu:
Dziękuję, ale to chyba za trudne dla mnie.
25 kwi 20:38
Mila:
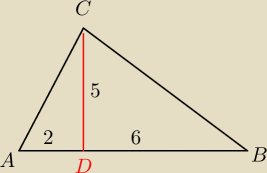
No nie żartuj. Przecież umiesz obliczać pole trójkąta na różne sposoby.
AD=2
DB=6
Ile razy pole ΔCDB jest większe od pola ΔADC?
25 kwi 20:59
bezendu:
Umiem i co z tego wynika ? A do żartów do nawet nastroju nie mam.
25 kwi 21:00
Mila:
ΔADC ma pole 3 razy mniejsze od pola ΔCDB
.
Tak samo jest w Twoim zadaniu.
Liczymy pola tych Δ ze wzoru :
| | 1 | | 1 | | 1 | | √3*CD | |
PΔADC= |
| *AC*CD*sin30o= |
| *√3*CD* |
| = |
| |
| | 2 | | 2 | | 2 | | 4 | |
| | 1 | | 1 | | √3 | | CD*CB*√3 | |
P ΔCDB= |
| *CD*CB*sin60o= |
| *CD*CB* |
| = |
| |
| | 2 | | 2 | | 2 | | 4 | |
|CB|=3
Dalej
|AB|
2=(
√3)
2+3
2
25 kwi 21:18
bezendu:
|AB|=12
25 kwi 21:34
Mila:
|AB|=√12=2√3
25 kwi 21:59
bezendu: fakt.
25 kwi 22:00
bezendu: ?
Może skończmy to zadanie, bo nie chcę się już kompromitować
25 kwi 22:28
Mila:
A masz problem ze skończeniem?
Oblicz x,
25 kwi 23:04
bezendu:
Moim problem jest słowo−Planimetria.
Już dokończyłem, dziękuję.
25 kwi 23:13
Mila:
25 kwi 23:13
bezendu:
Już nie będę robił tych zadań, bo się tylko stresuję i spać potem przez to nie mogę.
25 kwi 23:16
5-latek: bezendu
spojrz tu i napisz albo tak jak napisales ostatnio albo jak chcesz to podam Ci emalia
25 kwi 23:18
25 kwi 23:18
bezendu:
Napisałem i czekam na odpowiedź.
25 kwi 23:19
bezendu:
A tak wracając do zadania, trzeba koniecznie z podobieństwa ?
25 kwi 23:22
Mila:
W jakim zadaniu to podobieństwo?
25 kwi 23:25
bezendu:
W tym co wstawiłem podobieństwo trójkątów
25 kwi 23:25
5-latek: Zaraz spojrze na poczte .
25 kwi 23:26
Mila:
Bezendu z której godziny wpis?
25 kwi 23:51
bezendu:
20:30
26 kwi 00:00
Mila:
Tam nie ma podobieństwa, tylko badałam iloraz pól.
26 kwi 00:03
bezendu:
To już wgl nie rozumiem.
26 kwi 00:04
Mila:
Dobranoc.
26 kwi 00:07
bezendu:
Zadanie zrobione, bez żadnych skali i porównywania. Twierdzenie sinusów+twierdzenie cosinusów
27 kwi 18:34
Mila:
I bardzo dobrze.
27 kwi 18:36
bezendu:
Trochę to zajęło, ale zrobione.
27 kwi 18:43
