matura rozszerzona Hiromi_Ise: w trójkącie ABC mamy dane: |AC| = √3 i kąt ACB to 90⁰. Przez wierzchołek C poprowadzono prostą, która utworzyła z bokiem AC kąt 60⁰ i przecięła bok AB w punkcie D tak, że |AD| : |DB| = 1:3. Oblicz długość boków AB i BC oraz odcinka CD.

rumpek:

	|AD|		1
1o		=
	|DB|		3

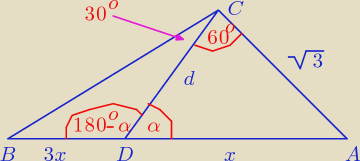
3|AD| = |DB| 2^o Tw. Pitagorasa (√3)² + b² = (4x²)² 3 + b² = 16x² b² = 16x² − 3, b∊R₊ b = √16x² − 3, 16x² − 3 ≥ 0 3^o Tw. sinusów: [trójkąt ADC]

√3		x
	=
sinα		sin60o

	√3
√3 *		= sinαx
	2

3
	= sinαx / : x
2

	3
sinα =
	2x

4^o Tw. sinusów [trójkąt DBC]

3x		b
	=
sin30o		sin(180o − α)

	1
3x * sinα =		* b [zastosowałem wzór redukcyjny (sin(180o − α) = sinα]
	2

b = 9 √16x² − 3 = 9 / ()² 16x² − 3 = 81 16x² = 84 / : 4

	21
x2 =		, x∊R+
	4

	√21
x =
	2

5^o Podstawiam pod b = √16x² − 3 ⇒ b = √4 * 21 − 3 ⇒ b = √84 − 3 ⇒ b = 9. Zatem

	√21
|AB| = 4 *		= 2√21
	2

6^o. Tw. cosinusów [trójkąt ACD] x² = √3² + d² − 2√3d*cos60^o

21
	= 3 + d2 − √3d / * 4
4

21 = 12 + 4d² − 4√3d 4d² − 4√3d − 9 = 0 Δ_d = 48 + 144 = 192 ⇒ √Δ = 8√3

	4√3
d1 = −		∉ R+
	8

	3√3
d2 =
	2

gfgs: dlaczego naprzeciwko większego konta jest mniejszy bok

Lk: Z jakiego zbioru zadan jest to zadanie ?

janek191: Zadanie z 1 maja 2012 r. Rysunek nie oddaje rzeczywistych proporcji w tym trójkącie.

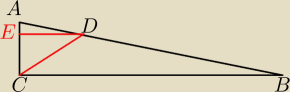
an: Można to trochę uprościć

	3√3
EC=
	4

ECD trójkąt prostokątny ∡ECD=60^o

	3√3
CD=2EC=
	2

Z tw cosinusów

	27		3√3		21
|AD|2=		+3 −2		*√3*cos60o=
	4		2		4

AB=4AD=2√21 z Pitagorasa BC=√84−3=9

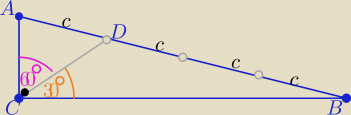
b4: Zadanie o takiej treści ( błędnej) nie ma rozwiązania Taki trójkąt nie istnieje

an: a to niby czemu

b4: A no temu,że naprzeciw większego kąta leży krótszy bok ?

an: Przecież tam są dwa trójkąty i wszystko z kątami jest OK. Co do tego jakie tam są konta jak pisze @gfgs głosu nie zabieram bo nie wiem gdzie te konta są.

ABC: najlepsze jest konto z dużym debetem

b4: Naprzecie 60^o bok c naprzeciw 30^o bok 3c Czy to jest poprawne?

b4: Naprzeciw 60^o

a7: 23:44 nie zgodzę się, gdyż najlepsze są chyba jednak te z dużym saldem końcowym(?)

a7: (do tego dodatnim oczywiście)

an: W trójkącie ACD jest kąt 60^o, a w trójkącie CDB kąt 30^o i odpowiednio boki c i 3c, a tak na przyszłość sam narysowałeś te trójkąty zgodnie z zadaniem mniej więcej w skali i nie wierzysz , że istnieje.

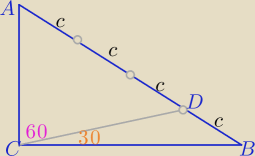
b4: W treści powinno być : |AD| : |DB|=3:1 ( a nie 1:3

an: Oczywiście mogłoby by być jak napisałeś o 00:08, ale rozwiązanie zgodnie z treścią początkową istnieje i jest prawidłowe.

b4: Dane w treści są sprzeczne

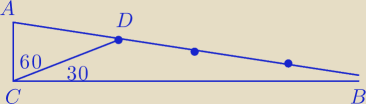
a7: @b4 an ma rację, wystarczy aby AC było odpowiednio/proporcjonalnie niskie , a BC odpowiednio długie

a7: ja rozumiem rozwiązanie an, jakby co, mogę wytłumaczyć

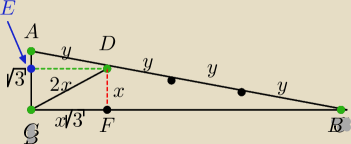
a7: z podobieństwa trójkątów ABC i DFB (k,k,k)

4y		3y
	=
√3		x

	3√3
x=
	4

	3√3
czyli 2x=|CD|=
	2

==================== |CF|=x√3=9/4

	3√3		√3
AE=AC−x=√3−		=
	4		4

z podobieństwa trójkątów ABC i ADE (k,k,k)

|AC|		|AE|
	=		ED=CF
|CB|		|ED|

	√3
czyli U{√3}{|CB|=		:(9/4)
	4

czyli |BC|=9 =============== z tw. Pitagorasa |AB|=√81+3=√84=2√21 ======================