mix Rafal: Od ostatnich łańcuszków maturalnych minęło już trochę czasu, więc pomyślałem o wznowieniu. Zasady proste: osoba, która wrzuca rozwiązanie, wrzuca swoje zadanie lub oddaje. Coś na początek: (1) Proszę uzasadnić, że dla dowolnej liczby całkowitej k liczba 2k³−3k²−8k−3 dzieli się przez 3.

StrasznyNieogar: 2k²(k +1) − 5k(k+1) − 3(k+1) = (k+1)(k+2)(k−6)

Rafal: Coś nie poszło Gdzie ta 2 z przodu?

relaa: Chyba coś nie za bardzo.

StrasznyNieogar: wiem, nie tędy droga przez przypadek wysłałem

relaa: Może coś takiego. 2k³ − 3k² − 8k − 3 = 2(k − 1)k(k + 1) − 3(k + 1)²

Rafal: relaa, skoro już jesteś, zerkniesz może tu https://matematykaszkolna.pl/forum/352790.html ?

relaa: Jakiegoś super prostego sposobu nie widziałem na obliczenie tej reszty. Możesz popróbować swoimi sposobami i zobaczyć co Ci tam wyjdzie.

astro: 2k³−3k²−8k−3=(2k+1)(k+1)(k−3) 1) Jeżeli k podzielne przez 3, czyli k=3l to wyrażenie (k−3) jest podzielne przez 3 2) Jeżeli k przy dzieleniu przez 3 daje reszte 1, to k=3l+1 i wtedy 2k+1=2(3l+1)+1=6l+3 podzielne przez 3 3) Jeżeli k przy dzieleniu przez 3 daje reszte 2, to k=3l+2 i wtedy k+1=3l+3 jest podzielne przez 3

Rafal: astro, masz kolejne zadanie?

Rafal: relaa, OK

astro:

	1		1
Udowodnij, że dla każdego n ∊ N zachodzi		≤ n√2−1 ≤
	2n		n

Rafal: Szkoda, że nie ma tu Adamma Może czas w końcu zdjąć tego bana, w końcu poszło o głupotę, a minął już tydzień.

relaa: Wyrażenie 2(k − 1)k(k + 1) dzieli się przez 3 jako iloczyn trzech kolejnych liczb oraz 3(k + 1)² jako wielokrotność 3, zatem różnica 2(k − 1)k(k + 1) i 3(k + 1)² dzieli się przez 3.

Adam: Rafal, spokojnie, zabezpieczenia tego forum się mnie nie imają

Rafal: Adam

Eta:

Kacper: Czyli masz szczęście

Rafal: astroo, w tym zadaniu chodzi o to, by uzasadnić monotoniczność odpowiednich ciągów, policzyć granice itd., czy jest może jakieś ładne rozwiązanie korzystające z klasycznych nierówności?

Eta: Jakie .... ostatnio forum ..... to i takie i zabezpieczenia

astro: Taak, bardzo podstawowo to sie da zrobić

astro:

	1		1
n√2−1≤		czyli 2≤(1+		)n
	n		n

to łatwiejsze

Rafal: Aaa... byłem ślepy i przejrzałem. Za chwilę coś wrzucę.

Rafal: Nie wiem w jakim kierunku powinien ten mix, ale skoro już zaczęliśmy z takimi niestandardowymi jak na maturę zadankami, to... prosto z finału tegorocznego konkursu X: Dana jest taka liczba naturalna n>1, dla której liczba 2²ⁿ⁻¹−1 jest liczbą pierwszą. Wykaż, że również liczba n jest liczbą pierwszą.

Rafal: Wskazówka: warto rozważyć dowód nie wprost i skorzystać ze wzoru k^l−1=...

Rafal: OK, trochę słabo idzie, więc proszę kogoś życzliwego, by wrzucił jakieś fajniejsze zadanie. Rozwiązanie powyższego można znaleźć tu: http://skm.katowice.pl/zadania

Krzysiek: Rozwiaz równanie xy(x + 2017y) = 2017²⁰¹⁶ w zbiorze liczb calkowitych.

Adam: 2017 jest liczbą pierwszą x=2017ⁿ y=2017^m, m i n to liczby naturalne dodatnie 2017^n+m(2017ⁿ+2017^m+1)=2017²⁰¹⁶ jeśli n<m+1 1+2017^m+1−n=2017^{2016−2n−m} teraz musi być 2017|1+2017^m+1−n, skąd 2017|1 sprzeczność jeśli n=m+1 to możemy sprawdzić że 2=2017^{2016−2n−m}, musi być 2017|2 lub 1=2, sprzeczność jedyna opcja to n>m+1, wtedy 2017^n−m−1+1=2017^{2016−n−2m−1} i tymi samymi rozważaniami dochodzimy do sprzeczności ok?

Adam: moje zadanie: niech x₁, x₂, x₃ oznaczają pierwiastki wielomianu x³−3x+1

	x1		x2		x3
oblicz		+		+
	x1−1		x2−1		x3−1

zadanie stosunkowo łatwe

Jerzy: To ja odświeżę zadanie sprzed kilku dni ..... Dla jakiego m dziedziną funkcji jest zbiór jednoelementowy. f(x) = √1 − x + √−x² + 2mx − 4

Adam: Jerzy

Jerzy: Czyżbyś rozpoznał ?

Rafal: Adam, czyżby chodziło o wymnożenie i skorzystanie ze wzorów niejakiego Francois Viete'a, czy znowu czegoś nie widzę?

Adam: Rafal, jak najbardziej

Adam: ale możliwe że nie widzisz jeszcze wszystkiego

Rafal: Chwila, znajdę coś

Rafal: O, nie dziwi mnie to Jest jakiś sprytny sposób?

Adam: nie wiem co do licznika, ale co do mianownika to przecież jest wartość funkcji dla x=1 pomnożona przez −1

Adam: o, a nawet inną wersję podałem, to dokładnie wartość dla x=1

Rafal: O, faktycznie!

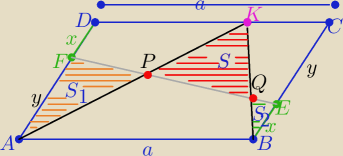
Rafal: Nie wiem, czy łatwe, czy trudne, ale wygląda fajnie. Punkty E i F leżą na bokach BC i DA równoległoboku ABCD, przy czym BE = DF. Punkt K leży na boku CD. Prosta EF przecina odcinki AK i BK odpowiednio w punktach P i Q. Wykazać, że suma pól trójkątów AP F i BQE jest równa polu trójkąta KP Q.

Krzysiek: moje zadanie można duużo prościej zrobić

Adam: x|2017²⁰¹⁶ oraz y|2017²⁰¹⁶ oraz x+2017y|2017²⁰¹⁶ skąd wynika że 2016y|2017²⁰¹⁶ co prawdą być nie może ok?

oleander: 1 − x ≥ 0 I −x² + 2mx − 4 ≥0 x ≤ 1 x² − 2mx + 4 ≤0 i żeby z tych warunków było 1 rozwiazanie m∊ {−1}

Jerzy: Dla m = −1 dziedzina jest zbiorem pustym.

oleander: przecież −2 należy wtedy do dziedziny? chyba że czegoś tu nie ogarniam

Jerzy: Dla: m = −1 −x² −2x − 4 < 0 dla dowolnego x

oleander: Dla: m = −1 −x2 −2x − 4 ≤ 0 dla dowolnego x

oleander: Dla: m = −1 −x2 −2x − 4 ≤ 0 dla dowolnego x

Jerzy: Jest zawsze ujemne , a więc nie istnieje drugi pierwiastek.

WITT: To moze takie zadanie :

	1		1
Dla kata ostrego α zachodzi zaleznosc :		+		= 4
	(sinα)2		(cosα)2

Obliczyc wartosc wyrazenia : w = sin³ α + cos³ α

oleander: może być też równy zero Δ= 4−4 =0

Jerzy: Δ = (−2)² − 4*(−1)*(−4) = 4 − 16 = −12

Eta: w=√2/2

Krzysiek: Adam, nadal można prościej

Adam: cóż, teraz już jest bardzo prosto, więc więcej mi nie trzeba

Krzysiek: Rozwiaz równanie x(x + 1) + (x + 1)(x + 2) + (x + 2)(x + 3) + . . . + (x + 14)(x + 15) = 2016x + 2017 w zbiorze liczb calkowitych.

Adam: lewa strona musi być nieparzysta ale ponieważ składa się z sumy iloczynów 2 kolejnych liczb to jest parzysta zatem rozwiązań nie ma

astro:

Krzysiek: brawo

Adam: Pokazać że jeśli okrąg przecina krzywą y=x³−25x w sześciu miejscach (x_i; y_i), 1≤i≤6 to suma x₁+x₂+...+x₆ nie zależy od położenia środku tego okręgu ani od jego promienia

Adam: zadanie stosunkowo proste, patrząc skąd je wziąłem

kubuk: w sześciu?

Adam: tak

kubuk: narysuj

Eta: Zadanie od Rafała wpis : 20:08 Zgodnie z treścią zadania: trapezy ABEF i CDCEF mają równe pola : oznaczam je przez P to: P−S=P−(S₁+S₂) ⇒ S=S₁+S₂ ========== c.n.w

Adam: kubuk, tutaj wykres się nie mieści Eta, coś więcej na temat równości P−S=... ?

Eta: A co chcesz więcej?

kubuk: całusa

Adam: no nie wiem, skąd się wzięła tak po prostu przecież nie powstała, a z rysunku nie mogę tego wywnioskować

Eta: Na "całusa" trzeba zasłużyć A ... .... może być?

kubuk: no na początek , całus będzie na randce!

Adam: to zadania 22:57, wiedza licealna zupełnie wystarcza

Adam: do*

Eta: Gdzie "zjadłeś" drugie "m" ? (Adamm

Adam: Eta, nick nie był po to by mnie rozpoznawano, tylko po to by ludzie mówili mi po imieniu gdyby Adam nie był zajęty, to bym go używał

kubuk: a co ty anETA tak nie śpisz jeszcze?!

Mila: Zadanie do łańcuszka. Oblicz piąty wyraz ciągu arytmetycznego: log₂(x₁), log₂(x₂), log₂(x₃),... wiedząc, że:

	7		1
x1+x2+x3=		oraz x3=
	8		2

kubuk: a MIla to od Kamila, tak?

Eta: {a_n} : −3,−2,−1,0,1 a₅=1

Kaacper:

	log2x1+log2x2
log2x2=		=> 2log2x2=log2x1x3 => 2x2=x1*12 => 4x2=x1
	2

	3
x1+x2=
	8

	3
4x2+x2=
	8

	3
x2=
	40

	3		12		3
x1=		−x2=		=
	8		40		10

	3
Coś źle, x1, x2 niepoprawne mi wyszły, log2		= / = −2
	40

Eta: x₁,x₂,x₃>0 2log₂x₂=log₂x₁+log₂x₃ ⇒ x₂²=x₁*x₃ i licz dalej...........

Kaacper: x₂²=x₁*¹₂ x₁=2x₂² 2x₂²+x₂=³₈ 2x₂²+x₂−³₈=0 Δ=4

	3
x2'= −		odrzucam
	4

	1
x2''=
	4

	1
x1=
	8

	1		1
log2		=log2		+(2−1)r
	4		8

r=1 a₁=−3, a₂=−2 więc a₅=1

www: Wykres funkcji y=2x³−x²−7x+6 oraz y=x+2 ma trzy punkty wspólne A,B,C. Jak jest maksymalna wartość sumy AB+AC?

Geniusz: x=2, −2, 0.5 to są te miejsca wspólne

Rafal: Może dla porządku: Eta miała na prawdopodobnie na myśli, że pole trójkąta ABK jest równe polu trapeza ABEF − stąd ta równość. Adam, dasz może jakąś wkazówkę? Mi zaraz głowa wybuchnie, a nikt inny też się nie kwapi, by je rozwiązać, pewnie ma być, że ∑_i=1ⁿx_i=0, ale jak?

marta: Dany jest czworokąt wypukły ABCD oraz AB=8,AD=5 zachodzą też równości ∡ABD=∡BCD, ∡ADB=∡ABD+∡BDC . Oblicz długość BC.

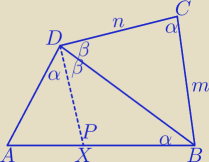
Rafal: Czyżby chodziło o podobieństwo: ΔXBD∼ΔBCD ΔAXD∼ΔADB ?

marta: czyli ile wynosi BC?

Rafal: AX=x BX=8−x DX=d BD=c Z podobieństwa ΔAXD∼ΔADB:

5		x		25		39
	=		⇒ x=		⇒ 8−x=
8		5		8		8

Z tego samego podobieństwa:

5		d
	=
8		c

Z podobieństwa ΔXBD∼ΔBCD:

x−8		d
	=
m		c

39   8		5
	=
m		8

39		5
	=
8m		8

39=5m m=7,8 OK?

marta: dobrze

Rafal: Za chwilę coś wrzucę.

Rafal: Wyznacz wszystkie funkcje f:R→R, które dla dowolnych liczb rzeczywistych x i y spełniają równanie f(x)·f(y) = f(xy)+x²+y².

liniowo niezależny: https://matematykaszkolna.pl/forum/353204.html

Kacper: Rafał f(x)=x²+1

Rafal: Tak, Kacper Właśnie roztrzaskałeś finał Śląskiego Konkursu Matematycznego sprzed kilku lat Wrzucisz coś?

Kacper: Cieszę się, że coś tam potrafię Chyba proste

	2π		4π		6π		1
Uzasadnij, że cos		+cos		+cos		=−
	7		7		7		2

marta: Rozwiązanie zadania Adama : Przekształcając równanie okregu (x−a)²+(x³−25x−b)²=r² x⁶ = −a² + x (2 a − 50 b) − b² + 2 b x³ + r² + 50 x⁴ − 626 x² zatem przy x⁶ mamy 1 a przy x⁵ mamy 0 więc z wzorów Vieta ta suma wynosi 0.

marta: Oblicz sumę bez kalkulatora

	1		1		1		1
		+		+		+
	sin26o		sin242o		sin266o		sin278o

www: z cosinusami https://zadane.pl/zadanie/9776009

Rafal: Kacper, jednak nie proste, ale za to bardzo rozwijające

liniowo niezależny: nikt nie zna się na algebrze liniowej

Adam: f(x)*f(y)=f(xy)+x²+y² f(x)*f(1)=f(x)+x²+1 f(x)*(f(1)−1)=x²+1 f(1)≠1 ponieważ prawa strona jest dodatnia

	x2+1
f(x)=
	f(1)−1

f(1)²−f(1)−2=0 f(1)=−1 lub f(1)=2 f(x)=x²+1 lub f(x)=−x²/2−1/2 podstawiając sprawdzamy że tylko f(x)=x²+1 spełnia nasze równanie dla każdego x, y

Adam: Liczby naturalne 7, b, c tworzą ciąg rosnący. Nieznany wielomian o współczynnikach całkowitych przyjmuje dla tych argumentów odpowiednio wartości 77, 85, 0. Wyznaczyć b, c.

Mikojaj: Rozwiąże najpierw wszystkie zadania a nie ciągle wrzucanie nowe

Adam: taka była umowa, rozwiążesz zadanie, wrzucasz nowe i tyle

Mikojaj: To jakoś ta zasada została złamana bo nadal są nierozwiazane zadania

Rafal: Adma, b=9, c=14?

Adam: nie mam odpowiedzi, ale też mi tak wyszło

Rafal: OK Sorry za te literówki, od rana już tak mam.

Alka: Czemu podjęcie tylko same odpowiedzi

Rafal: A, przepraszam za moje roztargnienie. W ostatnim zadaniu Adama chodzi o rozważenie wyrażeń W(7)−W(b), W(b)−W(c), W(c)−W(7). Ze wzoru aⁿ−bⁿ=... możemy uzasadnić podzielność tych wyrażeń przez kolejno: 7−b, b−c, c−7, a ponadto wiemy, ile te wyrażenia są równe. Mamy: 7−b|−8, b−c|85, c−7|−77, skąd wyznaczamy b i c. Aha, marta, dasz jakąś wskazówkę do Twojego zadania, bo przez nie mix stoi w miejscu?

Rafal: Tymczasem kolejne zadanie mające bardzo krótkie rozwiązanie: Na bokach BC, CA i AB trójkąta ABC zbudowano po jego zewnętrznej stronie trójkąty równoboczne BCD, CAE i ABF. Wykazać, że AD = BE.

Kacper: Wsk. do zadania Marty. Podzielić na 2 części kąt 6 stopni i 66 oraz dwa pozostałe i każde liczyć z osobna

Kacper: Widzę, że zadanie Marty sprawiło sporo kłopotów

Rafal: No cóż... Łatwo idzie zapisać tę liczbę przy użyciu jedynie sin18 i cos18, a te wartości z kolei nietrudno wyliczyć. Kacper, masz jakieś ładniejsze rozwiązanie? I może niech ktoś wrzuci jakieś inne zadanie, bo mnie to osobiście załamało,

Kacper: Ja to zadanie zamieniłem na liczenie np cos72, ale nie jest to ładne rozwiązanie. Zadanko. Dany jest wielomian W(x)=x⁵+ax⁴+bx³+cx²+dx, a,b,c,d − rzeczywiste. Wiadomo, że W(1)=3, W(3)=7, W(5)=11 oraz W(7)=15. Oblicz w(4) Myślę, że bardzo łatwe

po prostu Michał: uklad rownan z 4 niewiadomymi?

Kacper: Kiepski pomysł

po prostu Michał: W(4) = 9

Adam: po prostu Michał, układ, czy inaczej?

mhmm: W W(1), W(3), W(5) i W(7) wartości funkcji rosną co 4. Między W(3), a W(5) też więc wzrost argumentu o 1 daje wzrostu wartości funkcji o 2, czyli W(4)=9 ?

Adam: mhmm, to jest przykład niepoprawnego wnioskowania

Mari: W(9)=19 ?

Mar: tutaj jest filmik z rozwiązaniem całej matury: https://www.youtube.com/watch?v=qrEHWpegKhI&t

Marcin: Zadanie Rafała trójkaty BCD oraz CAE są równoboczne. zachodzi równość miedzy kątami ECB=ACD zatem trójkąty EBC oraz ADC są przystajace. Czy ktoś moze pokazać rozwiązanie z tymi cosimusiami?

Adam: Marcin, przecież www podał link do rozwiązania

Marcin: Nie oglądałem sorry

Adam: nic się nie stało, spokojnie

Jack: Bez obliczenia. Zalozylem ze wartosci zmieniaja sie o 2 W(1) = 3 W(2) = 5 W(3) = 7 W(4) = 9 Itd.

Adam: Jack, właśnie chodzi o to że to jest błędny wniosek to nie jest niczym poparte

po prostu Michał: Jack, lepiej ukladem rownan, przynajmniej bedzie poparte

Adamm: w(4)=Aw(1)+Bw(3)+Cw(5)+Dw(7) 4⁴=A+3⁴B+5⁴C+7⁴D 4³=A+3³B+5³C+7³D 4²=A+3²B+5²C+7²D 4=A+3B+5C+7D 4³*3=3³*2B+5³*4C+7³*6D 4²*3=3²*2B+5²*4C+7²*6D 4*3=3*2B+5*4C+7*6D 4=A+3B+5C+7D 4*3*7=5*4*2*8C+7*6*4*10D 4*3=5*4*2C+7*6*4D 4*3=3*2B+5*4C+7*6D 4=A+3B+5C+7D −4*3=7*6*4*2D 4*3=5*4*2C+7*6*4D 4*3=3*2B+5*4C+7*6D 4=A+3B+5C+7D −1/28=D 9/20=C 3/4=B −1/4=A w(4)=312/35 ok?

Adamm: gdzieś się pomyliłem bo wynik wolframowy to 1572/35

Adamm: widocznie się nie pomyliłem, założyłem że to zadziała 4⁵=A+B*3⁵+C*5⁵+D*7⁵ ta równość nie jest spełniona po prostu szukałem prostszego rozwiązania niż rozwiązywanie układu

Kacper: Wynik to 45, szukajcie błędu

Krzysiek: Dany jest wielomian W(x)=x⁵+ax⁴+bx³+cx²+dx, a,b,c,d − rzeczywiste. Wiadomo, że W(1)=3, W(3)=7, W(5)=11 oraz W(7)=15. Oblicz w(4). W(x)−2x−1 ma pierwiastki 1,3,5,7, więc W(x)=(x−1)(x−3)(x−5)(x−7)(x−a)+2x+1 dla jakiejś liczby a. Wiemy, że W(0)=0 (−1)*(−3)*(−5)*(−7)*(−a)+1=0 z tego obliczamy a. −105a=0 a=0 W(x)=x(x−1)(x−3)(x−5)(x−7)+2x+1 W(4)=45

mania: Dla jakiego m f(x)=mx⁴−(m+2)x²+1 jest rosnąca w (−3,0).

rownania: Skąd wiemy że w(0)=0 i w opisie W(x) dlaczego zrobiłeś końcówkę 2x+1 i skąd wiesz że to Wielomian 5 stopnia A nie 4 lub 25?

AiO: Mania ja mysle ze tutaj jest miejsce na zadania tego typu Wieloscian wypukly jest calkowicie zawarty w szescianie o krawedzi 1 Udowodnij ze suma kwadratow pol scian tego wieloscianu nie przekracza 6 .

mania: Czemu moje zdanie nie jest jakiegoś typu

Kacper: rownania zobacz, że W(x) jest doprecyzowany którego jest stopnia i od razu widać, że jednym z pierwiastków jest 0.

Jack: Mania, nie sluchaj go

po prostu Michał: Kacper, skad wiadomo, ze trzbea odjac − 2x − 1 , w tamtym wielomianie? mania Dla jakiego m f(x)=mx⁴−(m+2)x²+1 jest rosnąca w (−3,0). f ' (x) = 4mx³ − 2(m+2)x f ' (x) > 0 4mx³−2(m+2)x > 0 x(4mx² − 2m − 4) > 0 to nie jest takie proste wbrew pozorom

AiO: Jack . Rozwiazania tego typu zadania znajdzie w internecie Wystarczy poszukac .Jest to zadanie schematyczne . A jak widzisz tutaj wstawiaja ludzie zadania nieschematyczne .

Kacper: Michał wystarczy zauważyć, że 3=2*1+1, 7=2*3+1 itd.

mania: o co chodzi z tym moim zadaniem "schematycznym"

Poloniusz: tylko że a≠0

po prostu Michał: AiO rozwiaz te zadanie skoro uwazasz ze schematyczne (czyt. latwe)

Rafal: Może czas trochę ruszyć z tym łańcuszkiem. Co do zadania mani, kluczowe jest pewnie zauważenie, że wykres funkcji f jest symetryczny względem osi OY. Przy założeniach, że f jest stopnia czwartego i jej pochodna ma trzy różne pierwiastki, to warunkiem dostatecznym i koniecznym, by warunki zadania zostały spełnione, jest to, by te dwa pierwiastki różne od zera były od tego zera oddalone co najmniej o 3 jednostki oraz by wykres funkcji miał ramiona zwrócone do dołu. Pozostałe przypadki dosyć łatwo idzie rozgryźć. Jako że nierówności cieszą się większym zainteresowaniem, to proponuję coś takiego (chyba Jensen, Cauchy−Schwarz i spółka tu nie działają, ale jest jedna metoda, która rozwala tę nierówność): Niech a,b,c,d będą liczbami rzeczywistymi dodatnimi i niech a+b+c+d=4. Wykaż, że

1		1		1		1		1
	+		+		+		≤		.
11+a2		11+b2		11+c2		11+d2		3

mania: Mozesz rozwiązać moje zadanie dokładniej ?

Rafal: A możesz podać odpowiedź?

mania: Wolałbym nie bo trzeba do niej dojść ale podpowiem ze przedził ograniczony plus jeszcze jedna lliczba

Rafal: Ehh, ma rosnąć w (−3,0), czyli w takim razie ramiona do góry. OK, nie chce mi się tego liczyć, bo w moim przypadku zawsze źle to się kończy, a nikt inny też się nie kwapi, więc chyba najlepiej będzie jednak podać tę odpowiedź i przejdziemy wtedy dalej.

Krzysiek: Rafał, nie powinien znak nierówności być w drugą stronę?

Rafal: Krzysiek, jest OK.

Adamm: chyba mam, ale nie jestem pewien i to nierównością Jensena biorąc funkcję f(x)=1/(11+x) i stosując dla a², b², c², d² dostajemy f([a²+b²+c²+d²]/4)≤f(a²)/4+f(b²)/4+...+f(d²)/4

16
	≤tamto
44+a2+b2+c2+d2

teraz ponownie biorąc g(x)=x² mamy g([a+b+c+d]/4)≤g(a)/4+...+g(d)/4 4≤a²+b²+c²+d²

16
	≤1/3
44+a2+b2+c2+d2

skąd mamy naszą nierówność

Adamm: nie, stój, to tak nie idzie

Rafal: Jakbyś się zbyt denerwował tą nierównością, to mogę ci podesłać pewien bardzo przydatny artykuł, który zresztą pewnie czytałeś

Krzysiek:

	12		12		12		12
4≥		+		+		+
	11+a2		11+b2		11+c2		11+d2

	1−a2		1−b2		1−c2		1−d2
0≥		+		+		+
	11+a2		11+b2		11+c2		11+d2

a2−1		b2−1		c2−1		d2−1
	+		+		+		≥0
11+a2		11+b2		11+c2		11+d2

Nierówność Cauchy'ego−Schwarza

	a2−1		b2−1		c2−1		d2−1
(		+		+		+		)(1+1+1+1)
	11+a2		11+b2		11+c2		11+d2

	√a2−1		√b2−1		√c2−1
≥(		+		+		+
	√11+a2		√11+b2		√11+c2

√d2−1
	)2≥0
√11+d2

Rafal: Krzysiek, ale skąd wiesz, że te pierwiastki istnieją?

Krzysiek: kurcze, myślałem że nie zauważysz xD

Rafal:

Rafal: Chcecie podpowiedź?

Adamm: nie

mania: Rafał ale mój sposób jest zupełnie inny I to zadanie było na maturze

Krzysiek: już wiem jak to zrobić

Rafal: mania, to wrzuć rozwiązanie

mania : Może ktoś się w końcu pokusić bo to chyba nie na tym polega aby rozwiązywać je samemu

Rafal: To chociaż odpowiedź, to sprawdzę, czy mi dobrze wyszło. Pewnie źle, więc proszę najpierw Ciebie.

mania : Ok [0;0,4] i jeszcze 2

Rafal: Hmm... dla m=−1 mamy f(x)=−x⁴−x²+1, a ona rośnie (−3,0).

Krzysiek:

a2−1		b2−1		c2−1		d2−1
	+		+		+		≥0
11+a2		11+b2		11+c2		11+d2

(a−1)(a+1)		(b−1)(b+1)		(c−1)(c+1)		(d−1)(d+1)
	+		+		+		≥0
11+a2		11+b2		11+c2		11+d2

Nierówność Jensena

	x−1
f(x)=
	11+x2

a₁=a+1, x₁=a a₂=b+1, x₂=b a₃=c+1, x₃=c a₄=d+1, x₄=d

	a2+b2+c2+d2+a+b+c+d		a2+b2+c2+d2+a+b+c+d   −1 8
L≥8f(		)=8
	8		11+(...)2

	a2+b2+c2+d2+a+b+c+d   −1 8
8		≥0
	11+(...)2

a²+b²+c²+d²+a+b+c+d≥8 a²+b²+c²+d²≥4 Nierówność Cauchego−Schwarza (a²+b²+c²+d²)(1+1+1+1)≥(a+b+c+d)²=16

Adamm: może tak a+b+c+d=4 4≤a²+b²+c²+d²

	1		1
chcemy by		+...+		było jak największe, a jest gdy a2, ..., d2 są
	11+a2		11+d2

jak najmniejsze jeśli a²+...+d²=x≥4 to zawsze możemy zmniejszyć jedno z a², ..., d² pomniejszając tą zarówno tą sumę, tym samym zwiększając tamtą, i jeśli a², ..., d² są najmniejsze to a²+b²+c²+d²=4 ale równość zachodzi tylko gdy a=b=c=d=1

	1		1
sprawdzamy że wtedy suma		+...+		jest równa 1/3
	11+a2		11+d2

Rafal: OK, muszę to ogarnąć, ja korzystałem (za wskazówką) z metody stycznych: http://www.deltami.edu.pl/temat/matematyka/analiza/2013/01/30/Nierownosci_i_styczne/

Adamm: Rafal, to jest ten artykuł? co prawda czasami się natknę, ale nie czytam często

Rafal: tak, bardzo rozwijający, polecam

Adamm: Rafal, może pora już założyć nowy temat? bo dobijamy do 200 postów

Rafal: A proszę https://matematykaszkolna.pl/forum/353268.html

Kacper: Niestety, do mojego zadania wkradła się literówka, wielomian jest postaci W(x)=x⁵+ax⁴+bx³+cx²+dx+1 Rozwiązanie Krzyska jest też niestety niepoprawne (do wersji bez 1). Do wersji z 1 byłoby prawie dobre, tzn wynik dobry. Gdy na końcu nie ma 1 sprawa się komplikuje. Pozostaje kalkulator.

	1572
Adam podał prawidłowy wynik dla tamtego wielomianu W(4)=		.
	35

Rafal: Adamm, wybacz, jeśli to banalne pytanie, ale czy Twoje rozumowanie nie działa tylko wtedy, gdy wiemy, że a², b², c², d² są ≥1?

Adamm: czemu miałoby nie działać? nie rozumiem

Rafal: A co jeśli weźmiemy bardzo małe a i dosyć duże b, c, d? Suma kwadratów będzie większa, ale może funkcja przyjmie wtedy większą wartość. To takie moje, być może głupie, wątpliwości.

Adamm: właściwie to sam nie wiem wiesz, w mojej głowie przez chwilę to miało sens

Rafal: Jasne, i tak wiesz więcej ode mnie. Może źle się wyraziłem: zmniejszając jedno, musisz zwiększyć drugie, bo ich suma jest stała.

Daria: Tu jest podobne https://www.matematyka.pl/136565.htm#p511075 Następne niech będzie moje https://matematykaszkolna.pl/forum/353277.html

Rafal: A co z tym m=−1?

po prostu Michał: Moze, nie za trudne zadanko na dowodzenie. a+b+c = 1 udowodnij, ze a²+b² + c² + 2√3abc ≤ 1

po prostu Michał: oraz drugie, jeszcze prostsze (2) Udowodnij, ze dla liczb dodatnich a,b zachodzi nierownosc. 2(a²+b²) ≥ (a+b)²

po prostu Michał: dobra, to drugie to zbyt banalne, pomylilem z innym ;

Kuba: Męczę się z tym zadaniem manii , moze ktoś popkaze pełne rozwiązanie

kochanus_niepospolitus: Chodzi Ci o: Dla jakiego m f(x)=mx⁴−(m+2)x²+1 jest rosnąca w (−3,0) no to jedziemy: D_f = R f'(x) = 4mx³ − 2(m+2)x = x (4mx² − 2(m+2) ) skoro ma być rosnąca w przedziale (−3,0) to f'(−3) = 0 i f'(0) = 0 oraz f'(x) > 0 dla x∊(−3,0) f'(x) = x (4mx² − 2(m+2) ) ⇒ x = 0 ; 4m(−3)² − 2(m+2) = 0 4m(−3)² − 2(m+2) = 0 ⇔ 36m − 2m − 4 = 0 ⇔ m = ... i sprawdzasz czy dla takiego 'm' zachodzi: f'(x) > 0 dla x∊(−3,0)

Kuba: Jak jest w końcu odpowiedz do tego zadania?

kochanus_niepospolitus:

	2
34m = 4 −> m =
	17

Kuba: Kuba tylko m=2/17 spełnia warunki tego zadania?

kochanus_niepospolitus: https://www.wolframalpha.com/input/?i=(2%2F17)x%5E4-(2%2B2%2F17)x%5E2%2B1+from+-4+to+1

Kuba: To jest az tak trudne zadanie

kochanus_niepospolitus: nie ... jak trudne? toć Ci to rozwiązałem ... rozwiązanie tego zadania trwa (może) minutę

Kuba: No to jaka jest odpowiedz poprawna bo tyle juz tu napisano że w końcu sie pogubiłem

Rafal: Może tak: Mamy f'(x)=2x(2mx²−m−2). Jeśli m=0, to f(x)=−2x²+1, czyli OK. Jeśli zaś m≠0, to: 1) gdy Δ<0, czyli m∊(−2,0), to wykres funkcji ma ramiona zwrócone do dołu, drugi czynnik w pochodnej stale ujemny, więc funkcja f rośnie w (−∞,0> i maleje w <0,+∞), czyli OK. 2) gdy Δ=0, czyli m=−2, to f(x)=−2x⁴+1, czyli OK 3) gdy Δ>0, czyli m∊(−∞,−2)∪(0,+∞), to funkcja f ma trzy różne ekstrema: jedno z nich jest w punkcie 0, a dwa pozostałe są symetryczne względem 0 ze względu na parzystość funkcji f. W tym przypadku warunki zadania będą spełnione wtedy i tylko wtedy, gdy ramiona będą skierowane do góry, a ekstrema będą oddalone od 0 co najmniej o 3 jednostki. Aby tak było, trzeba i wystarczy wziąć m>0 i x₁x₂≤−9 (ze względu na symetrię). Ostatecznie dostajemy tu przedział

	2
(0,		>.
	17

Mógłby ktoś sprawdzić?

Kuba: Rafał a sam pisałeś że − 1 też spełnia warunki zadania hmmm

Rafal: No i spełnia, bo te wszystkie przedziały trzeba zsumować.

Kuba: Czy takie zadanie może być na maturze czy nie?

Rafal: Raczej wielu by na tym poległo, ale na zeszłorocznej planimetrii też większość poległa. więc...

Kuba: To moze jakiś student to rozwiąze tutaj

kuba: AiO możesz pokazać rozwiązanie tego zdania! Wieloscian wypukly jest calkowicie zawarty w szescianie o krawedzi 1 Udowodnij ze suma kwadratow pol scian tego wieloscianu nie przekracza 6 .

kuba: ponawiam