matura
Daria: Dany jest ostrosłup ABCD o podstawie ABC. Podstawa ABC jest trójkątem równobocznym o boku a.
Wiadomo także że kąty ADC=x, ADB=y oraz BDC=y .
Oblicz długość odcinka DE jeśli E to środek ogregu opisanego na ABC.
7 maj 11:24
Daria: Sory powinno być BDC=z
7 maj 13:22
Daria: Nikt nie umie?
7 maj 17:33
Mila:
Nic nie wiadomo o kątach, to cała treść?
7 maj 20:25
kochanus_niepospolitus:
W obecnej formie to z pewnością nie jest zadanie maturalne.
Teoretycznie ilość danych wystarczy na podanie długości odcinka DE, jednak same przekształcenia
z całą pewnością przekraczają poziom dzisiejszego licealisty.
7 maj 20:29
Daria: Czemu?
7 maj 20:32
kochanus_niepospolitus:
ponieważ długość AD, BD, CD będą podane jako funkcje zmiennej 'a' oraz cosinusa odpowiedniego
tam kąta.
te długości później posłużą do obliczenia długości wysokości tegoż ostrosłupa, (oraz
usytuowania jego rzutu na podstawę) co ostatecznie pozwoli wyznaczyć długość DE,
jednak tak jak pisałem ... to z całą pewnością nie jest poziom obecnego licealisty.
Baaa ... większość tegorocznych inżynierów by nie podołała temu zadaniu.
7 maj 20:57
Mila:
A skąd masz to zadanie?
7 maj 21:35
Daria: Czy wy sobie zartujecie
7 maj 22:38
kochanus_niepospolitus:
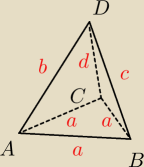
z tw. cosinusów:
a
2 = b
2 + c
2 − 2bc*cosy
a
2 = b
2 + d
2 − 2bd*cosx
a
2 = c
2 + d
2 − 2cd*cosz
niewiadome to b,c,d ... mamy układ trzech równań z trzema niewiadomymi ... tak więc, możemy
wyznaczyć b,c,d
jednak będzie to 'szalenie mozolne' (co nie oznacza, że jest to niemożliwe).
7 maj 22:38
kochanus_niepospolitus:
to nie my dajemy zadanie w którym można się po prostu zagrzebać w obliczeniach (co zwiększa
szansę na popełnienie głupiego błędu).
Z całą pewnością tego zadania nie rozwiąże się w 10 min ... dla licealisty pół godziny to
minimum.
7 maj 22:40
Daria: Jak pół godziny, przesadzić może jeszcze napiszecie że to zadanie dla matematykow
7 maj 23:00
kochanus_niepospolitus:
to Dario ... skoroś taka 'szybka' to proszę mi tutaj wyznaczyć b,c,d w zależności od zmiennych:
(a, cosx, cosy, cosz)
masz na to 10 minut.
7 maj 23:01
kochanus_niepospolitus:
czas minął ... więc co ... nadal sądzisz: 'jak pół godziny'


| | 1 | |
A wyznaczenie b,c,d to zaledwie |
| zadania |
| | 3 | |
7 maj 23:14
Daria: Widze ze macie zabawe z tymi co nie umieją rozwiązać zadania
7 maj 23:29
vxxx:
Po pierwsze Daria nie bredzić, nie odpowiedziałaś na zadane pytania. Treść jest nietypowa,
bo nic nie wiadomo o kątach.
Jeśli masz to ze zbioru to sprawdź , czy nie ma innych informacji.
7 maj 23:36
kochanus_niepospolitus:
Daria ... zrozum ... w takiej formie to zadanie jest do rozwiązania, ale z całą pewnością nie
jest to zadanie na poziomie MATURALNYM

Tak naprawdę, ja sam bym musiał tutaj siedzieć niemało czasu nad przekształceniami i samo
zadanie by nie zostało 'od tak' rozwiązane, pomimo że posiadam w głowie sposób na jego
rozwiązanie (nawet przy braku konkretnych danych − czyli w tej właśnie formie).
Co więcej − sposób w jaki bym to rozwiązał jest tak na prawdę 'na pograniczu' wiedzy licealnej,
co za tym idzie − takie zadanie nie znalazłoby się na maturze.
Jeżeli to zadanie masz z jakiegoś zbioru to podaj nazwę tego zbioru. Jeżeli to zadanie 'ktoś
wymyślił' to niech ten ktoś się puknie w głowę

7 maj 23:40
Daria : Kąty są podane wynoszą x,y,z. A jaki w takim raziem poziom tego zdania uważacie/

7 maj 23:43
vxxx:
I co jeszcze wiadomo o kątach? Z jakiego zbioru?
7 maj 23:51
Daria: Tylko tyle ze są dane jako x,y,z
7 maj 23:52
kochanus_niepospolitus:
Daria ... cholera jasna ... zrozum ... że samo wyznaczenie długości boków tego ostrosłupa
(uzależnione od długości podstawy i cosinusów danych kątów przy wierzchołku) jest czymś z czym
sobie nie poradzą ludzie uczący się matematyki.
Fakt, że nie masz podanych żadnych KONKRETNYCH wartości sprawia, że obliczenia są tragiczne. To
także powoduje dodatkowy problem w podejściu do samego rozwiązania.
Skoro nadal nie chcesz podać zbioru zadań, to widzę, że to zadanie sama wymyśliłaś.
PS.
Może ktoś ma jakiś inny pomysł na rozwiązanie tego zadania, ja tu widzę konieczność
umieszczenia tego ostrosłupa w przestrzeni (niech wierzchołek A będzie w punkcie (0,0,0)) i
wyznaczenie punktu D jako punktu przecięcia się trzech kul o promieniach b,c,d ze środkami w
wierzchołkach A,B,C.
Mając współrzędne wierzchołka D już jest z górki, bo współrzędne punktu E wyznacza się bardzo
prosto i lecimy ze wzoru na długość odcinka.
7 maj 23:52
Daria: Nie wymyślone przeze mnie aż taka zdolna nie jestem. Dostałam to od nauczyciela jako jedno z
wielu zdań do przygotowania.
7 maj 23:55
kochanus_niepospolitus:
to niech się nauczyciel puknie w czerep i sam rozwiąże to zadanie.
Ciekaw jestem jak będzie marszczył brwi gdy będzie miał wyznaczyć długości boków tego
ostrosłupa.
Chyba że po prostu źle zapisałaś zadanie.
7 maj 23:57
Daria: To było wydrukowane i taka jest treść.
7 maj 23:59
kochanus_niepospolitus:
To idź jutro do nauczyciela i niech Ci pokaże jak rozwiązać to zadanie.
Należy pamiętać, że skoro kąty rozwarcia ścian są różne to rzut punktu D (na płaszczyznę
podstawy ostrosłupa) nie pokrywa się z żadną wysokością tegoż trójkąta (podstawa ostrosłupa).
8 maj 00:01
Daria: To w takim razie takie zadania rozwiązuje sie na studiach?
8 maj 00:05
kochanus_niepospolitus:
jeszcze raz Ci napiszę:
TAKIE PRZEKSZTAŁCENIA SPRAWIĄ PROBLEMY NAWET OBECNYM INŻYNIEROM MATEMATYKI STOSOWANEJ

Ja, gdybym musiał to zrobić, to bym zrobił ... ale szczerze mówiąc, jest to taka straszna
mordęga z obliczeniami, że gra jest niewarta świeczki.
Jeszcze raz napiszę −−− idź do nauczyciela i niech on Ci pokaże jak wyznacza długości boków
AD,BD,CD (rozwiązując to przy Tobie).
Jeżeli treść zadania faktycznie tak miała wyglądać, to gwarantuje, że będzie mu się głowa
dymiła w momencie wyznaczania tychże długości.
8 maj 00:08
vxxx:
Popieram. Zadanie w tej formie bez sensu.
Chyba, że masz pod spodem , małym druczkiem
x=..., y=.. z=.. i konkretne wartości np. x=y=z=90
8 maj 00:23
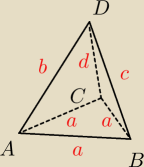 z tw. cosinusów:
a2 = b2 + c2 − 2bc*cosy
a2 = b2 + d2 − 2bd*cosx
a2 = c2 + d2 − 2cd*cosz
niewiadome to b,c,d ... mamy układ trzech równań z trzema niewiadomymi ... tak więc, możemy
wyznaczyć b,c,d
jednak będzie to 'szalenie mozolne' (co nie oznacza, że jest to niemożliwe).
z tw. cosinusów:
a2 = b2 + c2 − 2bc*cosy
a2 = b2 + d2 − 2bd*cosx
a2 = c2 + d2 − 2cd*cosz
niewiadome to b,c,d ... mamy układ trzech równań z trzema niewiadomymi ... tak więc, możemy
wyznaczyć b,c,d
jednak będzie to 'szalenie mozolne' (co nie oznacza, że jest to niemożliwe).


 Tak naprawdę, ja sam bym musiał tutaj siedzieć niemało czasu nad przekształceniami i samo
zadanie by nie zostało 'od tak' rozwiązane, pomimo że posiadam w głowie sposób na jego
rozwiązanie (nawet przy braku konkretnych danych − czyli w tej właśnie formie).
Co więcej − sposób w jaki bym to rozwiązał jest tak na prawdę 'na pograniczu' wiedzy licealnej,
co za tym idzie − takie zadanie nie znalazłoby się na maturze.
Jeżeli to zadanie masz z jakiegoś zbioru to podaj nazwę tego zbioru. Jeżeli to zadanie 'ktoś
wymyślił' to niech ten ktoś się puknie w głowę
Tak naprawdę, ja sam bym musiał tutaj siedzieć niemało czasu nad przekształceniami i samo
zadanie by nie zostało 'od tak' rozwiązane, pomimo że posiadam w głowie sposób na jego
rozwiązanie (nawet przy braku konkretnych danych − czyli w tej właśnie formie).
Co więcej − sposób w jaki bym to rozwiązał jest tak na prawdę 'na pograniczu' wiedzy licealnej,
co za tym idzie − takie zadanie nie znalazłoby się na maturze.
Jeżeli to zadanie masz z jakiegoś zbioru to podaj nazwę tego zbioru. Jeżeli to zadanie 'ktoś
wymyślił' to niech ten ktoś się puknie w głowę 

 Ja, gdybym musiał to zrobić, to bym zrobił ... ale szczerze mówiąc, jest to taka straszna
mordęga z obliczeniami, że gra jest niewarta świeczki.
Jeszcze raz napiszę −−− idź do nauczyciela i niech on Ci pokaże jak wyznacza długości boków
AD,BD,CD (rozwiązując to przy Tobie).
Jeżeli treść zadania faktycznie tak miała wyglądać, to gwarantuje, że będzie mu się głowa
dymiła w momencie wyznaczania tychże długości.
Ja, gdybym musiał to zrobić, to bym zrobił ... ale szczerze mówiąc, jest to taka straszna
mordęga z obliczeniami, że gra jest niewarta świeczki.
Jeszcze raz napiszę −−− idź do nauczyciela i niech on Ci pokaże jak wyznacza długości boków
AD,BD,CD (rozwiązując to przy Tobie).
Jeżeli treść zadania faktycznie tak miała wyglądać, to gwarantuje, że będzie mu się głowa
dymiła w momencie wyznaczania tychże długości.