mix Rafal: Łańcuszek część II (1) Jaka jest dokładna wartość liczby tg9−tg27−tg63+tg81? Wiem, że rozwiązanie łatwo znaleźć w necie, ale jakby ktoś chciał się sprawdzić, to... warto spróbować!

dora: zamieniając to na sin/cos mamy tg 9 − tg 27 − tg 63 + tg 81=tg9−tg27−ctg(90−27)+ctg(90+9)=tg9−tg27−ctg27+ctg9

	sin(9−27)		sin(27−9)
=		+		=
	cos9cos27		sin9sin27

	(−sin9sin27+cos9cos27)		4sin18cos36
=sin18		=		=
	1   sin2*9sin2*27 4		sin54sin18

4.cos36
	=4
cos(90−54)

Czworościan foremny o krawdzi a przecięto płaczyzną równoległa do dwóch skośnych krawędzi i przechodzacą w odległośc 0,5a od jednej z tych krawędzi. Oblicz objętość brył otrzymanych w wyniku tego przecięcia.

Kacper: Sprytnie zrobione

AiO: Takim zadaniem pograzyliby bardzo duzo maturzystow .

Rafal: https://www.geogebra.org/m/JQ3gCfbU Wydaje mi się, że wystarczy zapisać długości boków zielonego trapezu za pomocą a i jakieś zmiennej, np. x, i skorzystać z tego, że wysokość to 0,5 a. Stąd wyliczymy x, a potem objętość graniastosłupa trójkątnego itd.

Rafal: Ale radzę poczekać na Milę i Etę

dora: Rafał ale jeszcze trzeba to policzyć....A ty tez zdajesz mature?

Rafal: dora, wiem, ale nie cierpię zadań tego typu, dlatego czekam jedynie, aż ktoś potwierdzi ideę. Co do drugiego pytania, to tak, ale im bliżej, tym bardziej zaczynam wątpić w swoje możliwości.

Rafal: Całkiem fajne zadanko: Punkt H jest punktem przecięcia wysokości trójkąta ostrokątnego ABC. Wykazać, że punkty symetryczne do punktu H względem prostych AB, BC, CA leżą na okręgu opisanym na trójkącie ABC. Niektórzy się już pewnie domyślają, skąd te zadania biorę

AiO: Czy z zadan Pana doktora Pompe ?

Rafal: AiO, tak jest, czyżbyś był olimpijczykiem?

AiO: Rafal nie . Ale pisalem do Pana doktora

Kacper: Dobrze pamiętam skąd te zadanka

AiO: Napisal tez ksiazeczke pt Wokol obrotow −przewodnik po geometrii elementarnej (str47

moje: https://www.google.pl/url?sa=t&rct=j&q=&esrc=s&source=web&cd=3&cad=rja&uact=8&ved=0ahUKEwi3sJOuwN3TAhUMDywKHSyaAKwQFggwMAI&url=https%3A%2F%2Fwww.ore.edu.pl%2Fcomponent%2Fphocadownload%2Fcategory%2F127-poradniki%3Fdownload%3D2180%3Arozszerzony-program-matematyki-dla-gimnazjum.-poradnik-nauczyciela-matematyki&usg=AFQjCNE4LzAVyIoYR2nEmbc5brX7kAoJ3g&sig2=Nl6n-p74JQuMWEbGbGrrPw str328

Rafal: Są bardzo rozwijające. Po przerobieniu ich człowiek zaczyna myśleć bardziej niestandardowo − może by tu dorysować równoległobok, może gdzieś jest ukryty okrąg, a może trójkąty przystające. Chociaż znając życie, zadania z planimetrii i tak nie zrobię na maturze

dora: A ktoś rozwiąże to z czworościanem do końca tak jak zaproponował Rafał?

AiO: A to Ty nie jestes MrComandore (czy jakos tam ? )

Kacper: Mam tę książeczkę w wersji drukowanej

Rafal: up

Adamm: wyznaczyć wszystkie funkcje monotoniczne f:ℛ→ℛ, że dla dowolnych x, y∊ℛ zachodzi f(f(x)−y)+f(x+y)=0

Kacper: To nie jest zadanie z któregoś OM−a? Gdzieś mi się kojarzy.

Adamm: dokładnie

Adamm: wyszło mi f(x)=0 lub f(x)=−x

Kacper: To średnio na zadanie maturalne.

Adamm: wiem, ale chciałem dać jakieś zadanie z równaniem funkcyjnym

Adamm: ktoś chce samemu czy napisać rozwiązanie?

Rafal: A napisz, chętnie poczytam.

gusto: Czy ktoś umie to https://matematykaszkolna.pl/forum/353279.html

Adamm: zakładam że chodzi o ścisłą monotoniczność niech w naszym równaniu y=f(x) f(x+f(x))=−f(0) jeśli ciąg jest stały, to musi być f(x)=0 jeśli ciąg nie jest stały, to jedyna opcja by x+f(x) było stałe f(x)=c−x i podstawiając znajdujemy c=0 stąd f(x)=−x oraz f(x)=0 to jedyne rozwiązania

Adamm: Znaleźć takie trzy liczby, których suma, a także suma każdej pary tych liczb jest kwadratem innej liczby

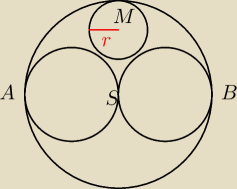
Adamm: to było bardziej zagadka, teraz jakieś bardziej maturalne Dany jest okrąg o średnicy AB oraz środku S, oraz dwa okręgi o średnicach AS i BS. Okrąg o środku M i promieniu r ma z każdym z danych okręgów dokładnie jeden punkt

	1
wspólny. Wykaż że r=		|AB|
	6

Rafal: Adamm Mamy trójkąt równoramienny o bokach długości R+r, R+r, 2R, gdzie R to długość promieni tych "średnich" okręgów. Wysokość tego trójkąta opuszczona na podstawę ma długość 2R−r − z twierdzenia Pitagorasa dostajemy tezę. Bezczelnie zerżnąłem z matematyka.pl, ale jest fajne: Wykazać, że jeżeli a,b,c są długościami boków trójkąta oraz odpowiednio kąty α, β, γ leżą naprzeciwko tym bokom, a także S to pole tego trójkąta, to zachodzi:

	a2+b2+c2
ctgα+ctgβ +ctgγ =		.
	4S

Rafal: Co do zagadki: czy rozwiązaniem są permutacje trójki (−n,0,n)?

kochanus_niepospolitus: Rafał ... −n + 0 nie jest kwadratem żadnej liczby (naturalnej − przyp. red.)

Rafal: No tak, przepraszam, nie myślę już dzisiaj. Spojrzałem tylko na pierwszą równość. Pewnie musi być (0,0,0).

Rafal: W ogóle mam problemy z czytaniem treści, np. nie zauważyłem słowa "monotoniczne" w zadaniu Adamma i przez pół godziny siedziałem nad nim, bez żadnych efektów oczywiście. A tak przy okazji, mam wątpliwości co do rozwiązania zadania mani: skąd wiadomo, że w −3 jest ekstremum? Jest powiedziane, że funkcja rośnie w (−3,0), ale jeśli rośnie w (−5,0), to też jest OK, no chyba, że znowu czegoś nie widzę.

kochanus_niepospolitus: masz rację ... to była moja nadinterpretacja w tamtym zadaniu

kochanus_niepospolitus: taki liczb jest całkiem sporo, mamy chociażby taką rodzinę: (0,9,16) (0,25,144) (0,49,576) itd.

	(2n+1)2 − 1
ogólnie: (0, (2n+1)2, (		)2 ) ; gdzie n∊N+
	2

kochanus_niepospolitus: takich*

kochanus_niepospolitus: Twój zestaw Rafał jest niewłaściwy ... bo mają być kwadraty RÓŻNYCH liczb

Rafal: O, myślałem, że ma zachodzić coś w stylu: a+b=c², b+c=a² itd. Znowu nie myślę.

kochanus_niepospolitus: a samo rozwiązanie wynika z tego co zauważył jeden ze sławnym matematyków już za młodych (swych) lat: "Suma 'n' kolejnych liczb nieparzystych zawsze da kwadrat jakieś liczby naturalnej' Co było wnioskiem z zabawy z klockami i dokładaniu do już ułożonych kloców kolejnego zestawu i tworzeniu dzięki temu większego kwadrata. Zdając sobie z tego sprawę, zacząłem szukać takich liczb nieparzystych p>1, które będą kwadratem liczby nieparzystej (no i mamy 9). Kwadrat, który ów dziewiątka 'oplata' jest kwadratem liczby naturalnej, a suma tych dwóch liczb także da kwadrat liczby naturalnej. Pozostało więc dorzucić trzecią liczbę = 0, co by każda z sum była kwadratem jakiejś liczby.

Rafal: O, ciekawe, a co to za matematyk? kochanus_niepospolitus, rzucisz okiem na moje rozwiązanie zadania mani?

gusto: Stosując twierdzenie cosinusów i dodając stronami dostaniemy: że a²+b²+c²=2abcosγ+2bccosα+2accosβ Teraz zauwazmy ze

	cosγ		1
2abcosγ=2		*ab*sinγ=2ctgγ*absinγ=2ctgγ*2*		absinγ=4ctgγ*S i postępujac tak
	sinγ		2

analogicznie Podstawiamy to do pierwszej równośći i mamy tezę. Następne.... W trójkacie ABC, H jest punktem przecięcia wysokości, P jest punktem przecięcia AH oraz BC, R jest promieniem okręgu opisanego, Wykaż że (a) AH = 2R cosA, (b) HP=2R cosB cos C

Adamm: ok, wszystko w porządku, treść zagadki jest po prostu niedoprecyzowana w zadaniu chodzi o liczby naturalne, ale dodatnie

Adamm: w zagadce możecie podać konkretną trójkę

Rafal:

	a		a
(a) Z tw. sinusów		=2R, więc trzeba pokazać, że AH=		*cosα=AH*ctgα, a to
	sinα		sinα

wprost z definicji.

Rafal: ehh, miało być a*ctgα.

PUNK1: Czy moze ktos rozwizać to ostatnie zadanie

Eta: Napisz treść tego zadania w nowym poście!

Wika: Może by taki łańcuszek w tym roku do matury zrobic?