kontynuacja
Adamm: rozwiąż równanie
(x2−5x+6)2−5(x2−5x+6)+6=x
rozwiąż układ równań
x+y+z=1
xy+xz+yz=−5
xyz=−5
rzucamy sześcienną kostką do gry aż do wylosowania szóstki
oblicz prawdopodobieństwo wylosowania piątki
29 kwi 16:48
Kacper:
Dla kogo to?
29 kwi 17:08
Adamm: dla tego kto chce rozwiązać zadanie
29 kwi 17:08
5-latek: Kacper 
maturzystow
29 kwi 17:09
matura 2017:
1/(x
2−5x+6)
2−4(x
2−5x+6)+4=
x2−5x+6 +x−2
(x
2−5x+4)
2=(x−2)
2
..............................
i teraz już z górki

29 kwi 17:13
Rafal: Może ustalmy, że każda osoba, która rozwiąże zadanie, wrzuca nowe − powstanie wtedy taki
łańcuszek maturalny

Co do rozwiązań, to może lepiej będzie podawać jedynie pomysły, żeby każdy mógł je zrobić
samodzielnie.
Tak więc:
1) jeśli f(x)=x, to f(f(x))=f(x)=x − w ten sposób znajdujemy dwa pierwiastki, potem wymnażamy
wszystko, dzielimy itd.
2) wzory Viete'a dla wielomianu stopnia trzeciego
3) n rzutów, w pierwszych n−1 za każdym razem możemy dostać 5 wyników, prawdopodobieństwo, że 5
| | 4n−1 | |
nie wypadnie ani razu: |
| |
| | 5n−1 | |
Jest OK? Jeśli tak, do dajcie znać, a coś wrzucę.
29 kwi 17:18
matura 2017:
trygonometria
zad1Rozwiąż równanie:
29 kwi 17:21
Adamm: 1) ok
2) ok
3) ... nie wiem co powiedzieć, zadanie nie skończone

29 kwi 17:21
Rafal: Potem wzór na prawdopodobieństwo przeciwne

29 kwi 17:22
Rafal: Łapcie fajne zadanko z tegorocznego finału konkursu PW:
Znajdź wszystkie rozwiązania równania:
| | 1 | | 3x | | 7 | |
4cos4(x)−cos(2x)− |
| cos(4x)+cos( |
| )= |
| |
| | 2 | | 4 | | 2 | |
Tu link do pozostałych:
https://konkurs.mini.pw.edu.pl/node/12987
29 kwi 17:28
Rafal: | | 1−tg2(x) | |
matura 2017, czy chodzi tu o podstawienie cos(2x)= |
| ?  |
| | 1+tg2(x) | |
29 kwi 17:36
matura 2017:
Możesz ......... ale jest krótszy sposób

29 kwi 17:38
Przyszłymakler: jak widzę pierwiastek z trzech to myślę tylko o dzieleniu przez 2 XD
29 kwi 17:50
Rafal: Skąd ja to znam

29 kwi 17:51
matura 2017:
Ciepło, ciepło ..... ale jeszcze za wcześnie

Najpierw ładne przekształcenia i założenia!
Myślcie dalej..........................

29 kwi 17:52
matura 2017:
Jak idzie?

29 kwi 17:58
Rafal: Coś dzisiaj nie myślę. Na razie mam tyle:
.
29 kwi 18:02
StrasznyNieogar: Adamm skąd masz takie super zadania typu to pierwsze?
(x2−5x+6)2−5(x2−5x+6)+6=x
29 kwi 18:03
matura 2017:
Ładne zadanko

Myślcie dalej............
29 kwi 18:04
matura 2017:
Masz podobne:
(x
2−5x−2)
2−5(x
2−5x−2)= x+2

29 kwi 18:10
Mariusz:
x+y+z=1
xy+xz+yz=−5
xyz=−5
To są wzory Vieta dla wielomianu trzeciego stopnia
t3−t2−5t+5=0
t3−5t−t2+5=0
t(t2−5)−1(t2−5)=0
(t−1)(t2−5)=0
(t−1)(t−√5)(t+√5)
Rozwiązaniem są permutacje ciągu
(√−5,1,√5)
29 kwi 18:14
Mariusz:
*minus oczywiście jest poza pierwiastkiem
29 kwi 18:15
Adamm: StrasznyNieogar, raz widziałem podobne, wymyśliłem
29 kwi 18:17
matura 2017:
@
Adamm −−− "złap się" za to równanie
trygonometryczne 
29 kwi 18:23
StrasznyNieogar: super Adamm, takie przekształcenia sprawiają mi największą frajdę, a jednocześnie są dla mnie
duzym problemem. Taka sprzeczność

29 kwi 18:26
29 kwi 19:02
Adamm: oczywiście to równanie 17:21
29 kwi 19:04
Adamm: tgx≠tg(−π/3)
x≠−π/3+kπ, k∊ℤ
cosx≠0
x≠π/2+kπ
sinx+2cos2xcos(x−π/6)=0
sinx+cos(x+π/6)+cos(3x−π/6)=0
cos(π/6−x)=−cos(3x−π/6)
cos(π/6−x)=cos(3x+5π/6)
...
x=−π/6+kπ/2
29 kwi 19:09
Adamm: Rafal, jakaś podpowiedź to tego równania, czy kombinować aż wyjdzie?
29 kwi 19:18
Rafal: Z tego, co pamiętam, to trzeba było rozpisać maksymalnie cos(4x), potem coś się skróciło i
dostaliśmy jakiś przypadek skrajny.
29 kwi 19:23
Adamm: do drugiego wyszło mi
x=8kπ, k∊ℤ
dobrze? trochę dziwne rozwiązanie
29 kwi 19:25
Adamm: | | 1 | | 3 | | 7 | |
4cos4x−cos2x− |
| cos4x+cos |
| x= |
| |
| | 2 | | 4 | | 2 | |
cos
22x=(2cos
2x−1)
2=4cos
4x−4cos
2x+1
| | 1 | | 3 | | 9 | |
cos22x+4cos2x−cos2x− |
| cos4x+cos |
| x= |
| |
| | 2 | | 4 | | 2 | |
x=8kπ
29 kwi 19:30
matura 2017: Ok
Inny sposób

Równanie :
| tgx | |
| +cos(2x)=0 założenia ..... |
| √3+tgx | |
cos(2x)(
√3+tgx)+tgx=0 i z tożsamości : cos2x= sin2x −tgx ( do wyprowadzenia)
√3cos2x+sin2x=0 /:2
29 kwi 19:31
Rafal: Mi wyszło tyle samo.
cos(4x) = 2cos
2(2x)−1 = 2(2cos
2(x)−1)
2−1 = 8cos
4(x)−8cos
2(x)+1
| 1 | | 1 | |
| cos(4x) = 4cos4(x)−4cos2(x)+ |
| |
| 2 | | 2 | |
| | 1 | | 3x | | 7 | |
−cos(2x)+4cos2(x)− |
| +cos( |
| ) = |
| |
| | 2 | | 4 | | 2 | |
| | 3x | |
1−2cos2(x)+4cos2(x)+cos( |
| ) = 4 |
| | 4 | |
29 kwi 19:41
29 kwi 19:43
Rafal: To tak na marginesie

Aby łańcuszek nie stanął:
Punkt O jest środkiem okręgu opisanego na trójkącie ostrokątnym ABC. Punkt D jest rzutem
prostokątnym punktu C na prostą AB. Wykaż, że <)ACD = <)BCO.
29 kwi 19:50
Adamm: mam sposób bez nierówności Jensena
ale z funkcjami 2 zmiennych i ich ekstremami
29 kwi 20:01
Mariusz:
| tg x | |
| +cos2x−sin2x=0 |
| √3+tg x | |
| tg x | | cos2x−sin2x | |
| + |
| =0 |
| √3+tg x | | cos2x+sin2x | |
| tg x | | 1−tg2x | |
| + |
| =0 |
| √3+tg x | | 1+tg2x | |
| tgx(1+tg2x)+(√3+tg x)(1−tg2x) | |
| =0 |
| (√3+tg x)(1+tg2x) | |
tg x(1+tg
2x)+(
√3+tg x)(1−tg
2x)=0
tg
3x+tg x+
√3−
√3tg
2x+tg x−tg
3x=0
−
√3tg
2x+2tg x+
√3=0
3tg
2x−2
√3tg x−3=0
| | π | | π | |
x= |
| +kπ ⋁ x=− |
| +kπ k∊ℤ |
| | 3 | | 6 | |
29 kwi 20:02
Rafal: Adamm, ważne, że działa

Nie chodzi o to, że szczególnie zależy mi na rozwiązaniu
elementarnym, tylko się po prostu zastanawiam, o czym myśleli twórcy, dając takie zadanie.
Przecież nie każdy zna takie metody.
29 kwi 20:07
Adamm: Rafal, a jakie jest rozwiązanie z nierównością Jensena?
29 kwi 20:14
Rafal: P=2r2sinαsinβsinγ
szacujemy iloczyn z góry za pomocą nierówności między średnimi
stosujemy nierówność Jensena
gotowe
29 kwi 20:17
29 kwi 20:22
Adamm:
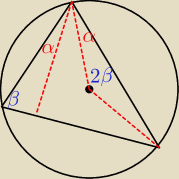
myślę że zadanie dosyć proste
29 kwi 21:10
Adamm:
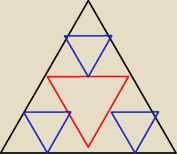
nie mam żadnych zadań, ale jedno wymyśliłem
nie jest zbyt trudne
mamy trójkąt równoboczny o boku a
łączymy środki jego boków i wycinamy z niego trójkąt równoboczny
robimy tak samo z mniejszymi trójkątami itd.
oblicz pole fraktalu powstałego w ten sposób (trójkąta Sierpińskiego)
rysunek trochę słaby, ale pewnie rozumiecie o co chodzi
29 kwi 21:22
matura 2017:
Rozwiąż równanie:
(x+2)(x+3)(x+8)(x+12)=4x2
29 kwi 22:35
Adamm: (x2+11x+24)(x2+14x+24)=4x2
(x2+12,5x+24−1,5x)(x2+12,5x+24+1,5x)=4x2
itd.
29 kwi 22:41
matura 2017: 
29 kwi 22:42
PanTrojkat: Dlaczego akurat 12,5x?
I co by było dalej?
29 kwi 23:09
Adamm: (a−b)(a+b)=a2−b2
29 kwi 23:14
Adamm: dlaczego 12,5x?
bo pasuje
29 kwi 23:17
PanTrojkat: omg, piękne!
29 kwi 23:22
relaa:
Wykazać, że ab(a4 − b4) jest podzielne przez 30.
29 kwi 23:27
Adamm: z małego tw. Fermata
a5b−ab5≡0 mod 5
a5b−ab5≡0 mod 2
a5b−ab5≡0 mod 3
zatem liczba ta jest podzielna przez 5*3*2=30
29 kwi 23:42
relaa:
Bez kongruencji masz pomysł?
29 kwi 23:45
relaa:
Jeszcze jedno dam i idę.
Znaleźć wszystkie n ∊ N dla których wielomian W(x) = (x
3 − 5x + 1)
n + (x
3 − 3x − 1)
n daje
| | 2 | |
przy dzieleniu przez (x − 2) resztę |
| tg(20o)tg(40o)tg(80o). |
| | √3 | |
29 kwi 23:46
Rafal: relaa, chodzi o rozpisanie tg(60−20) i tg(60+20) i skorzystanie ze wzoru
| | 3−tg2(x) | |
tg(3x)=tg(x) |
| , czy też może jest tu jakaś "furtka"?  |
| | 1−3tg2(x) | |
30 kwi 11:34
 maturzystow
maturzystow

 Co do rozwiązań, to może lepiej będzie podawać jedynie pomysły, żeby każdy mógł je zrobić
samodzielnie.
Tak więc:
1) jeśli f(x)=x, to f(f(x))=f(x)=x − w ten sposób znajdujemy dwa pierwiastki, potem wymnażamy
wszystko, dzielimy itd.
2) wzory Viete'a dla wielomianu stopnia trzeciego
3) n rzutów, w pierwszych n−1 za każdym razem możemy dostać 5 wyników, prawdopodobieństwo, że 5
Co do rozwiązań, to może lepiej będzie podawać jedynie pomysły, żeby każdy mógł je zrobić
samodzielnie.
Tak więc:
1) jeśli f(x)=x, to f(f(x))=f(x)=x − w ten sposób znajdujemy dwa pierwiastki, potem wymnażamy
wszystko, dzielimy itd.
2) wzory Viete'a dla wielomianu stopnia trzeciego
3) n rzutów, w pierwszych n−1 za każdym razem możemy dostać 5 wyników, prawdopodobieństwo, że 5





 Najpierw ładne przekształcenia i założenia!
Myślcie dalej..........................
Najpierw ładne przekształcenia i założenia!
Myślcie dalej.......................... 

 Myślcie dalej............
Myślcie dalej............



 Równanie :
Równanie :

 Aby łańcuszek nie stanął:
Punkt O jest środkiem okręgu opisanego na trójkącie ostrokątnym ABC. Punkt D jest rzutem
prostokątnym punktu C na prostą AB. Wykaż, że <)ACD = <)BCO.
Aby łańcuszek nie stanął:
Punkt O jest środkiem okręgu opisanego na trójkącie ostrokątnym ABC. Punkt D jest rzutem
prostokątnym punktu C na prostą AB. Wykaż, że <)ACD = <)BCO.
 Nie chodzi o to, że szczególnie zależy mi na rozwiązaniu
elementarnym, tylko się po prostu zastanawiam, o czym myśleli twórcy, dając takie zadanie.
Przecież nie każdy zna takie metody.
Nie chodzi o to, że szczególnie zależy mi na rozwiązaniu
elementarnym, tylko się po prostu zastanawiam, o czym myśleli twórcy, dając takie zadanie.
Przecież nie każdy zna takie metody.
 myślę że zadanie dosyć proste
myślę że zadanie dosyć proste
 nie mam żadnych zadań, ale jedno wymyśliłem
nie jest zbyt trudne
mamy trójkąt równoboczny o boku a
łączymy środki jego boków i wycinamy z niego trójkąt równoboczny
robimy tak samo z mniejszymi trójkątami itd.
oblicz pole fraktalu powstałego w ten sposób (trójkąta Sierpińskiego)
rysunek trochę słaby, ale pewnie rozumiecie o co chodzi
nie mam żadnych zadań, ale jedno wymyśliłem
nie jest zbyt trudne
mamy trójkąt równoboczny o boku a
łączymy środki jego boków i wycinamy z niego trójkąt równoboczny
robimy tak samo z mniejszymi trójkątami itd.
oblicz pole fraktalu powstałego w ten sposób (trójkąta Sierpińskiego)
rysunek trochę słaby, ale pewnie rozumiecie o co chodzi

