zastosownia wyrażen wymiernych
piotrekk: Paweł przeczytał książkę liczącą 600 stron.Gdyby czytał dziennie średnio o 5 stron więcej,
lektura zajęłabymu 6 dni mniej. Ile dni czytał ę książkę?Ile średnio stron czytał dziennie?
9 gru 20:40
9 gru 20:41
9 gru 20:42
9 gru 20:43
9 gru 20:45
Eta:
Myślę,że wystarczy
9 gru 20:46
bezendu:
x−ilość stron
y−dni
(x+5)(y−6)=600
−3600+5y
2−30y=0
5y
2−30y−3600=0 /5
y
2−6y−720=0
Δ=2916
√Δ=54
x=20
Odp.Czytał 30 dni po 20 stron dziennie
9 gru 20:47
Eta:
9 gru 20:47
bezendu:
Jednak nie wystarczyło
9 gru 20:47
Eta:
Znów gotowiec !
9 gru 20:48
Eta:
Wkurzyłeś mnie ......
9 gru 20:49
bezendu: Nie gotowiec ! Zadanie maturalne za 5 punktów zawsze jest warte rozwiązania...
9 gru 20:49
bezendu:
Czemu ?
9 gru 20:49
Piotr 10: bezendu nie ma co robić najprawdopodobniej
9 gru 20:49
bezendu: A potem na maturze zadanko z ojcem i synem
9 gru 20:52
Eta:
Dla
bezendu ( za karę
Wykaż,że jeżeli w trapez równoramienny da się wpisać okrąg,
to pole trapezu równe jest iloczynowi średniej geometrycznej i średniej arytmetycznej
długości jego podstaw.
9 gru 20:52
ICSP: Eta ja mogę dać karne zadanie dla
bezendu
9 gru 20:54
Piotr 10: ICSP mi możesz dać jedno zadanko
9 gru 20:55
bezendu:
ICSP dziękuję ale nie
9 gru 20:55
Eta:
Jasne,że możesz
9 gru 20:56
ICSP: Jedno z moich ulubionych
Dowieść, że jeśli a,b, ∊ Z oraz 2b
2 + 3 jest liczbą
pierwszą, to liczba U{a
2 − 2}{2b
2 +
3} nie jest całkowita.
Chyba z 30 min mi kiedyś zajęło
Da się zrobić w 2
Dostałem je kiedyś od
Vax'a
9 gru 21:01
ICSP: i to jest zadanie dla
bezendu
9 gru 21:01
bezendu:
jeszcze raz zrobię rysunek bo oznaczenia się nie zgadzają
9 gru 21:04
bezendu:
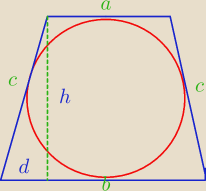
a+b=2c z warunków zadania
h
2=c
2−d
2
| | a2+2ab+b2 | | a2−2ab+b2 | |
h2= |
| −( |
| ) /4 |
| | 4 | | 4 | |
4h
2=a
2+2ab+b
2−(a
2−2ab+b
2)
4h
2=a
2+2ab+b
2−a
2+2ab−b
2
4h
2=4ab /4
h
2=ab /
√
h=
√ab
9 gru 21:08
5-latek: no chyba zartujecie ze to jest zadanie maturalne za 5 punktow
9 gru 21:09
bezendu:
jeśli jest liczbą pierwszą to ma dwa dzielniki. ale co dalej ?
9 gru 21:10
Eta:
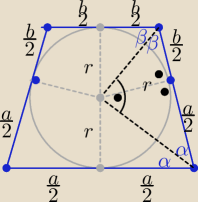
| | ab | | 1 | |
r2= |
| ⇒ r= |
| √ab , h= 2r = √ab |
| | 4 | | 2 | |
c.n.u
9 gru 21:13
bezendu:
5−latek takie zadania zawsze są na podstawowej maturze. Przejrzy sobie arkusze z ubiegłych lat
to się przekonasz jeśli mi nie ufasz
9 gru 21:14
bezendu:
w moim rozwiązaniu brakuje tylko pola
9 gru 21:15
9 gru 21:16
Eta:
bo brakuje P=..
9 gru 21:17
5-latek: bezendu to nie oto chodzi czy ja CI nie ufam .
CHodzi o to z etak proste zadanie jest tak wysoko punktowane . No ale czemu ja sie wlasciwie
dziwie
9 gru 21:19
bezendu:
| | a+b | |
Napisałem przecież, że P= |
| *√ab |
| | 2 | |
h=
√ab
9 gru 21:19
bezendu:
No dobra to może kapkę trudniejsze są...
9 gru 21:19
Eta:
21:16 ja tu P nie widzę ?
9 gru 21:20
bezendu:
Etam zapomniałem dopisać. Proszę usuń post z 21:02 bo tam niezbyt ten rysunek
wyszedł
9 gru 21:22
zombi: | | a2−2 | |
ICSP, mówisz o tym |
| ? Powiedz mi tylko czy jest tak łatwe jak mi się wydaje |
| | 2b2+3 | |
XD. tzn. czy uargumentowanie tego jest takie proste.
9 gru 21:27
ICSP: Kto wie
Dwie linijki : D
9 gru 21:28
zombi: Zastanawiam się jak to sprytnie upakować : D jak nie będę potrafił do 22 max to proszę o
rozwiązanie
9 gru 21:33
ICSP: Ja chce zobaczyć jak to
Vax zrobi
Mam swoje rozwiązanie, ale może da się inaczej
9 gru 21:37
zombi: ICSP pokaż swoje rozwiązanie, bo chce sprawdzić czy byłem chociaż blisko. ; (
9 gru 22:10
ICSP: Wystarczy pokazać, że 2 jest nieresztą kwadratową modulo 2b
2 + 3
Istotnie :
Wystarczy pokazać że 2b
2 + 3 ≡ ± 3 mod 8
Owszem
Niech b = 2k Wtedy :
2b
2 + 3 = 8k + 3 ≡ 3 mod 8
Niech b = 2k + 1 Wtedy :
2b
2 + 3 = 2(4k
2 + 4k + 1) + 3 = 8(k
2 + k) + 5 ≡ 5 ≡ −3 mod 8
c.k.d.
10 gru 12:23
