zadania - planimetria Eta: planimetria ... zadania dla chętnych ... przyszłych maturzystów Zadania pochodzą ze zbioru zadań z r.1966 zad.1/ W równoległoboku o kącie ostrym 60^o wyznaczyć stosunek długości boków

	19
wiedząc,że stosunek kwadratów długości przekątnych jest równy
	7

zad.2/ W trójkącie równoramiennym o podstawie 4 i wysokości 6 , na ramieniu jako na średnicy zakreślono półkole. Punkty przecięcia półkola z podstawą i ramieniem połączono odcinkami. Wyznaczyć pole czworokąta wpisanego w ten okrąg zad.3/ Odcinek stycznej zewnętrznej do dwóch okręgów o promieniach 5 cm i 2 cm jest 1,5 razy dłuższy od odcinka stycznej wewnętrznej . Wyznaczyć odległość między środkami tych okręgów. zad.4/W trójkąt prostokątny wpisano półokrąg tak,że jego średnica leży na przeciwprostokątnej ,a jego środek dzieli przeciwprostokątną na odcinki o długościach 15 cm i 20 cm Wyznaczyć długość łuku półokręgu zawartego miedzy punktami styczności z przyprostokątnymi.

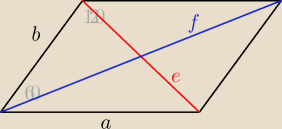
Saizou : f>e i a>b f²=a²+b²−2ab*cos120=a²+b²+ab e²=a²+b²−2ab*cos60=a²+b²−ab

a2+b2+ab		19
	=
a2+b2−ab		7

7a²+7b²−7ab=19a²+19b²−19ab 12a²−26ab+12b²=0

	a
6a2−13ab+6b2=0 :b2		=t t>0
	b

6t²−13t+6=0 Δ=25 √Δ=5

	13−5		8		2
t1=		=		=		sprzeczność bo a>b
	12		12		3

	13+5		18		3
t2=		=		=
	12		12		2

	a		3		b		2
zatem stosunek		=		, a		=
	b		2		a		3

Godzio: W końcu doczekałem się słowa "dla chętnych"

Eta: Witaj Godzio ......... "dla chętnych ...... przyszłych maturzystów"

Eta: zad.1 zaliczone @Saizou ....czekam wciąż na .......rozwiązanie zadania (wiesz którego?

Saizou : a wiem, wiem, tylko tak jakoś mi się nie chce ostatnimi czasy

Eta: Ok ( mam fajny sposób na rozwiązanie tego zadania .... ale jeszcze poczekam do (maja

Godzio:

15		r
	=		/2
20		√202 − r2

9		r2
	=
16		400 − r2

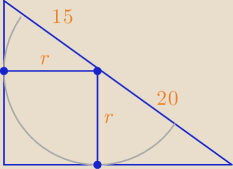
400 * 9 − 9r² = 16r²

	400 * 9		20 * 3
r2 =		⇒ r =		= 12
	25		5

	1
L =		* 2π * 12 = 6π
	4

Godzio: Za późno przeczytałem post

Eta:

Mark: ja mature na 100% zdałem, to chyba dla mnie nie ma szans

Dominik: w sumie juz dawalem tutaj zadanko, ale nikt nie rozwiazal. rozwazmy okregi O₁ i O₂ o odpowiednio srodkach w punktach S₁ i S₂ oraz promieniach dlugosci r₁ i r₂. nalezy wykazac, ze okregi sa rozlaczne zewnetrznie, gdy r₁ + r₂ > |S₁S₂|

gordon122: masakra jakie trudne a muszę rozszerzenie zdawać

Eta: Jedz dużo

bezendu: @gordon122 pierwszy raz Cię tu widzę

Eta: Ja też Witamy gordona w klubie maturzystów("rozszerzonych"

Saizou : Eto czy zadanie nr. 2 ma poprawną treść? Bo wychodzi mi sprzeczność

Saizou : a no już wiem gdzie mam błąd

bezendu: Eta skąd Ty masz tyle

Eta:

Eta: Z sadu , rosną na wierzbie

bezendu: Bardzo dużo masz tych wierzb ( Będziesz jutro ? mam kilka zadań z planimetrii oczywiście podstawa )

Eta: Będę, ale dopiero po południu

gordon122: hehe też witam was xD mam nadzieję że z tą stroną naucze się do matmy roz bo bardzo mi zależy żeby dobrze wypaść

bezendu: A w której klasie jesteś ?

gordon122: teraz w 4

bezendu: to tak jak ja

gordon122: bo chodzi o to że chce isc na inżynierię środowiska lub ochronę środowiska i dowiedziałem się że muszę zdawać rozszerzoną matme i biologię ( jak zdam roz biologie to beda troche większe szanse) ale bardziej mi na tej matmie zależy i wgl jak się przygotować i od kiedy już zacząć bo to będzie dużo z tym roboty xD

bezendu: robić zadania Dużo zadań, najlepiej od teraz

gordon122: chciałbym już od jutra zaczynać ale od totalnej podstawy xD bo o to chodzi że chce coś rozumiec bardzo dobrze, ja nie toleruje korków czy czegoś ja wole sam do czegoś dojść wystarczy jakiś filmk albo dobrze wytłumaczone na stronie

bezendu: to tu masz bardzo dobrze wytłumaczone

gordon122: a korzystasz jeszcze z czegoś oprócz tej strony ?

bezendu: http://www.zadania.info/

gordon122: masz tam wykupiony pakiet ?

bezendu: nie

gordon122: ja korzystam z 2 fajnych serwisów zdawali tam nawet ci "humanisci" ktorzy sie uczyli z tych serwisów na 80% ale nie wiem czy można podawać tutaj xd

bezendu: można

gordon122: www.matemaks.pl www.kurs−maturalny−warszawa.pl ale lepiej na kanale yt : http://www.youtube.com/user/MrCiupi bo jest o wiele wiecej filmików też korzystałem z e−zadania i naszanauka.pl ale bardziej mi te 2 przypadły do gustu

gordon122: te 2 czyli matemaks i mr ciupi xD

bezendu: mr.cupi też oglądałem ''chciałbym już od jutra zaczynać ale od totalnej podstawy '' zobacz godzinę i zaczynaj

gordon122: hahaha w nocy xD ?

Dominik: najlepiej to byloby sie zaopatrzyc w jakis solidny zbior zadan. od siebie moge polecic zbiory pana kielbasy.

gordon122: a jeśli wykupie sobie abonament za 20 zł na zadania.info to wystarczy ? czy jeszcze kupić zbiór a. kiełbasa ?

bezendu: Dominik Ty kiedyś wstawiałeś link do jakieś oficyny ? Masz może jeszcze gdzieś to ?

Dominik: gordon, abonamentu tam nie kupuj, choc strone polecam. kup zbiory pana andrzeja i rozwiazuj zadania po kolei. nie omijaj nawet pozornie trudnych, bo do matury kupa czasu, a w razie trudnosci pisz tutaj na forum. nie znam zadnej z podanych ciebie stron, a mature w tym roku napisalem calkiem dobrze. bezendu, przerobilem te arkusze http://www.pazdro.com.pl/liceum_i_technikum/matematyka-1-2-3-4-5-6-7-8-9-10-11-12-13-14-15-16-17-18-19-20-21-22-23-24-25-26-27-28-29 przy czym niejednokrotnie spotkalem sie z opinia, ze sa to najtrudniejsze arkusze obecne na rynku. dlatego warto je zrobic juz jako doszlifowanie umiejetnosci.

gordon122: a jak kupić ten zbiór pana andrzeja to 2 cz na podst najpierw potem 2 na roz ?

Dominik: jesli chcesz pisac rozszerzenie to tylko poziom rozszerzony. znajduje sie tam czesc zadan z poziomu podstawowego.

gordon122: bo o to chodzi że też muszę bardzo podszlifować podstawę a potem rozszerzenie bo w szkole to wgl nas nic nie uczą a muszę sam się wszystkiego uczyć, teraz sam nie wiem

Dominik: uczylem sie sam, w szkole co semestr mialem zagrozenie z matematyki (wlacznie z trzecia klasa), a mature napisalem na 98%. da sie? da.

gordon122: kurde to widocznie mam to samo co ty to od czego najpierw zacząć ?

Saizou : no i wyszło na to że tylko ja nic nie robię do matury a bezendu przypomnij mi się jutro o skanach zadań, bo ja zapomnę

Dominik: od polubienia matematyki

gordon122: no a co dalej ?

Dominik: Saizou, zerknij na zadanko z 20:50, bo az przykro mi sie robi, ze nikt nie chce go tknac.

Dominik: gordon, jutro jedziesz do ksiegarni, kupujesz "kielbase" i trzaskasz zadanka, az zrobisz wszystkie. innej rady nie ma.

gordon122: no ale żeby zrobić zadania to musze umieć to zrobić nie ? xD

Saizou : nie lubię takich dowodów, bo to są oczywiste oczywistości , ale coś pomyślę

Dominik: gdybym umial robic zadania to bym nie przejmowal sie zbiorami zadan tylko balowal ze znajomymi. na szczescie w kielbasie, jak w wiekszosci zbiorow, obecne jest stopniowanie trudnosci. pierwsze zadania sa, doslownie, podobne do "oblicz: 2+2".

Dominik: Saizou, a ja wlasnie takie najbardziej lubie. powinny byc udowodniane na lekcjach, a nie ze sa oczywistymi oczywistosciami, ktorych nawet nauczyciel nie potrafi udowodnic.

Saizou : znaczy się ja jak widzę rysunek to wiem jaki warunki dać

Dominik: podpowiem, ze dowod jest na jedna linijke.

Saizou : tego to się domyśliłem

gordon122: to mam kupić od razu do rozszerzenia ? od razu 2 części ?

gordon122: wlasnie szperam po necie i widze że jest książka od razu podst i roz w jednym xD to jednak kupie

Dominik: tak, rozszerzenie. i jak masz kase to kup od razu dwie czesci, bo zaraz nadejdzie wrzesien is ie maturzysci rzuca na wykupywanie zbiorow. zbiory pana kielbasy sa chyba najpopularniejszymi.

Saizou : ale okręgi są rozłącznie zewnętrznie, gdy lS₁S₂l>r₁+r₂, wiec zadanie nie ma sensu

gordon122: bardzo dzięki za radę

Dominik: Saizou, pomylilem znak. wiesz jak mialo byc. nota bene wrzucam to zadanie po raz drugi i znowu literowka. moze dlatego dotad go nikt nie rozwiazal?

Saizou : nie mam pojęcia jak to ruszyć

Dominik: pokazac?

Saizou : może jakaś podpowiedź?

Dominik: nierownosc trojkata

Saizou : a co ma nierówność trójkąta do okręgów, bo nie wiem

Dominik: wiecej powiedziec nie moge, bo w zasadzie dalbym ci caly dowod. znajdz tam jakis trojkat.

Saizou : nie ogarniam tego, chyba z późna godzina

Dominik: pokazac czy walczysz jutro?

Saizou : pokaż, bo do wtorku zapomnę xd

Godzio: Gadka szmatka, a zadań nie ma

Dominik: najlatwiej nie wprost. zalozmy, ze okregi przecinaja sie w punkcie A. dla trojkata AS₁S₂ nie zachodzi nierownosc r₁ + r₂ > |S₁S₁|, zatem sprzecznosc. QED.

Dominik: co ja plece, rowniez jestem zmeczony. nie powinno byc tam slowa "nie".

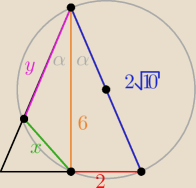
Saizou : czworokąt jest wpisany w okrąg, gdy x+2√10=2+y z tw. cosinusów mamy

	6		3√10
x2=62+y2−2*6*y*cosα oraz cosα=		=
	2√10		10

łącząc te fakty otrzymujemy układ równań x+2√10=2+y

	3√10
x2=36+y2−12y*
	10

no i wychodzi że x=2 i y=2√10, czyli bzdury

Saizou : Eto co sądzisz na temat tego zadanka?

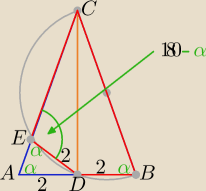
Eta: Poczytaj jaki jest warunek, czworokąta wpisanego w okrąg Z warunku wpisania czworokąta w okrąg ( zaznacz kąty Rozpatrz teraz trójkąty podobne i ich skalę podobieństwa oraz stosunek pól .............. odp: P= 10,8 [j²] Twój zaraz przeanalizuję

Eta: Echhh .... nie ma co "analizować" .... walnąłeś bzdurę !

Saizou : yyyy..... jaką bo się okaże że jestem ślepy

Eta: Warunek wpisania czworokąta w okrąg! jaki jest?

Saizou : sumy przeciwległych boków muszą być równe

Saizou : yyyyyyyyyyyy..........nie to tu przecież są kąty

Eta:

Eta: I jak to będzie na maturze ? co?

Saizou : po prostu siada się na krześle i się piszę

Eta: tylko co się pisze?

Saizou : cyferki i takie tam

Eta: Dawaj następne..... tylko poprawnie rozwiązane, bez "takich tam"

Saizou : teraz muszę lecieć, ale może później coś ruszę

Eta: Ok baw się dobrze

Saizou : "baw się" idę biegać xd

Eta: To też zabawa

^Bartek^: Teraz moja kolej

bezendu: ; Bartek, sinusioidalny, trochę umiem matematykę itp to cały czas jedna i ta sama osoba ?

Eta:

bezendu: https://matematykaszkolna.pl/forum/208023.html post, https://matematykaszkolna.pl/forum/208013.html od dziś unikam jak Ajtek Adasia którego pozdrawiam

Eta: https://matematykaszkolna.pl/forum/208879.html @ Saizou zadanie optymalizacyjne .... na jutro

Theosh: @Eto wymyśl zadania z funkcji kwadratowej pierwsze łatwe dla mnie a resztę trochę trudniejsze.

^Bartek^: '@bezdndu Nie, oprócz" Troche umeim matematyke" ale po co ci to potrzebne? Możesz mnie unikać nie wydaje mi się ,że w czymś mógłbyś mi pomóc.to ci chodzi ,tak? Bo w jaki inny sposób można tutaj unikać ? To nie jest forum do pogawędek tylko do rozwiązywania zadań . nie odpisuj na to i tak juz tuu nie bedee zagladdal

5-latek: Dzien dobry [Eta]] Policzylem zadanie nr 3 i wyszlo mi ze srodki S₁ − S₂ sa odlegle od siebie o 9cm . Dobrze?

5-latek: Nad drugim jeszcze mysle

^Bartek^: [[@5−latek]n] jak to policzyłeś ?

Mila: 5−latek, rysunek tam: https://matematykaszkolna.pl/forum/208929.html 9

Eta: Odp: ...... |O₁O₂|= 9 rys. podała Mila Zadanie pochodzi ze zbiorku z 1966 r. stąd taka terminologia . Pozdrawiam Wszystkich zainteresowanych tym zadaniem

Eta: Rozwiązanie zad.2 podał już Godzio 11 sier 16:31

Eta: Dla Saizou Uzasadnij,że równanie x²⁰¹³+x²⁰¹²−x−2=0 ma dwa pierwiastki rzeczywiste

5-latek: dziekuje Eta i Mila za odpowiedzi . Dopiero teraz bo niedawno wrocilem z pracy . Dobrze ze jutro odpoczne Pozdrawiam rowniez Krystek jesli jest na forum bo dawno jej nie widzialem

Saizou : na pewno ma jeden, bo to wielomian nieparzystego stopnia, czyli ma przynajmniej jedno miejsce zerowe

Eta: czytaj treść ....

Saizou : wiem że chodzi o 2 pierwiastki, ale na razie mam jeden xd

Eta: .........i w tym sęk

Saizou : chyba w drewnie

Eta: O kurczę ma być tak: x²⁰¹⁴ +x²⁰¹³−x −2=0 Przepraszam A w tym co napisałam : uzasadnij,że ma tylko jeden !

Saizou : czyli trzeba uzasadnić że równanie x²⁰¹⁴+x²⁰¹³−x−2=0 ma 2 pierwiastki rzeczywiste

Eta: Tak, podpowiedź: wykresy .........

ZKS: Korzystając z twierdzenie Darboux pokażemy że ten wielomian ma dwa pierwiastki rzeczywiste. W(x) = x²⁰¹⁴ + x²⁰¹³ − x − 2 W(−2) > 0 W(−1) < 0 W(−2) * W(−1) < 0 w przedziale x ∊ (−2 ; −1) znajduje się jeden pierwiastek W(1) < 0 W(2) > 0 W(1) * W(2) > 0 w przedziale x ∊ (1 ; 2) znajduje się drugi pierwiastek.

Eta: Hej ZKS Ma być uzasadnienie na poziomie wiedzy licealnej !

ZKS: Hejka Eta. Hehe a jak by licealista przez przypadek wziął jakąś książkę od kolegi ze studiów i by sobie przeczytał uznała byś?

Eta: Jasne,że tak

Eta: No to dajmy się wykazać licealistom

ZKS: Oczywiście już nic nie będę szkodził.

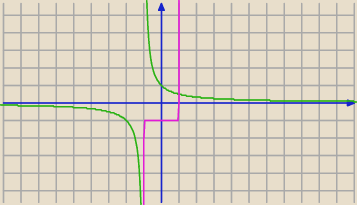
Godzio: Licealnie, czyli wykresik Po małym przekształceniu : (x = −1 nie jest rozwiązaniem)

	1
x2013 − 1 =
	x + 1

5-latek: CzescEta . Rozwiazalem zadanie nr 2 i wynik mi wyszedl taki jaki podalas w swoim poscie z 12sierpnia z godz 18.21 czyli 10,8cm² Wzorowalem sie Twoim rysunkiem z tego postu P_CEDB=P_ABC−P_EAD

	1
PABC=		*AB*CD=12cm2
	2

Trojkat CAD jest podobny do trojkata EAD P_CAD=6cm

	AE
Teraz zapisalem zeU{PEAD{6}=
	AC

AC=√2²+6²=√40=2√10 Teraz ulozylem nastepna proporcje zeby wyliczc AE. Zapisalem ze AE*AC=AD*AB z tego wyliczylem AE Pole trojkata EAD=1,2cm kw. Pole czworokataCEDB=10,8 cmkw. Pytanie . Dobrze jest. Dziekuje za odpowiedz

pigor: ..., 1) Uzasadnij, że równanie x²⁰¹³+x²⁰¹²−x−2=0 ma 1 pierwiastek rzeczywisty. 2) Uzasadnij, że równanie x²⁰¹⁴+x²⁰¹³−x−2=0 ma dwa pierwiastki rzeczywiste. −−−−−−−−−−−−−−−−−−−−−−−−− ad.1)

	x+2
x2013+x2012−x−2=0 ⇔ x2012(x+1)= x+2 ⇒ x2012=		i x≠−1 ⇔
	x+1

	1
⇔ (x1006)2 = 1+		i x≠ −1 − 1 punkt przecięcia wykresów lewek i prawej strony
	x+1

ad.2)

	1
(x671)3 = 1+		i x≠ −1 − 2 punkty przecięcia wykresów . ...
	x+1

Eta: pigor też będziesz zdawać maturę?

5-latek: Eta zobacz na moj post z 18.04. Czy dobrze ?

bezendu: Eta pamiętasz to zadanie: W trójkąt prostokątny wpisano półokrąg tak,że jego średnica leży na przeciwprostokątnej ,a jego środek dzieli przeciwprostokątną na odcinki o długościach 15 cm i 20 cm Wyznaczyć długość łuku półokręgu zawartego miedzy punktami styczności z przyprostokątnymi. czy prawidłowa odpowiedź to L=6π

ZK: Tak. Prawidlowa odpowiedz to L=6π cm.