Zadania atE: Zadania tylko..dla bezendu typu "wykaż" zad1/ Wykaż,że jeżeli środkowa i wysokość poprowadzona z jednego wierzchołka trójkąta dzielą kąt przy tym wierzchołku na trzy równe części, to trójkąt jest prostokątny zad2/ Wykaż,że jeżeli α,β,γ są kątami wewnętrznymi trójkąta i sin²α= sin²β+sin²(α+β) to trójkąt jest prostokątny

bezendu: znowu twierdzenie sinusów

atE:

	1
zad3/ Wykaż,że : cos105o*cos75o =		(√3−2)
	4

	a		b		c
zad4/ Wykaż,że jeżeli liczby a,b,c>0 i		+		+		=1
	b+c		a+c		a+b

	a2		b2		c2
to:		+		+		=0
	b+c		a+c		a+b

atE: Masz podać rozwiązania! .... a nie pisać "znowu"....

use: wykaż że w dowolnym trojkacie prawdziwa jest nierownosc :

√3(a+b+c)
	>√a2+b2+c2 gdzie a,b,c oznaczaja dlugosci bokow trojkata
2

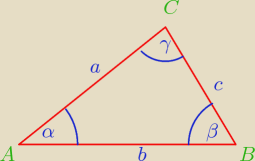
bezendu: Zadanie 2

	c
sinα=
	2r

	a
sinβ=
	2r

	b
sinγ=
	2r

c2		a2		b
	=		+
4r		4r		2r

C.N.D

atE: ....... popraw błędy

Godzio: Kiedysiowe zadanie Etowe zad5/ Udowodnij, że jeżeli długości a,b,c boków trójkąta spełniają warunek:

1		1		3
	+		=
a + b		b + c		a + b + c

to jeden z kątów ma miarę 60^o

atE: Hej Godzio

Godzio: Witam

bezendu: korekta do 2

	c
sinα=
	2r

	a
sinβ=
	2r

	b
sinγ=
	2r

c2		a2		b2
	=		+
4r2		4r2		4r2

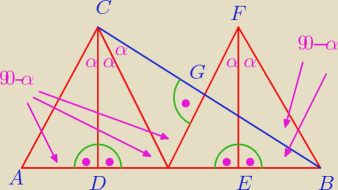
bezendu: zadanie 1

bezendu: można podpowiedź do 3

Godzio: A co to tak szybko się poddajesz, nad niektórymi zadaniami Ety siedziało się kilka godzin !

bezendu: No to nie chcę żadnych wskazówek już

Godzio:

bezendu: zadanie od use

√3(a+b+c)
	>√a2+b2+c2 /2
2

6(ab+ac+bc)>a²+b²+c²

Godzio:

3
	, a nie 6
4

Godzio: A dobra, bo Ty już to trochę uprościłeś, nie było komentarza

Godzio: Ja to widzę tak: a(b + c) + bc > a² + bc b(a + c) + ac > b² + ac c(a + b) + ab > c² + ab Dodaj i działaj dalej, praktycznie już wychodzi.

use: juz prawie jestes w domu bezendu pomysl troche

use: mała podpowiedz; mozesz przeciez skorzystac z tw cosinusow w sumie to juz jest duza podpowiedz^^

bezendu: a+b+c>0 koniec ?

use: nie wiem jak do tego doszedles ja mam tak; 3(2ab+2bc+2ac)>a²+b²+c² z tw cosinusow wynika; a²=b²+c²−2bccosα b²=a²+c²−2accosβ c²=a²+b²−2abcosγ dodajac sronami mam ; a²+b²+c²=2abcosγ+2accosβ+2bccosα≤2ab+2ac+2bc czyli tamta nierownosc jest oczywista

Godzio: To ja dokończę moje, może się przyda a(b + c) + bc > a² + bc b(a + c) + ac > b² + ac c(a + b) + ab > c² + ab (to z nierówności trójkąta) Po dodaniu i uproszczeniu wychodzi: 2(ab + ac + bc) > a² + b² + c² / * 3 6(ab + ac + bc) > 3(a² + b² + c²) > a² + b² + c² Czyli to co otrzymałeś

atE: Hej pomagacze bezendu ma sam myśleć nad poprawnymi rozwiązaniami ... aż do skutku

bezendu:

	√6−√2		√6−√2
cos(90o+150)*cos(90o−15o)=−sin15*sin15=−(		)*		=
	4		4

−√6+√2		√6−√2		−2+√3		1
	*		=		=		(√3−2)
4		4		4		4

C.N.D

bezendu: Eta zobacz zadanie 3

atE: sin15^o = .... podaj dokładnie....skąd ten wynik zad3/ można dokończyć tak: −sin15^o*sin15^o= −sin²15^o cos2α= 1−2sin²α

	cos30o−1		1
cos30o = 1−2sin215o ⇒ −sin215o =		= ....=		(√3−2)
	2		4

bezendu: sin15⁰ wziąłem z tablic→http://www.math.edu.pl/tablice-matematyczne

Saizou : tak szczegółowej tablicy na maturce nie ma witam Wszystkich

atE: Ano właśnie Witaj Saizou

Godzio: Cześć

bezendu: Na maturze może i nie będzie ale to nie moja wina, że akurat na tej stronie są dokładne tablice

atE: To masz nowe wyzwanie Oblicz sin15^o =.......

Saizou : mogę ja, mogę ja

Godzio: Saizou Ty masz obliczyć sin18^o

bezendu: nie nie możesz

atE: Właśnie sin18^o =...

Saizou : a nie cos7^o

atE: Ooooo to też.......... cały czas czekam

Godzio: Jeśli masz na myśli niewykonalność to Cię wyprowadzę z błędu, da się to zrobić, a ja powinienem się uczyć na egzamin, a nie tu siedzieć

Ajtek: Ale się "znęcacie nad bezendu . Witam Eta, Godzio, bezendu, Saizou, use .

Saizou :

	1
jedyny pomysł jaki mam w głowie to sin(		*90o)
	5

atE: Witam Ajtek ( ale gdzie tu jest Eta?

bezendu: sin15⁰=sin(45⁰−30⁰)=sin45⁰*cos30⁰−sin45^o*cos30⁰=

	√2		√3		√2		1		√6−√2
=		*		−		*		=
	2		2		2		2		4

atE:

Godzio:

	sinα = x
Hmm, no to luźny pomysł: sin(5α) = W(sin(α))		W(x)
	=

W(x₀) = 0 ⇒ x₀ = sin18^o = ... (nie gwarantuje zwycięstwa )

bezendu: Cześć Ajtek Eta ja zacząłem robić to z tym cos7⁰ zaraz poszukam

atE:

bezendu: https://matematykaszkolna.pl/forum/205151.html 19:57

Ajtek: Eta widzę, bo mam taką wadę wzroku .

bezendu: Eta rzuć jeszcze okiem na to zadanie 2 (poprawiłem )

ZKS: Niech 18^o = x wtedy sin(5x) = sin(2x + 3x) 5x = 90^o ⇒ 2x = 90^o − 3x sin(2x) = sin(90^o − 3x) sin(2x) = cos(3x) 2sin(x)cos(x) = 4cos³(x) − 3cos(x) / : cos(x) ≠ 0 2sin(x) − 4 + 4sin²(x) + 3 = 0 4sin²(x) + 2sin(x) − 1 = 0 Δ = 1 + 4 √Δ = √5

	−1 − √5		−1 + √5
sin(x) =		< 0 ∨ sin(x) =		> 0.
	4		4

Dobra idę kończyć projekt.

atE: Zad2 do poprawki..........jeżeli chcesz uzyskać max. pkt

Godzio: No, to ja wracam do moich funkcjonałów

atE:

	√5−1
Bardziej elegancki zapis sin(x)=
	4

Pozdrawiam ZKS

atE: No to ja też idę .......... ?

bezendu: jeszcze do poprawki ? chodzi o to że zamiast r² napisać R² ?

bezendu: To ja też idę Dobranoc (resztę zadań jutro)

Godzio: Jak Ty idziesz Przecież Ty masz wolne praktycznie

bezendu:

Ajtek: Godzio, bezendu na randkę leci

Godzio: A to nie zatrzymuję w takim razie

bezendu: Nie na randkę ,ale rano muszę wstać do pracy

Saizou : jak to mówią Arbeit macht frei, miłej nocy

atE: Odkurzam zad. wykaż,że sin47^o+sin61^o−sin11^o−sin25^o= cos7^o korzystam ze wzorów na różnicę sinusów i sumę sinusów: oraz 2*sinα*cosα= sin2α i cos(−α)= cosα L=(sin47^o−sin25^o)+(sin61^o−sin11^o)= 2cos36^o*sin11^o +2cos36^o*sin25^o= =2cos36^o(sin11^o+sin25^o)= 2cos36^o*2sin18^o*cos7^o=

	2sin18o*cos18o *2cos36o*cos7o
=		=P
	cos18o

	sin36o*2cos36o*cos7o		sin72o*cos7o
=		=		= cos7o
	cos18o		cos18o

bo sin72^o= cos18^o Dobranoc Wszystkim

atE: Hej Saizou

bezendu:

atE: Witam też.....bezendu

bezendu: Witam Eta a za jabłuszka dziękuję

atE: Hehe.... jedno było robaczywe

bezendu: Wiedziałem, że tu kryję się jakiś podstęp bo niby czemu dwa,skoro zawsze jest jedno ?

atE: ( całe zdrowiuśkie) .........za prawidłową dedukcję

bezendu: Jakie jest prawdopodobieństwo, że to jest zdrowiutkie ?

atE: P(z)= 5^log₃2−2^log₃5+log₂2=..........

bezendu: 1 % ?

bezendu: dla Ety

ICSP: to może coś ode mnie Równanko : (5−x)^{x3 − 4x2 + x + 6} = 1 z dokładnym opisem rozwiązania.

atE: P(z)= 1 = 100%

bezendu: nie wiem nie miałem prawdopodobieństwa, wyszło 1 więc obstawiałem 1 %

bezendu: ICSP pierwszy raz widzę takie równanie wykładnicze

ICSP: mam jeszcze dwa. Póxniej pokażę Ci fajną metodę rozwiazywania układów równań.

use: ICSP msc zerowe wielomianu i juz jest gitarka bo kazda liczba do potego 0 daje 1

bezendu: x³−4x²+x+6=0 x=4 lub x=2 lub x=3 lub x=−1 ale use tu miało być ze szczególnym opisem rozwiązania

use: a co tu opisywac ?

atE: i 5−x >0

bezendu: ICSP układ z trzema niewiadomymi ? byłbym bardzo wdzięczny

ICSP: źle !

ICSP: nie opisałeś i od razu masz błędy

bezendu: use napisał 21:13 wracam za 15 minut

Eta: @bezendu Równanie trzeciego stopnia ........... ma cztery pierwiastki?

ICSP: Eta x = 6 też pasuje D

Eta: No tak źle wpisałam : 5−x>0 i (5−x)=1

bezendu: 1 −4 1 6 −1 1 −5 6 0 W(x)=(x+1)(x²−5x+6) W(x)=(x+1)(x−2)(x−3) x=−1 x=2 x=3

use: Poleci mi ktos jakis ciekawy film na dzisiejszy wieczor

Dominik: wstret polanskiego.

ICSP: Ksiega ocalenia

Trivial: ICSP, widziałem. Całkiem dobry.

bezendu: https://matematykaszkolna.pl/forum/207386.html ICSP , Eta waszym zdaniem to jest zadanie na poziomie matury rozszerzonej

Mila: "Spaleni słońcem" −poważny "Pożegnania"− romantyczny "Powiększenie".

ICSP: nierówność tak. Trivial. Jeżeli masz metodę rozwiązywania układu równań to co możesz dla niej policzyć ?

5-latek: Jesli wezniesz pod uwage trojkat rownoramienny o katach 36,72,72 i gdzie podstawa tego trojkata jest bok dziesieciokata foremnego wpisanego w okrag a ramieniem promien tego okregu

	x
to mozemy zapisac ze sin18=		:R
	2

Bok dziesieciokata foremnego( wpisanego w okrag o promieniu R ma dlugosc

	R
x=		(√5−1) wylicz z tego ile =sin18
	2

Lub policzyc cos 72 w tym trojkacie i zauwazyc ze cos72=sin18 Bedziesz wtedy nie zielony bezendu a zloty .

bezendu: jeśli chcesz się pośmiać to : ''Dyktator''

Trivial: Admiral General?

Trivial: ICSP, nie rozumiem. Co mogę policzyć dla metody?

bezendu: ICSP a dałbyś radę zrobić to zadanie innym sposobem ? Tam trzeba było skorzystać z granicy,a w informatorze maturalnym granica ciągu nie obowiązuje, więc skoro jest to zadanie maturalne to chyba można jakoś bez tej granicy policzyć ?

ICSP: jaką granicę ? Tam nie ma żadnej granicy

ICSP: https://matematykaszkolna.pl/strona/297.html

Saizou : Witam Wszystkich nieskończonego ciągu geometrycznego też nie ma na maturce

bezendu:

	1
tylko tam jest (		)n
	3

bezendu: Cześć Saizou

ICSP:

	1
a to		nie należy do przedziału (−1;1) ?
	3

bezendu: dobra nie było pytania możesz teraz pokazać to z tym układem równań ?

ICSP: później napiszę

bezendu: ok ale dla 3 niewiadomych ?

Trivial: ICSP, o co chodziło z tą metodą?

ICSP: wydawało ze kiedys porównywałeś jakoś eliminację Gaussa z metodą kolumn jednostkowych

Trivial: aha. ICSP, już po sesji?

ICSP: sesję to ja mam dopiero w styczniu/luitym

Trivial: jak to? nie ma sesji letniej?

ICSP: coś w tym stylu Co tam u Ciebie? Kiedy obrona?

Trivial: Ja już prawie po sesji. Zdecydowanie najcięższa od początku studiów. Obrona nie wiem kiedy, nawet nie wybrałem tematu.

ICSP: Jak to nie wybrałeś tematu ? Masz 7 semestrów licencjatu ?

Trivial: Ja robię inżyniera. 7 semestrów.

ICSP: czyli rozumiem że obronę będziesz miał gdzieś w okolicach lutego/marca ?

Trivial: pewnie początek lutego/koniec stycznia. czemu pytasz?

ICSP: czysta ciekawość

Mila: Pytam, bo mnie bardzo zdenerwowały ostatnie wydarzenia i chciałabym aby wykryto , kto to zrobił.

use: jakie wydarzenia

ICSP: tak więc : rozwiazać układ równań : x + 8y − 5z = 6 3x − 4y + 10z = 9 7x − 6y − 15z = 15 możemy użyć następującego schematu : 1^o Mnożymy drugie równanie przez u , trzecie przez v. Dodajemy równania stronami przy okazji porządkująć wszystko ze względu na x,y,z 2^o Liczymy x zerując współczynniki przy y oraz z 3^o Liczymy y zerując współczynniki przy x oraz z 4^o Liczymy z zerując współczynniki przy x oraz y Na powyższym przykładzie. Wykonuje pkt 1^o : (1 + 3u + 7v)x + (8 − 4u − 6v)y + (−5 + 10u − 15v)z = 6 + 9u + 15v 2^o Zaruje współczynniki przy y oraz przy z 8 − 4u − 6v = 0 −5 + 10u − 15v = 0 stąd :

	5
u =
	4

	1
v =
	2

Podstawiając do równania :

	5		1		5		1
(1 + 3 *		+ 7 *		)x = 6 + 9 *		+ 15 *		⇒ x = 3
	4		2		4		2

3^o Zaruje współczynniki przy z oraz x 1 + 3y + 7v = 0 −5 + 10y − 15v = 0 więc :

	4
u =
	23

	5
v = −
	23

	1
po wstawieniu do równania dostajemy że y =
	2

	1
W identyczny sposób obliczamy z w pkt 4o : z =
	5

x = 3

	1
y =
	2

	1
z =
	5

Pytanie dodatkowe do bardziej doswiadczonych osób Jaka jest nazwa tej metody

ICSP: i masz przykładowy układ równań : x − 2y + 4z = 10 3x + y − 2z = 2 2x + 5y + 6z = −8

use: ICSP jak myslisz mam 86 z matmy dostane sie na jakies lepsze kierunki

ICSP: nie wiem : / Popatrz na ubiegłoroczne progi i wyniki matur. Popatrz na tegoroczne wyniki.

use: no wlasnie sie boe troche o to ze innym tez poszlo w miare obrze ale co tam poki co wazne ze zdalem trzeba teraz premyslec dobrze plan dzialania gdzie by tu uderzyc

ICSP: masz wyniki szkoły i województwa (chyba) w systemie. Sprawdź

use: no wlasnie w gminie jestem nalepszy a w woewodztwie est jakies 800 ludzi lepszych ode mnie \;0

use: gdzies napewno sie zalapie no nic ide spac dobranoc ^^

ICSP: Gratuluje Pytanie tylko czy oliimpijczycy się wliczają.

bezendu: Dziękuje ICSP

bezendu: Mam nadzieję, że ICSP nie obrazisz się ? ale zrobiłem to metodą wyznaczników (Twojego sposobu do końca nie ogarniam ) x−2y+4z=10 3x+y−2z=2 2x+5y+6z=−8 1 −2 4 3 1 −2 W= 2 5 6 1 −2 4 3 1 −2 W=6+60+8−(8−10−36)=112 10 −2 4 2 1 −2 W_x= −8 5 6 10 −2 4 2 1 −2 W_x=60+40−32−(−32−100−24)=224 1 10 4 3 2 −2 W_y= 2 −8 6 1 10 4 3 2 −2 W_y=12−96−40−(16+16+180)=−336 1 −2 10 3 1 2 W_z= 2 5 −8 1 −2 10 3 1 2 W_z=−8+150−8−(20+10+48)=56

	Wx		224
x=		=		=2
	W		112

	Wy		−336
y=		=		=−3
	W		112

	Wz		56		1
z=		=		=
	W		112		2

Trivial: bezendu, dobre wyniki. Teraz rozwiąż to równanie tak jak się to powinno robić − metodą Gaussa (takie ogólniejsze przeciwne współczynniki).

bezendu: ok, chwilkę potrwa wpisywanie tego

bezendu: Trivial ciężko jest znaleźć takie liczby żeby po wymnożeniu została tylko jedna niewiadoma

Trivial: Metoda Gaussa na przykładach: https://matematykaszkolna.pl/forum/101737.html https://matematykaszkolna.pl/forum/194078.html

bezendu: Dzięki, przeanalizuje

Godzio: bezendu wcześniejsze zadania rozwiązane już ?

Saizou : coś takiego x − 2y + 4z = 10 3x + y − 2z = 2 2x + 5y + 6z = −8 1 −2 4 l 10 3 1 −2 l 2 odejmuje w₂−3w₁ oraz w₃−2w₁ 2 5 6 l −8 1 −2 4 l 10 0 7 −14 l −28 dzielę w₂ przez 7 0 9 −2 l −12 1 −2 4 l 10 0 1 −2 l −4 dodaję w₁+2w₂ i odejmuję w₃−9w₂ 0 9 −2 l −12 1 0 0 l 2 0 1 −2 l−4 0 0 16 l−4 dzielę w₃ przez 16 1 0 0 l 2 0 1 −2 l−4 dodaję 2w₃+w₂

	1
0 0 1 l−
	4

1 0 0 l 2

	9
0 1 0 l −
	2

	1
0 0 1 l −
	4

x=2

	9
y=−
	2

	1
z=−
	4

Mila: (1) x−2y+4z=10 (2) 3x+y−2z=2 /*2 (3) 2x+5y+6z=−8 (4) x−2y+4z=10 (5) 6x+2y−4z=4 (6) 2x+5y+6z=−8 dodaję stronami (4) i (5) 7x=14⇔x=2 podstawiam do (1) i (2) i (3) 2−2y+4z=10 3*2+y−2z=2 2*2+5y+6z=−8⇔ (7) −2y+4z=8 (8) y−2z=−4 /*3 (9) 5y+6z=−12 −2y+4z=8 3y−6z=−12 5y+6z=−12 dodaję stronami (8) i (9) itd albo metodą podstawiania.

Trivial: Saizou, nie zgodził Ci się wynik. <:

Saizou : no to idę szukać błędu

bezendu: Cześć Godzio, Saizou jeszcze nie ale mam już pomysł na ''kiedysiowe''

Trivial: Saizou, błąd w pierwszym kroku. −8 − 2*10 = −28, a nie −12.

Saizou : 1 −2 4 l 10 3 1 −2 l 2 odejmuje w2−3w1 oraz w3−2w1 2 5 6 l −8 1 −2 4 l 10 0 7 −14 l −28 dzielę w2 przez 7 0 9 −2 l −28 1 −2 4 l 10 0 1 −2 l −4 dodaję w1+2w2 i odejmuję w3−9w2 0 9 −2 l −28 1 0 0 l 2 0 1 −2 l−4 0 0 16 l 8 dzielę w3 przez 16 1 0 0 l 2 0 1 −2 l−4

	1
0 0 1 l
	2

1 0 0 l 2 0 1 0 l−3

	1
0 0 1 l
	2

x=2 y=−3

	1
z=
	2

Saizou : właśnie zauważyłem i poprawiałem

Trivial: Teraz się wynik zgadza.

Saizou : brawa dla mnie udało mi się

Trivial: Pierwszy Gauss w życiu?

Saizou : tak

Trivial: Chcesz jeszcze jednego? Taki przykład: Znajdź wszystkie rozwiązania układu: x + y + 2z = 0 2y + z = 0 x + 3y + 3z = 0 Rozwiązanie (c jest dowolną liczbą).

	3
x = −		*c
	2

	1
y = −		*c
	2

z = c

Godzio: Będę czekać na "kiedysiowe"

Saizou : 1 1 2 l 0 0 2 1 l 0 1 3 3 l 0 1 1 2 l 0 0 2 1 l 0 0 2 1 l 0 zauważam że w₂=w₃, zatem mogę skreślić jeden wers 1 1 2 l 0 0 2 1 l 0 i teraz nie wiem co dalej

Trivial: Eliminuj do postaci 1 0 ... 0 1 ... Potem powróć do zapisu równań ze zmiennymi x,y,z i zobacz co wyjdzie. PS: Zer po prawej nie musisz pisać, bo i tak zawsze będą zerami.

Saizou : 1 1 2 ← sto dwanaście co się stało 0 2 1 1 1 2

	1
0 1
	2

	3
1 0
	2

	1
0 1
	2

Trivial: OK, teraz powróć do x,y,z. Wybierz z jako parametr c i masz rozwiązanie.

Saizou : no i tu się pojawia problem bo ja laki w tych sprawach

Trivial: Powraca się tak samo jak przechodzi do formy macierzowej, tylko w drugą stronę.

	3
x +		z = 0
	2

	1
y +		z = 0
	2

Saizou : jakie to proste się teraz to wydaje

Trivial: Pozostało wybrać z jako parametr i masz wszystkie rozwiązania.

	3
x = −		c
	2

	1
y = −		c
	2

z = c.

Trivial: No to Saizou, kolejny przykład! x + 2y + z = 12 x + 2y − z = 4 2x − y + z = 5 Rozwiązanie: (x,y,z) = (2,3,4) Uwaga! Pojawi się nowy haczyk, ale będzie prosty do rozwiązania nawet dla początkującego.

Saizou : już się boję

bezendu: ''kiedysiowe''

1		1		3
	+		=
a+b		b+c		a+b+c

	3(ab+ac+b2+bc)
a+b+b+c=		mnożę obustronnie (a+b+c)
	a+b+c

a²+2ab+ac+ab+2b²+bc+ac+2bc+c²=3ab+3ac+3b²+3bc a²+2ab+ac+ab+2b²+bc+ac+2bc+c²−3ab−3ac−3b²−3bc=0 a²−b²+c²−ac=0 −b²=−c²−a²+ac=0 /(−1) b²=c²+a²−ac Godzio sprawdź i ewentualnie popraw ( jak masz wolną chwilę oczywiście )

bezendu: jeszcze jak byś mógł to zobacz 2, poprawiłem ale nie wiem o co chodziło Ecie

ZKS: Zauważamy że jest to wzór Carnota b² = a² + c² − ac

	1
b2 = a2 + c2 − 2 * ac *
	2

b² = a² + c² − 2ac * cos(60^o) tak więc jeden z kątów w tym trójkącie ma 60^o.

bezendu: ZKS moje rozwiązanie nie jest poprawne ?

Saizou : 1 2 1 l 12 1 2 −1 l 4 2 −1 1 l 5 1 2 1 l 12 0 0 −2 l −8 każda liczba y spełnia ten układ 0 −5 −1 l −19

Trivial: Saizou, podałem rozwiązanie. Pogłówkuj trochę.

ZKS: Przecież miałeś udowodnić że w tym trójkącie jeden z kątów jest równy 60^o a ja tam tego udowodnienia nie widzę chyba że ślepnę. Ciągle robisz to samo obliczasz wszystko dobrze a zapominasz zawsze o końcowym udowodnieniu które właśnie dopisałem do Twojego rozwiązania.

bezendu: Dobra, dzięki od teraz już będę pisał wszystko od A do Z

ZKS: I na samym początku mnożysz obustronnie przez (a + b)(b + c) a nie jak napisałeś (a + b + c).

ZKS: A nie przepraszam jest dobrze źle spojrzałem.

Saizou : 1 2 1 l 12 →x+2y+z=12→x=12−6−4→x=2 0 0 −2 l −8 →−2z=−8→z=4 0 −5 −1 l −19 →−5y−z=19→−5y=−19+4→−5y=−15→y=3 ale to za pewne o inną metodę chodzi

Trivial: podpowiedź: zamień wiersze.