zadanka
Saizou :
Eta masz może jakieś zadanka, coby się nie nudzić

31 maj 17:44
ZKS:
Rozwiąż równanie.
| | 252x | | 99 | |
250x + 2*249x + ... + 49*22x + 50*2x = |
| + |
| |
| | (2x − 1)2 | | 4 | |
Takie żebyś się nie nudził.

31 maj 17:48
Ajtek:
Cześć
Saizou, ZKS 
.
ZKS aleś armatę wyciągnął

.
31 maj 18:10
Saizou : na razie sobie wymyśliłem że po lewej stronie jest ciąg o wzorze an=n*251−n
31 maj 18:12
Saizou : Witaj Ajtek i ZKS
31 maj 18:13
ZKS:
Witaj
Ajtuś i
Saizou.

31 maj 18:15
Eta:
zad1/ Wykaż,że jeżeli w trójkącie ABC , |AB|=c, |BC|=a, |AC|=b gdzie: c>b>a>0
o polu równym
4
to |AC|>2
√2
zad 2/ Promień okręgu wpisanego w trójkąt wynosi
r,
a miary kątów wewnętrznych są:
α, β, γ.
Oblicz pole tego trójkąta.
zad 3/ Wysokości trójkąta są równe: h
1, h
2, h
3
Promień okręgu wpisanego w ten trójkąt ma długość
r.
Wykaż,że :
zad 5/ Wykaż,że :
sin47
o+sin61
o−sin11
o−sin25
o =
cos7o
zad 6/ W trójkącie ABC gdzie: |BC|=a, |AC|= b
Środkowe poprowadzone z wierzchołków A i B są do siebie prostopadłe
31 maj 18:15
Ajtek:
Nie tyle ciąg, co jego suma

.
31 maj 18:16
Ajtek:
Witaj
Eta 
.
31 maj 18:16
31 maj 18:17
Eta:
Wszystkich

31 maj 18:17
ZKS:
Witamy i Ciebie
Eta.

31 maj 18:18
Saizou : Eta dzięki wielkie za jabłuszko i witam Ciebie
31 maj 18:19
Eta:
"czarna" ? .......

31 maj 18:19
Ajtek:
Zadanko 5 fajne

.
31 maj 18:22
ZKS:
Tak jakoś wyszło może być cukierkowa
ETA.

31 maj 18:24
Eta:

31 maj 18:32
Saizou :
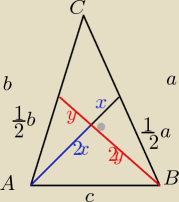
zad 6
c
2=4x
2+4y
2
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
31 maj 18:34
Eta:
zad 7/ Kąty α,β,γ są kątami ostrymi, których suma miar równa jest 90
o
Wykaż,że:
| | α+β | | β+γ | | α+γ | |
cosα+cosβ+cosγ= 4cos |
| *cos |
| *cos |
| |
| | 2 | | 2 | | 2 | |
Idę teraz na herbatkę i .... sernik

31 maj 18:37
bezendu: Zadanie 3 bardzo ładne i przyjemne

31 maj 18:38
Eta:
No to jedno z łatwiejszych zadań , jak dla Ciebie
Saizou 
Zmierz się z ......... trygonometrią

31 maj 18:39
Eta:
@
bezendu 
........ jak tam próbna z rozszerzenia?
31 maj 18:41
bezendu: dopiero jutro będę miał zdjęcia to wstawię, nie zrobiłem jednego zadania oczywiście z
trygonometrii

31 maj 18:42
ZKS:
Kolejne jak coś daje.
(√x)log8(x) ≥ (16x)1/3
31 maj 18:42
Saizou : Eta za chwilę się zmierzę tylko zjem pożywną sałatkę na kolację, aby mieć siły i pomysły

31 maj 18:43
31 maj 18:44
Saizou : sin25=sin(11+14)=sin11*cos14+cos11*sin14
sin61=sin(47+14)=sin47*cos14+cos47*sin14
sin47+sin47*cos14+cos47*sin14 −sin11−sin11*cos14−cos11*sin14 =
sin47(1+cos14)+sin14(cos47−cos11)−sin11(1+cos14)=
(1+cos14)(sin47−sin11)+sin14(cos47−cos11)= i dalej brak pomysłu
31 maj 19:14
Eta:
Zjedz jeszcze jedną sałatkę i......... myśl dalej

31 maj 19:16
Saizou : nie można się zbytnio objadać po 18

31 maj 19:18
ZKS:
To kolejne.

Oblicz wartość wyrażenia
sin(20
o)sin(40
o)sin(60
o)sin(80
o).
31 maj 19:38
Saizou : może troszkę wyhamujcie z zadaniami

31 maj 19:39
Saizou : bezendu jak chcesz to też możesz rozwiązywać
31 maj 19:40
ZKS:
Co tam dla Ciebie takie zadanka.

31 maj 19:41
Saizou : właśnie coś tutaj

w końcu będzie trzeba się za siebie wziąć w wakacje i trochę policzyć

31 maj 19:42
Saizou : niestety muszę teraz was opuścić, ale obiecuję że pomyślę o tych zadanka
31 maj 19:48
bezendu: 
31 maj 19:51
bezendu:
zadanie 5
| cos7o(sin900−180) | | cos70*cos180 | |
| = |
| =cos7 0  |
| cos180 | | cos180 | |
31 maj 19:57
BARTEK: cop kolewiek do zerowej to równa sie jeden
31 maj 20:08
ZKS:
A jak doszedłeś do tej postaci?

31 maj 20:12
bezendu:
| 4cos7o*cos360*sin18o*cos18o | |
| =... i dalej już wiadomo  |
| cos18o | |
31 maj 20:17
BARTEK: a dobrze jest ?
31 maj 20:20
31 maj 20:21
bezendu: nie wiem czy jest dobrze wyszło że niby się zgadza ale trygonometria akurat nie jest mocną
stroną więc może być źle
31 maj 20:22
BARTEK: co zrobilem zle ?
31 maj 20:22
BARTEK: hej ja tam będę dalej się uczył wiec jeśli możecie to zaglądnijcie i dajcie jakaś rade albo
sami zrobcie

31 maj 20:24
bezendu: nie śmieć tu masz swój temat to tam się pytaj...
31 maj 20:24
ZKS:
Lepiej wrzucaj od początku jak robisz bezendu bo znikąd nie wiadomo jak otrzymałeś
tą co teraz napisałeś postać.
31 maj 20:28
Amigo: Saizou, mam kilka fajnych zadanek z trygonometrii, jak chcesz to pisz!
31 maj 20:39
ZKS:
To wrzucaj będą mieli na później.
31 maj 20:47
31 maj 20:54
BARTEK: Sprawdź to ziom!
31 maj 20:55
bezendu: Ziom nie spamuj tutaj

nie widzę żebyś coś tam policzył więc co tam do sprawdzania ?
31 maj 20:56
BARTEK: liczę na kartce ciągle tam Basia trochę policzyła ale ja
akurat tego nie rozumie

31 maj 20:58
Saizou : więc trzeba by wrócić do zadanek

2 cze 16:14
Saizou :
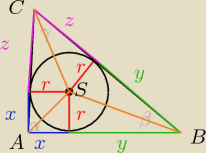
w Δ ABS
w Δ ACS
| | 2x+2y+2z | |
PABC= |
| *r= (x+y+z)r |
| | 2 | |
2 cze 16:34
2 cze 17:35
2 cze 17:35
Eta:
Hej
 zad1, zad 5, zad 7 z 18 maj 18:15 i 18:37
zad1, zad 5, zad 7 z 18 maj 18:15 i 18:37
wiąż czekają na rozwiązania

2 cze 17:41
bezendu:
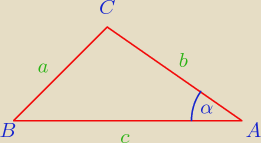
cbsinα=8
cb>8
c
2>cb
c
2>8
c>2
√2
i właśnie tu wychodzi |AB|>2
√2 a nie AC

14 cze 14:45
bezendu: 
14 cze 21:27
Mila:
Bezendu, gdy już się uporasz z tymi zadaniami , to proponuję Ci rozwiązanie ciekawego
zadania, na poziomie klasy || z geometrii, jest tam wskazówka.
Zaraz podam adres.
14 cze 21:46
14 cze 21:47
Mila:
To zadanie też dla Saizou
14 cze 21:51
14 cze 21:57
Mila:
Nie mogę się zorientować, jak to była treść, jeśli to zadanie od Pani Ety, to czekaj
cierpliwie, na pewno Ci sprawdzi..
14 cze 22:04
bezendu: Mila mam jeszcze do Ciebie takie pytanie
Nie mam teraz obecnie zbioru Andrzeja Kiełbasy i robię zestawy powtórzeniowe z Operonu i nie
wiem czy nie lepiej było by robić arkusze maturalne

14 cze 22:15
Mila:
Myślę, że możesz rozwiązywać zestawy Operonu, są dość trudne, zmuszają do myślenia.
Jakie miałaś zbiory zadań do lekcji?
14 cze 22:20
14 cze 22:26
Mila: To dobre materiały.
Rozwiązuj spokojnie, systematycznie i będzie dobrze na maturze i na studiach.
14 cze 22:29
bezendu: Już skończyliśmy tą książkę a nowej do 4 klasy technikum nie mam jeszcze, ale mam za to : Zbiór
zadań z matematyki dla klas I i II szkoły średniej Norbert Dróbko, Karol Szymański

14 cze 22:32
Eta:
Hej
 bezendu
bezendu
| | 1 | |
A tak: P= |
| a*b*sinγ ....... |
| | 2 | |
14 cze 23:18
bezendu: Hey przemalowana Eta a sprawdzisz jeszcze to drugie zadanie link 21:57 ?
14 cze 23:24
kuba : mam pytanko jak obliczyć wysokość w trójkącie równo równoramiennym podstawa 3 boki 10
14 cze 23:25
bezendu: z pitbgorasa
14 cze 23:30
Eta:
bezendu jest ok

14 cze 23:41
bezendu: 
15 cze 00:01
magda: Wiadomo, że cos36=√5+1/4. Wykaż, że a) cos18= √2√5+10/4
16 paź 18:56


 .
ZKS aleś armatę wyciągnął
.
ZKS aleś armatę wyciągnął  .
.

 .
.
 .
.







 .
.


 zad 6
c2=4x2+4y2
zad 6
c2=4x2+4y2


 Zmierz się z ......... trygonometrią
Zmierz się z ......... trygonometrią 
 ........ jak tam próbna z rozszerzenia?
........ jak tam próbna z rozszerzenia?





 Oblicz wartość wyrażenia
sin(20o)sin(40o)sin(60o)sin(80o).
Oblicz wartość wyrażenia
sin(20o)sin(40o)sin(60o)sin(80o).


 w końcu będzie trzeba się za siebie wziąć w wakacje i trochę policzyć
w końcu będzie trzeba się za siebie wziąć w wakacje i trochę policzyć 





 nie widzę żebyś coś tam policzył więc co tam do sprawdzania ?
nie widzę żebyś coś tam policzył więc co tam do sprawdzania ?


 w Δ ABS
w Δ ABS
 http://books.google.pl/books?id=BT27p1XJtBAC&printsec=frontcover&dq=core+mathematical+problems&hl=pl&sa=X&ei=GmarUbztHeO64ATOtoHIAQ&ved=0CDIQ6AEwAA
http://books.google.pl/books?id=BT27p1XJtBAC&printsec=frontcover&dq=core+mathematical+problems&hl=pl&sa=X&ei=GmarUbztHeO64ATOtoHIAQ&ved=0CDIQ6AEwAA
 http://books.google.pl/books?id=BT27p1XJtBAC&printsec=frontcover&dq=core+mathematical+problems&hl=pl&sa=X&ei=GmarUbztHeO64ATOtoHIAQ&ved=0CDIQ6AEwAA
http://books.google.pl/books?id=BT27p1XJtBAC&printsec=frontcover&dq=core+mathematical+problems&hl=pl&sa=X&ei=GmarUbztHeO64ATOtoHIAQ&ved=0CDIQ6AEwAA
 zad1, zad 5, zad 7 z 18 maj 18:15 i 18:37
wiąż czekają na rozwiązania
zad1, zad 5, zad 7 z 18 maj 18:15 i 18:37
wiąż czekają na rozwiązania 






 bezendu
bezendu

