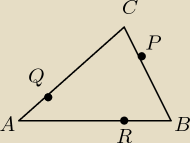
pole trojkata trojkat: Pole trojkata ABC jest rowne 21. oblicz pole trojkata, ktorego boki sa zawarte w prostych: AP, BQ i CR, jesli |RB|=1/3|AB|, |PC|=1/3|BC| oraz |QA|=1/3|CA|

PW:

	1
To jest trudne zadanie. Mogę podpowiedzieć, że pole jest równe		pola trójkąta ABC.
	7

Pisanie tutaj całego dowodu zajęłoby godzinę.

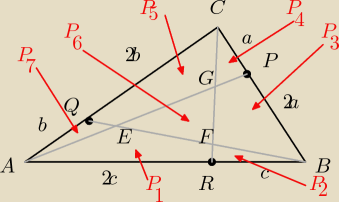Saizou : P_EFG=P₆=? P_ABC=21 nich h₁, h₂, h₃ są wysokościami opuszczonymi odpowiednio z wierzchołków A, B, C

	2c*h3
PACR=		=ch3
	2

	c*h3		1		3
PBCR=		=		ch3 → 2PBCR=PACR → PABC=		PACR
	2		2		2

analogicznie dla pozostałych boków

	3
PABC=		PBCQ
	2

	3
PABC=		PABP
	2

	3
PABC=		PACR
	2

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− +

	3
3PABC=		(PBCQ+PABP+PACR)
	2

2P_ABC=P_BCQ+P_ABP+P_ACR 2P_ABC=P₃+P₄+P₅+P₆+P₁+P₂+P₃+P₆+P₁+P₅+P₆+P₇ 2P₂+2P₄+2P₆+2P₇=P₂+P₄+3P₆+P₇ P₆=P₂+P₄+P₇ a dalej nie a=mam pomysłu

Mila: Niech P_ΔABC=P Saizou, oblicz pole ΔCPG( oznacz np. S), w tym celu poprowadź pomocniczy odcinek GB. P_ΔPGB=2S

	1
PΔBGR=		P−3S
	3

	1
dalej sobie poradzisz ( ma wyjść S=		P}
	21

Bogdan: Eta pozdrawiam

b.: Mila, a co dalej z ΔBGR?

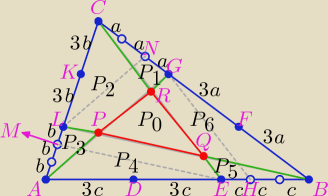Bogdan: Pola: P_ABC = 21, P_PQR = P₀, P_CRG = P₁, P_LPRC = P₂, P_APL = P₃ P_AEQP = P₄, P_EBQ = P₅, P_BGRQ = P₆. P₁ + P₂ + P₃ + P₄ + P₅ + P₆ = 21 − P₀

	1
P1 + P2 + P3 =		*21 = 7
	3

	1
P3 + P4 + P5 =		*21 = 7
	3

	1
P5 + P6 + P1 =		*21 = 7
	3

+ −−−−−−−−−−−−−−−−−−−−−−− P₁ + P₂ + P₃ + P₄ + P₅ + P₆ + (P₁ + P₃ + P₅) = 21 21 − P₀ + (P₁ + P₃ + P₅) = 21 ⇒ P₀ = P₁ + P₃ + P₅ ******************************************************************************************

	1
PEBC =		*21 = 7
	3

HG ∥ EC,

	2		2		4		28
ΔHBG ∼ ΔEBC w skali		, PHBG = PEBC*(		)2 = 7*		=
	3		3		9		9

	2		28		98
PABG =		*21 = 14, PAHG = PABG − PHBG = 14 −		=
	3		9		9

	6c		6
ΔAER ∼ ΔAHG w skali		=		,
	7c		7

	6		98		36
P0+P4 = PAER = PAHG*(		)2 =		*		= 8
	7		9		49

	2
ΔAEC: P2 + P3 + P4 + P0 =		*21 = 14 ⇒ P2 + P3 + 8 = 14 ⇒ P2 + P3 = 6
	3

	1
ΔAGC: P1 + P2 + P3 =		*21 = 7 ⇒ P1 + 6 = 7 ⇒ P1 = 1
	3

******************************************************************************************

	1
PABL =		*21 = 7
	3

ME ∥ LB

	2		2		4		28
ΔAEM ∼ ΔABL w skali		, PAEM = PABL*(		)2 = 7*		=
	3		3		9		9

	2		28		98
PAEC =		*21 = 14, PMEC = PAEC − PAEM = 14 −		=
	3		9		9

	6b		6
ΔLQC ∼ ΔMEC w skali		=		,
	7b		7

	6		98		36
P0 + P2 = PLQC = PMEC*(		)2 =		*		= 8, P2 = P4
	7		9		49

	2
ΔLBC: P1 + P2 + P0 + P6 =		*21 = 14 ⇒ 1 + 8 + P6 = 14 ⇒ P6 = 5
	3

	1
ΔEBC: P1 + P6 + P5 =		*21 = 7 ⇒ 1 + 5 + P5 = 7 ⇒ P5 = 1
	3

*****************************************************************************************

	1
PAGC =		*21 = 7
	3

LN ∥ AG

	2		2		4		28
ΔLNC ∼ ΔAGC w skali		, PLNC = PAGC*(		)2 = 7*		=
	3		3		9		9

	2		28		98
PLBC =		*21 = 14, PLBN = LLBC − PLNC = 14 −		=
	3		9		9

	6a		6
ΔPBG ∼ ΔLBN w skali		=		,
	7a		7

	6		98		36
P0 + P6 = PPBG = PLBN*(		)2 =		*		= 8 ⇒ P0 + 5 = 8
	7		9		49

P₀ = 3 P₂ = P₄ = P₆ = 5 P₁ = P₃ = P₅ = 1

mmk: Witam Bogdanie Myślałam,że jest jakiś bardzo krótki sposób rozwiązania

Bogdan: Dobry wieczór . Może jest krótszy sposób, będę jeszcze próbował znaleźć ładniejsze rozwiązanie.