Geometria analityczna
bezendu:
Proste zadanko:
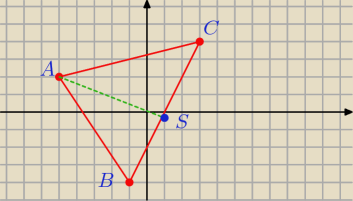
Dany jest trójkąt ABC o wierzchołkach A=(−5,2) B=(−1,−4) C=(3,4). Wyznacz równanie prostej,w
której zawarta jest wysokość poprowadzona z wierzchołka A
środek odcinka BC =(1,0)
prosta przechodząca przez punkty B i C
−a+b=−4 /(−1)
3a+b=4
a−b=4
3a+b=4
4a=8
a=2
b=−2
y=2x−2
prosta prostopadła do prostej y=2x−2
2*a=−1
2a=−1
i przechodząca przez punkt S
I teraz moje pytanie skąd wiadomo, że ta prosta dzieli bok AC na dwie równe części

ten
trójkąt nie jest równoboczny ani równoramienny wiec skąd to wnioskować


10 cze 19:55
Saizou : a czemu przez punkt S? przecież przechodzi ona przez punkt A, który masz dany

10 cze 20:01
bezendu: Dzięki

10 cze 20:05
Eta:
Prosta AS zawiera wysokość ( S nie jest środkiem odcinka AB

jest dowolnym punktem€ BC
zatem jest prostopadła do prostej BC i przechodzi przez A
| | 4+4 | |
wsp. kier aBC= |
| = 2 |
| | 3+1 | |
| | 1 | |
zatem prosta AS: y= − |
| (x−xA)+yA |
| | aBC | |
y=.........
dokończ
10 cze 20:05
Eta:
Miało być :
"S nie jest środkiem odcinka BC"
10 cze 20:07
bezendu: Dziękuje
Eta właśnie coś mi tu nie pasowało tym bardziej że zadanko z podstawy

10 cze 20:07
Saizou : prosta AS, gdzie S jest środkiem odcinka BC jest środkową trójkąta opuszczona z wierzchołka A
10 cze 20:08
bezendu: właśnie to by się wtedy zgadzało bo środkowa dzieli bok na dwie równe części

10 cze 20:09
Eta:
Dla
bezendu  zad1
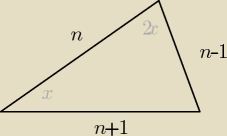
zad1 Długości boków trójkąta są kolejnymi liczbami naturalnymi.
Miara największego kata jest dwukrotnie większa od miary kąta najmniejszego.
Oblicz długości boków tego trójkąta.
zad2 W trójkącie prostokątnym ABC o przeciwprostokątnej AB poprowadzono
prostą KL prostopadłą do przeciwprostokątnej.
Prosta ta przecięła przyprostokątną BC w punkcie K .
Wykaż,że :
|∡KAB| = |∡BCL|
10 cze 20:58
bezendu: Eta jak Ty o mnie dbasz

masz moją dozgonną wdzięczność

10 cze 21:02
Ajtek:
Witam
Eta,
bezendu,
Saizou 
.
Eta pyszne zadanka jak


.
10 cze 21:03
bezendu: Witaj Ajtek
10 cze 21:04
Eta:
Witam
Wszystkich .......
niebieskich i
zielonych 
10 cze 21:05
bezendu:
Zadanie 1
Skoro są kolejnymi liczbami naturalnymi to długości ich boków wyrażają się następująco
n,n+1,n+2
i teraz z twierdzenia sinusów ?
10 cze 21:06
Eta:
zad1 Pamiętaj,że ...nie k
ata

....... tylko k
ąta

10 cze 21:07
Eta:
zad1/
ciepło,
ciepło ,ale jeszcze nie
gorąco 
10 cze 21:08
bezendu:
| n | | n+2 | | n+2 | |
| = |
| = |
| |
| sinα | | sin2α | | 2sinαcosα | |
| | n+2 | |
cosα= |
| dobrze jak do tej pory  czy robić od nowa  |
| | 2n | |
10 cze 21:13
Eta:
Bardzo dobrze

10 cze 21:14
bezendu: Pytam się po te twierdzenia poznałem nie dawno i jeszcze nie jestem pewny tego co piszę

| n | | sinα | |
| = |
|  jak to tej pory ok |
| n+1 | | sincos2α+sin2αcosα | |
10 cze 21:26
Eta:
Teraz z tw, cosinusów:
| | b2+c2−a2 | |
cosα= |
| =........ |
| | 2bc | |
i porównaj te cosinusy
10 cze 21:28
bezendu: | n | | sinα | |
| = |
| |
| n+1 | | sincos2α+2sincos2α | |
| n | | 1 | |
| = |
| i tu się zatrzymałem  |
| n+1 | | 4cosα−1 | |
10 cze 21:31
bezendu: Eta można prosić jeszcze o naprowadzenie

10 cze 21:37
10 cze 21:43
Saizou : mogę też się dołączyć, ale tak na góra 2 zadanka ?
10 cze 21:52
Saizou : jkb to pamiętam o tamtych zadankach

10 cze 21:52
bezendu:
i teraz takie pytanie wyznaczam tu dziedzinę tak jak w każdym równaniu wymiernym

n∊R\{−1}
4n+4=n
2+n
−n
2+3n+4=0
Δ=3
2−4*(−1)*4=25
n=4
n=5
n=6
10 cze 21:53
bezendu: Saizou 
10 cze 21:54
Eta:
Na początku zadania napisać: n€N+
10 cze 21:55
Eta:
Właśnie .... ja pamiętam,że nie dokończyliście rozwiązań poprzednich zadań

10 cze 21:57
bezendu: Założenia no tak miałem je pisać

a to że wyznaczyłem dziedzinę i napisałem takie założenie
jest ok

10 cze 21:57
Eta:
tak

10 cze 21:59
bezendu: dobra ja mykam jutro sprawdzian z analitycznej (a to drugie zadanko rozwiąże jutro ) Dobranoc i
dziękuję za zadanka


10 cze 22:01
Eta:
Powodzenia na sprawdzianie

10 cze 22:02
bezendu: Dziękuje

10 cze 22:03
Saizou :
no i z tw. sinusów n∊N i n>1
(n−1)sin2x=sinx(n+1)
2sinxcosx(n−1)−sinx(n+1)=0
sinx(2cosx(n−1)−(n+1))=0
brak nam cosinusa więc z tw. carnota
(n−1)
2=n
2+(n+1)
2−2n(n+1)*cosx
n
2−2n+1=n
2+n
2+2n+1−2n(n+1)cosx
−n
2−4n=−2n(n+1)cosx
n+4=2(n+1)cosx
| | n+4 | |
sinx(2* |
| (n−1)−(n+1))=0 |
| | 2(n+1) | |
| | n+4 | |
sinx( |
| (n−1)−(n+1))=0 |
| | n+1 | |
sinx=0
(n+4)(n−1)−(n+1)(n+1)=0
(n+4)(n−1)−(n+1)
2=0
n
2+3n−4−n
2−2n−1=0
n=5
zatem te boki to
4,5,6
10 cze 22:06
Eta:


10 cze 22:12
Saizou : Eta mogę poprosić o unikatowe zadanko na dobranoc?
10 cze 22:20
10 cze 22:22
Saizou : ale nie geometria, moja głowa już dzisiaj do czegoś takiego nie jest przystosowana

10 cze 22:23
Saizou : aaaa... zapomniałem o trygonometrii cosinus 7
o 
10 cze 22:24
Eta:
No właśnie .....= cos7
o 
10 cze 22:28
Saizou : nie dzisiaj na pewno nie dzisiaj, może coś innego, niepowtarzalnego, coś z nowego zestawu zadań
10 cze 22:30
Eta:
zad3/ W trapezie równoramiennym ABCD , AB ∥ CD
podstawa AB jest trzy razy dłuższa od podstawy DC.
Wykaż,że przekątne trapezu dzielą środkową EF trapezu
w stosunku 1: 2:1
10 cze 22:52
5-latek : Eta prosze przypomniec tym dwom Panom ze nie rozwiazali jeszcze tamtych zadan o ktore
usilnie prosil
Saizou co mu sie wtedy tak nudzilo

10 cze 23:05
10 cze 23:08
Saizou : Eta zadanko mam zrobione tylko ze w domu napisze, bo jestem na telefonie i nie zbyt
przyjemnie sie pisze
11 cze 13:52
bezendu:
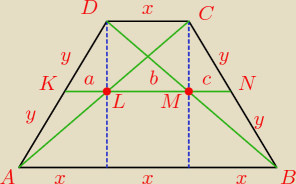
| | 1 | |
ΔAKL∼ΔADL bok bok bok skala podobieństwa k= |
| |
| | 2 | |
b=x
C.K.D
14 cze 14:55
Saizou :
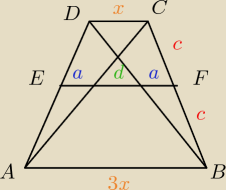
2x=2a+d
2x=2a+x
x=2a
a : d : a
1:2:1
cnu
14 cze 22:15
 Proste zadanko:
Dany jest trójkąt ABC o wierzchołkach A=(−5,2) B=(−1,−4) C=(3,4). Wyznacz równanie prostej,w
której zawarta jest wysokość poprowadzona z wierzchołka A
środek odcinka BC =(1,0)
prosta przechodząca przez punkty B i C
−a+b=−4 /(−1)
3a+b=4
a−b=4
3a+b=4
4a=8
a=2
b=−2
y=2x−2
prosta prostopadła do prostej y=2x−2
2*a=−1
2a=−1
Proste zadanko:
Dany jest trójkąt ABC o wierzchołkach A=(−5,2) B=(−1,−4) C=(3,4). Wyznacz równanie prostej,w
której zawarta jest wysokość poprowadzona z wierzchołka A
środek odcinka BC =(1,0)
prosta przechodząca przez punkty B i C
−a+b=−4 /(−1)
3a+b=4
a−b=4
3a+b=4
4a=8
a=2
b=−2
y=2x−2
prosta prostopadła do prostej y=2x−2
2*a=−1
2a=−1
 ten
trójkąt nie jest równoboczny ani równoramienny wiec skąd to wnioskować
ten
trójkąt nie jest równoboczny ani równoramienny wiec skąd to wnioskować 



 jest dowolnym punktem€ BC
zatem jest prostopadła do prostej BC i przechodzi przez A
jest dowolnym punktem€ BC
zatem jest prostopadła do prostej BC i przechodzi przez A


 zad1 Długości boków trójkąta są kolejnymi liczbami naturalnymi.
Miara największego kata jest dwukrotnie większa od miary kąta najmniejszego.
Oblicz długości boków tego trójkąta.
zad2 W trójkącie prostokątnym ABC o przeciwprostokątnej AB poprowadzono
prostą KL prostopadłą do przeciwprostokątnej.
Prosta ta przecięła przyprostokątną BC w punkcie K .
Wykaż,że :
|∡KAB| = |∡BCL|
zad1 Długości boków trójkąta są kolejnymi liczbami naturalnymi.
Miara największego kata jest dwukrotnie większa od miary kąta najmniejszego.
Oblicz długości boków tego trójkąta.
zad2 W trójkącie prostokątnym ABC o przeciwprostokątnej AB poprowadzono
prostą KL prostopadłą do przeciwprostokątnej.
Prosta ta przecięła przyprostokątną BC w punkcie K .
Wykaż,że :
|∡KAB| = |∡BCL|
 masz moją dozgonną wdzięczność
masz moją dozgonną wdzięczność 
 .
Eta pyszne zadanka jak
.
Eta pyszne zadanka jak 
 .
.

 ....... tylko kąta
....... tylko kąta 

 czy robić od nowa
czy robić od nowa 


 jak to tej pory ok
jak to tej pory ok 


 n∊R\{−1}
4n+4=n2+n
−n2+3n+4=0
Δ=32−4*(−1)*4=25
n∊R\{−1}
4n+4=n2+n
−n2+3n+4=0
Δ=32−4*(−1)*4=25


 a to że wyznaczyłem dziedzinę i napisałem takie założenie
jest ok
a to że wyznaczyłem dziedzinę i napisałem takie założenie
jest ok 





 no i z tw. sinusów n∊N i n>1
no i z tw. sinusów n∊N i n>1








