NAUKA
BARTEK: Kto pouczy się ze mną trygonometrii z uwzględnieniem pól trójkątów? Proszę
Ja będę podawał zadanie i wspólnie albo wy tylko wskażecie jak.
Zad 1
| | 12 | |
W trójkącie prostokątnym cosinus jednego z kątów jest równy |
| ,a promień okręgu |
| | 13 | |
opisanego na tym trójkącie jest równy 13 cm. Oblicz pole tego trójkąta.
31 maj 20:07
Basia:
wskazówka: środek tego okręgu to środek przeciwprostokątnej
31 maj 20:11
BARTEK:
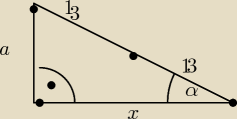
tak.
x=24
a
2=169−144
a=5
P=12*5
P=60 cm
2
W książce jest napisane że powinno być 120 cm2
31 maj 20:19
Basia: błąd w tw.Pitagorasa
a2 = 262 − 242
31 maj 20:21
BARTEK: Dzięki Basiu
a=10
P=120 cm
2
31 maj 20:27
BARTEK: Zad 2.
| | 3 | |
W trójkącie prostokątnym sinus jednego z kątów jest równy |
| . Promień okręgu wpisanego w |
| | 5 | |
ten trójkąt ma długość 7 cm. Oblicz pole tego trójkąta.
ZAPRASZAM
31 maj 20:34
Basia:
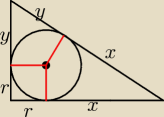
x=a−r
y=b−r
x+y = c
a−r+b−r=c
a+b−c = 2r
stąd masz
a+b−c = 14
drugie równanie z sinusa
trzecie z Pitagorasa
no i układ
31 maj 20:39
BARTEK: nie nie wiem jak to zroibc

31 maj 20:46
BARTEK: MYŚLĘ i myślę i chyba nic już nie wymyśle
31 maj 20:51
Basia:
3c = 5a
3a + 3b + 5a = 42
8a + 3b = 42
a
2 + (14−
83a)
2 = (
53a)
2
dalej licz sam
31 maj 21:03
BARTEK: Basia patrz na to

a=3k, b=4k, c=5k
3k/5k=3/5=sinα
r=7
r=(a+b−c)/2
7=(3k+4k−5k)/2
7=2k/2
7=k
stad a=3*7=21, b=4*7=28, c=5*7=35 najdłuższy bo to przeciwprostokątna więc:
P=1/2*21*28=294 cm²
31 maj 21:05
BARTEK: Skąd u ciebie się wzięło :
| | 5 | |
a+b+ |
| a= 14  |
| | 3 | |
31 maj 21:08
Basia:
pomyłka; minus ma być
a+b−c = 2r
a+b − 53c = 14
31 maj 21:31
BARTEK: no wiedzielem !
31 maj 22:18
BARTEK: juz to zrobilem sam!
31 maj 22:18
BARTEK: Pole równa się 294
31 maj 22:18
BARTEK: Dzięki Basia <3
31 maj 22:19
BARTEK: Zad 3
| | 2 | |
W Trójkącie prostokątnym o polu 12 cm2 tangens jednego z kątów ostrych jest równy |
| . |
| | 3 | |
Wyznacz wysokość poprowadzoną z wierzchołka kąta prostego. Podaj przybliżenie dziesiętne z
dokładnością do 0,1 cm.
ZAPRASZAM!
31 maj 22:26
BARTEK:
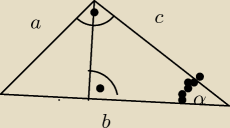
Co dalej ?
31 maj 22:35
ZKS:
| 1 | | 2 | | 2x | |
| ab = 12 ∧ tg(α) = |
| = |
| |
| 2 | | 3 | | 3x | |
2x * 3x = 24
x
2 = 4 ⇒ x = 2
a = 4 ∧ b = 6
c =
√42 + 62 = 2
√13
Teraz podaj przybliżenie swoje.
31 maj 22:35
BARTEK: zrobilem to : Wynik to 3,3 cm
1 cze 00:21
BARTEK: | | 84 | |
W trójkącie prostokątnym o polu 126,5 cm2 cosinus jednego z kątów jest równy |
| . |
| | 85 | |
Oblicz długość boków tego trójkąta.
1 cze 00:23
Basia:
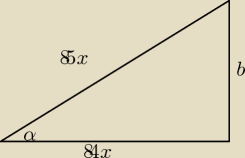
b liczysz z tw.Pitagorasa
b
2 = (85x)
2 − (84x)
2 = x
2(85
2−84
2) = x
2(85−84)(85+84) = 169x
2
b = 13x
P = 84x*13x = 126,5
84*13*x
2 = 126,5
z tego wylicz x
podstaw
a = 84x
b = 13x
c = 85x
i gotowe
1 cze 01:09
Basia: sorry
84*13x
2 = 253
1 cze 01:55
BARTEK:
Dzięki Basia
w mojej szkole robimy innym sposobem chciałbym żebyście sprawdzili gdzie jest błąd proszę.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
| | 84 | | b | | 84 | |
cosα = |
| = |
| ⇒ b= |
| c |
| | 85 | | c | | 85 | |
a
2 = c
2−b
2
−−−−−−−−−−−−−−−−−Teraz próbuję obliczyć c:
| | 1 | | 13 | | 84 | |
136,5= |
| * |
| c* |
| c |
| | 2 | | 85 | | 85 | |
c
2=1972425
c=1404,43049

Powinno być 5,3 cm, 42 cm 42,5 cm
Co zrobiłem źle ?
1 cze 12:16
Nienor: bo w zadaniu pisało 126,5 ma pole, a nie jak ty napisałeś 136,5
1 cze 12:23
Nienor: Choć i tak nie wychodzi liczba wymierna.
1 cze 12:23
BARTEK: Ja pisałem to zadanie Ma być pole równe 136,5 cm2
1 cze 12:31
Nienor: W wyższych postach pisało co innego, zasugerowałam się tamtym.
Po prostu twój kalkulator (albo i Ty

) nie umie liczyć
| | 136,5*14450 | | 1972425 | |
c2= |
| = |
| =1806,25
|
| | 1092 | | 1092 | |
c=
√1806,25=42,5
1 cze 12:34
BARTEK: Dobrze to zrobiłem tylko źle użyłem kalkulatora

c
2=1806,25
c= 42,cm
a= 6,5 cm
b= 42 cm
1 cze 12:42
BARTEK: Czy mój sposób liczenia jest pracochłonny ?
1 cze 12:43
Nienor: Widziałam bardziej pracochłonne pomysły. O ile liczby znośne, lub masz kalkulator, to nie jest
zły.
1 cze 12:45
BARTEK:
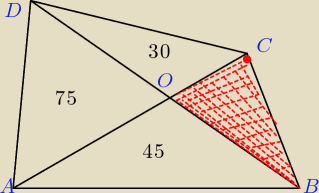
Przekątne czworokąta dzielą ten czworokąt na cztery trójkąty, Dane są pola trzech trójkątów
(zobacz rysunek).Oblicz pole czwartego trójkąta.
Zapraszam
1 cze 12:50
BARTEK: Próbowałem zapisałem pól strony dziwnymi obliczeniami ale nic z tego. Potrzebuję pomocy.
1 cze 13:26
BARTEK: −
1 cze 13:35
krystek: Przeszukaj na forum w tym tyg było liczone. Wyprowadź wysokości!
1 cze 13:41
krystek:
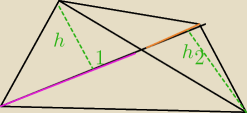
_
1 cze 13:47
BARTEK: 75x=1350
x=18
Wynik jest dobry ale z jakiego to prawa , twierdzenia to wynika nie wiem. Ktoś wie dlaczego
tak?
1 cze 13:56
1 cze 13:59
1 cze 14:02
BARTEK: Nie rozumie jak to sie nazywa?
1 cze 14:03
Nienor: Nazywa

1 cze 14:04
BARTEK: z czego to wynika

1 cze 14:51
Nienor: Te trójkąty mają wspólne podstawy, więc ich pola są proporcjonalne względem wysokości.
1 cze 14:54
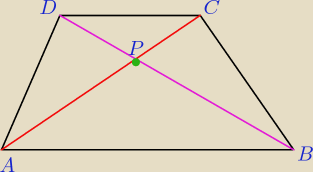
BARTEK:
Dzięki
zad 6.
W trapezie ABCD, AB || DC, poprowadzono przekątne , które przecięły się w punkcie P.
Wykaż ,że pola trójkątów BCP i APD są równe.
1 cze 15:38
BARTEK: PΔ ADB = PΔ ACB
PΔ ADB = PΔ APB + PΔ APD
PΔ ACB = PΔ BCP + PΔ APD
PΔ APB + PΔ APD = PΔ BCP + PΔ APD / − PΔ APD
PΔ APB = PΔ BCP
1 cze 15:59
vitek1980:
Popatrz na trójkąty ACD i BCD. Mają równe pole, ponieważ ich wspólną podstawą jest bok CD i oba
mają wysokość równą wysokości trapezu. Teraz odcinamy ich wspólną część czyli trójkąt CPD.
PADC=PBCD
PADC−PCPD=PBCD−PCPD
PAPD=PBCP
1 cze 16:03
BARTEK:
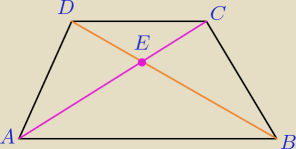
Zad 7.
W trapezie ABCD, AB || DC, poprowadzono przekątne , które przecięły się z punkcie E. Pola
trójkątów ABE i BCE są odpowiednio równe 78 i 52. Oblicz pole trójkąta CDE.
1 cze 16:19
BARTEK: PΔ ABE = 78
PΔ BCE = 52
PΔ ABC = PΔ ABE + PΔ BCE = 130
| | 1 | |
PΔ ADB = |
| |AB| * h = PΔ ABC |
| | 2 | |
PΔ ADE = PΔ ABC − PΔ ABE = PΔ BCE
| PΔ ADE | | PΔ CDE | |
| = |
| |
| PΔ ABE | | PΔ BCE | |
| | PΔ ADE * PΔ BCE | |
PΔ CDE = |
| |
| | PΔ ABE | |
ZROBIONE! W ciągu 2 dni jestem o niebo lepszy w rozwiązywaniu tych zadań!
1 cze 16:37
BARTEK: Zad 8.
W trapezie ABCD, AB || DC, przekątne przecinają się w punkcie E. Wiedząc ,że pola trójkątów ABE
i CDE są odpowiednio równe 90 cm2 i 40cm2, oblicz pole trójkąta AED.
Zapraszam!
1 cze 17:10
Mila: A jakie Ty masz propozycje?
1 cze 17:40
Mila: Wskazówka :
1) Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa.
2) skorzystaj z rysunku Krystek (chodzi o wysokość) z gdoziny 13: 47.
Jeśli masz odpowiedź, to będziesz wiedział, czy dobrze obliczyłeś.
1 cze 17:49
BARTEK: Zabieram się do pracy dzięki za rady Krystek

2 cze 20:33
BARTEK: Zabieram się do pracy dzięki za rady Krystek

2 cze 20:33
BARTEK:
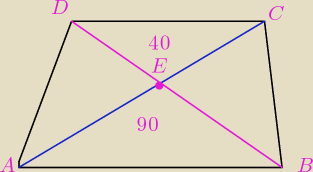
PΔ ABE = 90 cm
2
PΔ CDE = 40 cm
2
| PΔ DAE | | PΔ CDE | |
| = |
| |
| PΔ ABE | | PΔ BCE | |
| | 1 | |
PΔ ABD = |
| |AB| * h = PΔ ABC |
| | 2 | |
PΔ DAE + PΔ ABE = PΔ BCE + PΔ ABE
PΔ DAE = PΔ BCE
| PΔ DAE | | PΔ CDE | |
| = |
| |
| PΔ ABE | | PΔ DAE | |
PΔ DEA
2 = PΔ ABE * PΔ CDE
PΔ DEA
2 = 90 cm
2 * 40 cm
2
PΔ DEA
2 = 3600 cm
4
PΔ DEA = 60 cm
2
2 cze 21:21
BARTEK: Zad 9.
Punkt E jest punktem przecięcia przekątnych trapezu ABCD, gdzie AB || DC.
Pola trójkątów ABE i CDE są odpowiednio równe P1 P2 . Niech P oznacza pole trapezu ABCD.
Wykaż ,że P=(P1 + P2)2
Jak to zrobić zrobić ?!
2 cze 21:27
5-latek : To moze zacznij od rysunku
2 cze 22:24
BARTEK:
| | (a1 * k+a1)(h1 * k+h1) | |
P= |
| |
| | 2 | |
| | P1 | | P1 | |
P=P2* ( |
| +2√ |
| +P2 |
| | P2 | | P2 | |
P=P
1 +2
√P1*P2 + P2
P= (
√P1+
√P2)
2
2 cze 22:26
BARTEK:
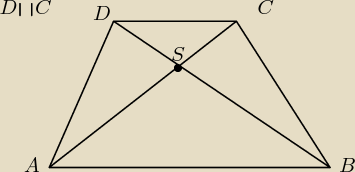
Trójkąty Δ CDS i Δ ABS są zawsze do siebie podobne jeżeli DE || AB ?
2 cze 22:31
Mila:
DC||AB ,
ΔDCS∼ΔABS cecha kkk
∡DSC=∡ASB jako kąty wierzchołkowe.
∡CAB=∡ACD jako kąty naprzemianległe wewnętrzne
∡ABD=∡BDC jako kąty naprzemianległe wewnętrzne
2 cze 22:38
BARTEK: A no tak

DZIĘKI MILA.
Kurcze znam to forum od dawna i muszę przyznać ,że tą strona istnieje tylko dzięki grupie ok.
20 osób.Fajnie

Może i ja kiedyś dostane kolorowy nick.

2 cze 22:44
BARTEK:
 Ok dzisiaj pisałem sprawdzian i dostanę piątkę. Dzięki wszystkim za pomoc szczególnie Basi
Ok dzisiaj pisałem sprawdzian i dostanę piątkę. Dzięki wszystkim za pomoc szczególnie Basi
W środę piszę sprawdzian z trygonometrii ,więc...
Trygonometria
Zad 1.
Oblicz wartości trygonometryczne dla kąta α.
3 cze 13:29
3 cze 13:31
krystek: ok
3 cze 13:33
BARTEK:
 Dziękuje za sprawdzenie
Dziękuje za sprawdzenie
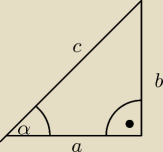
Zad 2.
Korzystając z danych w trójkącie na rysunku poniżej, oblicz wysokość h z dokładnością do 0,1
cm.
3 cze 13:41
3 cze 13:45
3 cze 13:53
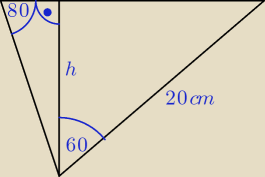
BARTEK:
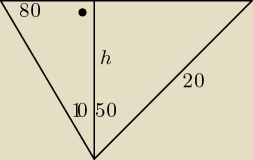 Błąd Kąt 60 stopni sięga do przeciwprostokątnej
Błąd Kąt 60 stopni sięga do przeciwprostokątnej
180 −(90+80)=10
cos 50 * 20 = h
0,643 * 20 = h
12.86 cm = h
3 cze 13:55
krystek: ≈12,9 jak masz podane w poleceniu.
3 cze 14:04
BARTEK:
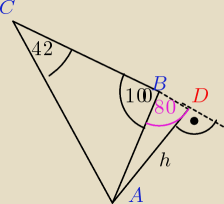
Zad 3.
Dziękuje
Oblicz obwód trójkąta ABC na rysunku z dokładnością do 0,5 cm:
h = 8 cm
|AB| = 8,12=8 cm
z Δ ADC
| | h | | |CD| | |
tg 42 = |
| cos 42 = |
| |
| | |CD | | |CA| | |
| | h | | |CD | |
|CD| = |
| |CA| = |
| |
| | tg 42 | | cos 42 | |
| | 8 | | 7 | |
|CD| = |
| |CA| = |
| |
| | 1,111 | | 0,669 | |
|CD| = 7,20 = 7 cm|CA| = 10,46 = 10.5 cm
LΔ ABC = |AB| + |CA| + |CB|
|CB| = |CD| − |BD| LΔ ABC =8 cm + 10,5 cm + 6 cm
| | h | |
tg 80 = |
| LΔ ABC = 24,5 cm |
| | |BD| | |
|BD| = 1,41= 1cm
|CB| = 7 − 1
|CB| = 6 cm
Dobrze ? 
3 cze 14:44
krystek: "rachunków " nie sprawdzam ,sposób ok
3 cze 14:56
c[BARTEK]:
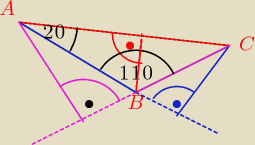 Dzięki.
Dzięki.
Zad 4.
Oblicz wszystkie wysokości na rysunku poniżej z dokładnością do 0,1 cm.
Wysokości dorysowałem.
3 cze 15:18
c[BARTEK]: |BC| = 10
3 cze 15:19
c[BARTEK]: ∡BCA = 180 − (110+20) = 50
h = |BC| * sin 50
h = 10 * 0,766
h = 7,66 = 7,7 cm
h = |BC| * sin 80
h = 10 * 0,985
h = 9,85 = 10 cm
h = |BA| * sin 80
h = 22.1769005848 = 22.2 cm
Z dnia na dzień czuję się mądrzejszy.
3 cze 15:42
Mila:
Załóż nowy wątek, bo długo się przewija.

3 cze 16:02
BARTEK: 
3 cze 17:55
BARTEK:
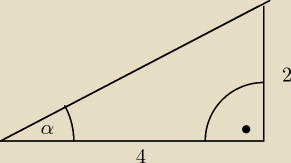
zad 5. Wykorzystując dane z rysunku powyżej :
a) 1 + * sinα * cosα
b)(tgα * cosα + ctgα * sinα)
2
4 cze 16:58
BARTEK: Może to ktoś zrobić bo cały czas wychodzą mi inne wyniki ?
4 cze 17:14
BARTEK: Czy ktoś na tym forum wgl jest?
4 cze 17:39
Nienor: Ale co z tym zrobić, obliczyć wartości

| | 2 | | 4 | | 8 | | 2 | |
a=1* |
| * |
| = |
| = |
|
|
| | √16+4 | | √16+4 | | 20 | | 5 | |
| | 1 | | 2 | | 3 | | 9 | |
b=(sinα+cosα)2=( |
| + |
| )2=( |
| )2= |
| |
| | √5 | | √5 | | √5 | | 5 | |
4 cze 18:34
BARTEK: Dzięki

4 cze 18:44
4 cze 21:07
 tak.
tak.

 x=a−r
y=b−r
x+y = c
a−r+b−r=c
a+b−c = 2r
stąd masz
a+b−c = 14
drugie równanie z sinusa
trzecie z Pitagorasa
no i układ
x=a−r
y=b−r
x+y = c
a−r+b−r=c
a+b−c = 2r
stąd masz
a+b−c = 14
drugie równanie z sinusa
trzecie z Pitagorasa
no i układ

 a=3k, b=4k, c=5k
3k/5k=3/5=sinα
r=7
r=(a+b−c)/2
7=(3k+4k−5k)/2
7=2k/2
7=k
stad a=3*7=21, b=4*7=28, c=5*7=35 najdłuższy bo to przeciwprostokątna więc:
P=1/2*21*28=294 cm²
a=3k, b=4k, c=5k
3k/5k=3/5=sinα
r=7
r=(a+b−c)/2
7=(3k+4k−5k)/2
7=2k/2
7=k
stad a=3*7=21, b=4*7=28, c=5*7=35 najdłuższy bo to przeciwprostokątna więc:
P=1/2*21*28=294 cm²


 b liczysz z tw.Pitagorasa
b2 = (85x)2 − (84x)2 = x2(852−842) = x2(85−84)(85+84) = 169x2
b = 13x
P = 84x*13x = 126,5
84*13*x2 = 126,5
z tego wylicz x
podstaw
a = 84x
b = 13x
c = 85x
i gotowe
b liczysz z tw.Pitagorasa
b2 = (85x)2 − (84x)2 = x2(852−842) = x2(85−84)(85+84) = 169x2
b = 13x
P = 84x*13x = 126,5
84*13*x2 = 126,5
z tego wylicz x
podstaw
a = 84x
b = 13x
c = 85x
i gotowe
 Dzięki Basia
w mojej szkole robimy innym sposobem chciałbym żebyście sprawdzili gdzie jest błąd proszę.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Dzięki Basia
w mojej szkole robimy innym sposobem chciałbym żebyście sprawdzili gdzie jest błąd proszę.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
 Powinno być 5,3 cm, 42 cm 42,5 cm
Co zrobiłem źle ?
Powinno być 5,3 cm, 42 cm 42,5 cm
Co zrobiłem źle ?
 ) nie umie liczyć
) nie umie liczyć

 Przekątne czworokąta dzielą ten czworokąt na cztery trójkąty, Dane są pola trzech trójkątów
(zobacz rysunek).Oblicz pole czwartego trójkąta.
Zapraszam
Przekątne czworokąta dzielą ten czworokąt na cztery trójkąty, Dane są pola trzech trójkątów
(zobacz rysunek).Oblicz pole czwartego trójkąta.
Zapraszam
 _
_


 Dzięki
zad 6.
W trapezie ABCD, AB || DC, poprowadzono przekątne , które przecięły się w punkcie P.
Wykaż ,że pola trójkątów BCP i APD są równe.
Dzięki
zad 6.
W trapezie ABCD, AB || DC, poprowadzono przekątne , które przecięły się w punkcie P.
Wykaż ,że pola trójkątów BCP i APD są równe.
 Zad 7.
W trapezie ABCD, AB || DC, poprowadzono przekątne , które przecięły się z punkcie E. Pola
trójkątów ABE i BCE są odpowiednio równe 78 i 52. Oblicz pole trójkąta CDE.
Zad 7.
W trapezie ABCD, AB || DC, poprowadzono przekątne , które przecięły się z punkcie E. Pola
trójkątów ABE i BCE są odpowiednio równe 78 i 52. Oblicz pole trójkąta CDE.


 PΔ ABE = 90 cm2
PΔ CDE = 40 cm2
PΔ ABE = 90 cm2
PΔ CDE = 40 cm2
 Trójkąty Δ CDS i Δ ABS są zawsze do siebie podobne jeżeli DE || AB ?
Trójkąty Δ CDS i Δ ABS są zawsze do siebie podobne jeżeli DE || AB ?
 DZIĘKI MILA.
Kurcze znam to forum od dawna i muszę przyznać ,że tą strona istnieje tylko dzięki grupie ok.
20 osób.Fajnie
DZIĘKI MILA.
Kurcze znam to forum od dawna i muszę przyznać ,że tą strona istnieje tylko dzięki grupie ok.
20 osób.Fajnie  Może i ja kiedyś dostane kolorowy nick.
Może i ja kiedyś dostane kolorowy nick. 
 Ok dzisiaj pisałem sprawdzian i dostanę piątkę. Dzięki wszystkim za pomoc szczególnie Basi
W środę piszę sprawdzian z trygonometrii ,więc...
Trygonometria
Zad 1.
Oblicz wartości trygonometryczne dla kąta α.
Ok dzisiaj pisałem sprawdzian i dostanę piątkę. Dzięki wszystkim za pomoc szczególnie Basi
W środę piszę sprawdzian z trygonometrii ,więc...
Trygonometria
Zad 1.
Oblicz wartości trygonometryczne dla kąta α.
 Dziękuje za sprawdzenie
Zad 2.
Korzystając z danych w trójkącie na rysunku poniżej, oblicz wysokość h z dokładnością do 0,1
cm.
Dziękuje za sprawdzenie
Zad 2.
Korzystając z danych w trójkącie na rysunku poniżej, oblicz wysokość h z dokładnością do 0,1
cm.
 Błąd Kąt 60 stopni sięga do przeciwprostokątnej
180 −(90+80)=10
Błąd Kąt 60 stopni sięga do przeciwprostokątnej
180 −(90+80)=10
 Zad 3.Dziękuje
Oblicz obwód trójkąta ABC na rysunku z dokładnością do 0,5 cm:
h = 8 cm
Zad 3.Dziękuje
Oblicz obwód trójkąta ABC na rysunku z dokładnością do 0,5 cm:
h = 8 cm

 Dzięki.
Zad 4.
Oblicz wszystkie wysokości na rysunku poniżej z dokładnością do 0,1 cm.
Wysokości dorysowałem.
Dzięki.
Zad 4.
Oblicz wszystkie wysokości na rysunku poniżej z dokładnością do 0,1 cm.
Wysokości dorysowałem.


 zad 5. Wykorzystując dane z rysunku powyżej :
a) 1 + * sinα * cosα
b)(tgα * cosα + ctgα * sinα)2
zad 5. Wykorzystując dane z rysunku powyżej :
a) 1 + * sinα * cosα
b)(tgα * cosα + ctgα * sinα)2

