logarytmy Paweł: 1. log(x−3)−log(2−x)=log(x2 −4) Mógłby ktoś rozwiązać to równianie opisując punkt po punkcie?

Ajtek: 196691 dubel

PuRXUTM: po pierwsze założenia 1) popatrz do tablic i napisz i jeszcze pytanie, to jest log(x−3)−log(2−x)=log(x²−4)

PuRXUTM: Witaj Ajtek

Paweł: tak Purxtum, ale proszę kogoś żeby to napisał tak jakby sam to rozwiązywał, ponieważ musze się tego do jutra nauczyć

PuRXUTM: najlepiej się uczy jak się samemu robi, więc mam propozycję: Pisz po kolei co robisz a my będziemy w razie czego korygować więc pierwsze założenia, zerknij do tablic jak nie pamiętasz i napisz

Ajtek: PuRXUTM witałem się z Tobą tutaj 196715 . Ale cześć .

PuRXUTM: nie zauważyłem, sory, a tam miałem źle ?

PuRXUTM: a no w sumie zero domknięte...

Ajtek: Nie domknąłeś przedziału przy 0.

Paweł: no wyznaczam dziedzinę x−3>0 2−x>0 x² −4>0 x>3 x<2 x>2 x<−2 dochodzę do momentu (x−3/2−x)= x² −4 i dalej nie wiem co robić. I pytanie dodatkowe jak mam w mianowniku 2−x to mogę wszystko przez to przemnożyć żeby usunąć niewymierność, czy trzeba jakiś inny sposób?

PuRXUTM: ale wyznacz tą dziedzinę bo jak na razie to wypisałeś założenia

Paweł: x∊(−∞,2) ∪ (2,+∞) DOBRZE? potem nie wiem co robić i ponawiam pytanie z przemnażaniem

PuRXUTM: z tego co widzę to D=∅ ale ja się nie znam, może niech się ktoś wypowie...

Paweł: a następne mam mistrzu log (x+1)/(2x−3)≥0 to x∊<−1,+∞) i nie wiem co dalej robić, zacinam się wszędzie przy tym, jak możesz napisz mi co z tym dalej się robi, jak się tą niewymierność usuwa. Prosze Cię

asdf: no bo Ci pisałem, zebys wyznaczyl dziedzine...ale ty nie − wiesz lepiej.No to siedz i to rozwiązuj.

PuRXUTM: no ale to nie powód żeby przeklinać... po za tym powinieneś się cieszyć, na założeniach kończy się zadanie

asdf: tutaj dziedziny nie masz x + 1 > 0, cyzli x > −1... log_ab a > 0 a ≠ 1 b > 0

	x+1		a
czyli nie x+1 > 0 tylko		> 0 ⇒ i tu masz taki wzór:		> 0 jest równoważne z:
	2x−3		b

a* b > 0, gdy b ≠ 0 (to oczywisce − nie mozna dzielic) − wnioski wyciągnij.

Paweł: czyli mnoże (x+1)(2x−3)= 2x² −x+3, wyliczam deltę i x1 i x2?

PuRXUTM: po co przecież masz (x+1)(2x−3)>0 rysujesz wykres bo miejsca zerowe "widać" x=−1 v x=1,5

Paweł: tak samo robiłem ale w odpowiedziach jest że x∊(−1,5;4>..........

Paweł: log₃ 3/(3x−1)> log₃ (5−x) to bd że x∊(1,5)

PuRXUTM:

	1
że dziedzina x∊(		,5)
	3

przecież to normalnie robisz

	3
1)		>0 i 2) 5−x>0
	3x−1

	3
1)		>0 /*(3x−1)2
	3x−1

3(3x−1)>0 /:3 3x−1>0 3x>1

	1
x>
	3

2) x<5

	1
Więc D=(		,5)
	3

Paweł: coś dalej się z tym robi, czy tak zostawia? odpowiedź w zbiorze jeszcze inna x∊(1,2) suma (4,5)

PuRXUTM: ale odpowiedź, czy dziedzina, bo ja na razie dziedzinę obliczyłem

Paweł: odpowiedź, a ja cb proszę żebyś pokazał mi sposób robienia tych zadań do końca

asdf: Paweł, nie chce Ciebie niezniechęcać − wręcz przeciwnie. Do jutra tego nie ogarniesz dobrze Ale wyciągnij wnioski, usiądź do matematyki, pisz zadania na forum, a na pewno Tobie nie jeden pomoze (jak będę mieć czas to i ja Tobie pomoge − nie ma problemu). Początki mogą być trudne − a nawet będzie dobrze jak będą − ale jak poznasz podstawy to już z górki

Paweł: tak, ale ja tego potrzebuje na jutro, pokażcie mi tylko sposób, jutro mam poprawkę z matematyki..... 3klasa.

Paweł: a uwierz jestem zdolny, po prostu potrzebuje zadania rozwiązanego od początku do końca, wtedy wzoruje się na tym i jest dobrze. PROSZĘ WAS

PuRXUTM: https://matematykaszkolna.pl/strona/1702.html

PuRXUTM: https://matematykaszkolna.pl/strona/1703.html

Mila: To, co w końcu chcesz wiedzieć, tyle tu komentarzy. Napisz problem.

Paweł: Jedną z najważniejszych rzeczy jest jak mogę usunąć niewymiernośc z mianownika. I ten przykład porządnie zrobiony log3 3/(3x−1)> log3 (5−x)

Krzysiek: https://matematykaszkolna.pl/strona/1635.html −−−−−−usuwanie niewymiernosci z mianownika

PuRXUTM:

	1		8−2√10		8+2√10
mi wyszło w tym zadaniu z log taka odp x∊(		;		) U (		;5)
	3		3		3

Krzysiek: https://matematykaszkolna.pl/forum/196447.html zobacz tez tutaj co do usuwania niewymiernosci

asdf:

	3
log3(		) > log3(5−x)
	3x−1

	3
log3(		) − log3(5−x) > 0
	3x−1

	3		1
log3(		*		) > 0
	3x−1		5−x

	3		1
log3(		*		) > log31
	3x−1		5−x

3		1
	*		> 1
3x−1		5−x

3−(3x−1)(5−x)
	> 0
(3x−1)(5−x)

3−15x+3x2+5−x
	> 0
(3x−1)(5−x)

(3x²+8−16x)(3x−1)(5−x) > 0 z pierwszego wychodzą pierwiastki:

	2
x1 =		(4+√10)
	3

	2
x2 =		(4−√10) (zwykla delta − policzysz sobie)
	3

pozniej masz

	1
(3x−1) = 0, x =
	3

5−x = 0, x = 5

	1		2		2
x ∊ (		;		(4−√10) v (		(4+√10);5)
	3		3		3

Miałeś rysowanie funkcji stopnia większego jak 2?

Paweł: według zbioru tak powinno być x∊(1,2) suma (4,5), ale zauważyłem, że ten zbiór PAZDRO często ma błędne odpowiedzi

asdf: No to jak nie znasz podstaw a probujesz robic zadania ze zbioru PAZDRO to pozdro...zacznij od postszych

PuRXUTM: nie pozdro tylko PAZDRO

Paweł: nie, nie miałem, ale wszystkim bardzo dziękuję, większość już umiem. tylko jeszcze jedna rzecz, jak zabrać się do takiej dziwnej nierówności log₁/3[log₄(x²−5)]>0

Paweł: muszę robić zadania z PAZDRO, ponieważ taki mam w szkole i z niego nauczycielka da mi zadania

PuRXUTM: a jaka jest odp. ? bo mi wyszło że x∊(−3,−√5)U(√5;3)

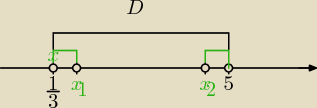
Mila: Wpisz zadania z niewymiernością, ja tymczasem napiszę z logarytmem.

	3
log3		> log3 (5−x)
	(3x−1)

Dziedzina: 3*(3x−1)>0 i 5−x>0⇔ 3x>1 i 5>x⇔

	1		1
x>		i x<5⇔D=(		,5)
	3		3

	3
log3		> log3 (5−x) funkcja log3(x) rosnąca
	(3x−1)

3
	>5−x⇔
(3x−1)

3
	−(5−x)>0
3x−1)

3−(5−x)(3x−1)
	>0
3x−1

3−(15x−5−3x2+x)
	>0
3x−1

3x2−16x+8
	>0 trzeba rozłożyć licznik na iloczyn
3x−1

Δ=256−4*8*3=160 √160=4√10

	16−4√10		16+4√10
x1=		lub x2=
	6		6

	8−2√10		8+2√10
x1=		≈0,6 lub x2=		≈4,8
	3		3

3x2−16x+8
	>0⇔
3x−1

(x−x₁)(x−x₂)(3x−1>0 i x∊D⇔

	1		8−2√10		8+2√10
x∊(		,		)U(		,5)
	3		3		3

coś musiałeś zmienić w równaniu, bo nie wychodzi jak w odpowiedzi, a może ja coś inaczej przepisałam.

Paweł: x∊(−3,−√6) suma (√6,3)

PuRXUTM: no dobra, zgadza się rozpisać Ci to ?

Paweł: tak, poprosiłbym

Paweł: Powiem Wam, że jednak matematyka nie jest trudna, od godzin 16−20 i od 22−24, nauczyłem się tych logarytmów od podstaw i np. wszystkie zadanka z tej strony internetowej zrobiłem, myślę że zaliczę jutro to. DZIĘKUJE WAM

PuRXUTM: po pierwsze.... założenia mamy log_1/3(log₄(x²−5))>log_1/31 ponieważ log_1/31=0 więc zał: log₄(x²−5)>0 log₄(x²−5)>log₄ 1 ⇔ x²−5>1 x²>6 x∊(−∞;−√6) U (√6;+∞) i jeszcze założenie x²−5>0 ( bo mamy log₄(x²−5) ) x²>5 x∊(−∞;−√5) U (√5;+∞) dziedzina jest częścią wspólną x∊(−∞;−√5) U (√5;+∞) i x∊(−∞;−√6) U (√6;+∞) czyli D=(−∞;−√5) U (√5;+∞) teraz rozwiązujemy log_1/3(log₄(x²−5))>log_1/31 ⇔

	1
log4(x2−5)<1 ( zmieniamy zwrot nierówności bo		jest mniejsze od 1 )
	3

log₄(x²−5)<log₄ 4 ⇔ x²−5<4 x²<9 x∊(−3;3) teraz zestawiamy z D i mamy że x∊(−3;−√6) U (√6;3)

PuRXUTM: czyli chyba nie potrzebnie pisałem...

Paweł: dzięki

Mila: 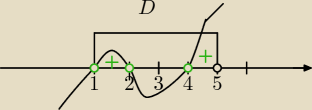No to Paweł źle przepisałeś ten przykład, w mianowniku jest( x−1) a nie (3x−1)

	3
log3		>log3(5−x)
	x−1

D:

3
	>0 i x−1≠0 i 5−x>0⇔
x−1

x−1>0 i 5>x⇔x>1 i x<5 D=(1,5)

3
	>5−x⇔
x−1

3
	−(5−x)>0
x−1

3−(5−x)(x−1)
	>0
x−1

3−(5x−5−x2+x
	>0
x−1

U{x²−6x+8}{x−1)>0 zamiast znak ilorazu badamy znak iloczynu: (x²−6x+8)(x−1)>0 i x∊D Δ=36−4*8=4

	6−2		6+2
x1=		lub x=
	2		2

x₁=2 lub x₂=4 (x−2)(x−4)(x−1)>0 i x∊D x∊(1,2)U(4,5)

Paweł: potrzebnie, czekałem na to

Mila: ?

Paweł: tak Mila, źle przepisałem mój błąd. Teraz dziękuje Wszystkim raz jeszcze i życzę miłej nocy

Mila: Powodzenia.

Paweł: zaliczone na 4

Krzysiek: Fajnie . To teraz dawaj na forum zadania z usuwania niewymiernosci

Mila: Gratulacje.