Gustlik: Proponuję prosty wierszyk: W pierwszej wszystkie są dodatnie, w drugiej tylko sinus, w trzeciej tangens i cotangens, a w czwartej cosinus. O wiele łatwiejszy do nauczenia i przyswojenia, niż tabelka znaków.

Zbyś: Po pierwszej ćwiartce wszyscy stoją, po drugiej tylko sinus, tg i ctg budzą się na trzecią, sin zasypia, cos wstaje, widzi, że wszyscy leżą, dopija czwartą Wiersz nie jest mojego autorstwa, tylko nauczyciela

ksywa: W pierwszej ćwiartce same plusy W drugiej tylko sinus W trzeciej tangens i kotangens A w czwartej kosinus!

Gustlik: Nie, no Zbysiu, zaje....sty wiersz ) Matematyka na wesoło )

Szopen: Haha, dobre z tą wódką

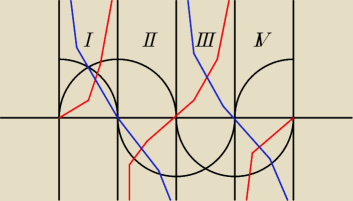
Szopen: Nie rozumiem za bardzo po co przedstawiony jest rysunek z ćwiartkami układu kartezjańskiego skoro przecież nie o te ćwiartki chodzi. Według mnie powinno to wygladać tak jak na rysunku tylko ze troche on krzywy bo od ręki ale wtedy wszyscy wiedzą o co biega. Pozdrawiam.

Jakub: Jak najbardziej chodzi o ćwiartki z układu kartezjańskiego. Na wykresie sinusa i cosinusa, który narysowałeś, też je widać. Jednak rysując układ współrzędnych miałem na myśli definicję funkcji trygonometrycznych ze strony 417.

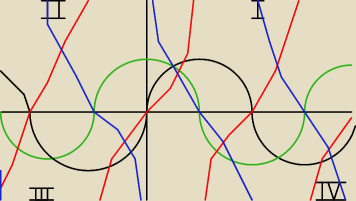
KKSzop: Nie rozumiem za bardzo dlaczego chodzi o tamte ćwiartki. Więc narysowałem i mi tu nie odpowiada: W pierwszej wszystkie są dodatkie: ok W drugiej tylko Sin i już mi nie pasuje bo miejscami też wszystkie są dodatnie. Reszta to samo. Prosiłbym o wytłumaczenie co to ma do ćwiartek kartezjańskich ?

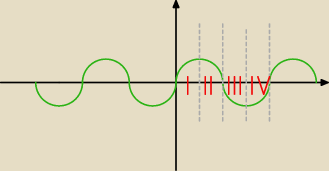
Jakub: Popatrz na rysunek na stronie 417. Masz tam kąt α. Widzisz? Jak będziesz zwiększał ten kąt to drugie ramię kąta (to z punktem P), będzie przechodziło przez kolejne ćwiartki I, II, III, IV. Mam nadzieję, że już widzisz, że pierwsza ćwiartka odpowiada kątom z przedziału (0,90^o), druga (90^o,180^o), trzecia (180^o, 270^o), czwarta (270^o,360^o). Te same przedziały w mierze łukowej (0,^π₂), (^π₂,π), (^3π₂,2π). Zobacz one są w tabelce na stronie 451. Na podstawie wzorów pod rysunkiem na stronie 417 można policzyć sin, cos, tg i ctg kąta bez względu w której ćwiartce jest drugie ramię. Tylko ciężko jest z tych wzorów ustalić znak kąta. Tzn. według mnie łatwo, ale chyba jest to trudne jak ludzie sobie wierszyki wymyślają Ja zaproponowałem sposób, aby dostrzegać te znaki na wykresach funkcji trygonometrycznych. Zobacz na wykres sinusa wyżej lub na stronie 426. Pierwsza ćwiartka to przedział (0,90^o)=(0,^π₂) czyli jak widać sinus dodatni. Druga ćwiartka to przedział (90^o,180^o)=(^π₂,π) czyli jak widać sinus dodatni. Trzecia ćwiartka to przedział (180^o,270^o)=(π,^3π₂) czyli jak widać sinus ujemny. Czwartka ćwiartka to przedział (270^o,360^o)=(^3π₂,2π) czyli jak widać sinus ujemny. To wszystko widać na wykresie, nie trzeba się uczyć wierszyków lub tabeli na pamięć. Ty natomiast poszedłeś na skróty. Umieściłeś na wykresie sinusa oznaczenia ćwiartek i próbowałeś coś dostrzec. To nie te ćwiartki Nie można omijać wzoru. Ćwiartki to kąty, a kąty widać na osi poziomej. Jasne? Jak nie to pisz.

KKSzop: Dobra rozumiem teraz dzięki Czasem coś łatwego a nie chce pała zaczaić Pozdro

Magda: a wyjdzie tez znak plus czy minus rysując trokąt w kółku o promieniu jeden. u nas na uniw, tak robia ze jak ktos zapomni to mozna zawsze z tego wyjsc tylko ze my jeszcze sie uczymy tak ze np. sin 270^∧ →sin3π/2 →−1 ?

tom215: wierszyk z wódką wchodzi najlepiej, ciekawe czemu niby nic nie ma tam o wódce, a każdy zaczaił

aga: ctg w 4 ćwiartce ma znak ujemny, ale w co sie zamienia?

kkkasiula9: ja wole ten 1 wierszyk bo go znam

Matematyk1999: W pierwszej cwiartce stoi Plus. W drugiej leży Sinus. Dalej tangens i cotangens i cotangens oraz tangens Czwarta rzadzi cosinus!

mala: Proszę o pomoc mając np. −tgx=1 jaką wartosc otrzymam tgx=−π/4 czy inną i jak sprawa wygląda w podobnym przypadku tylko zamiast tg , gdy bedzie cos

licealistka: pierwsza ćwiartka jest dodatnia w drugiej tylko sinus w trzeciej tangens i cotangens a w czwartej cosinus....

monika: w jakiej ćwiartce leży kąt cos 19/4 π? bo mam to rozwiązane jako= cos (4π+ 3/4 π)= cos(π−π/4)= cos π/4= − √2/2. tylko skąd ten minus ? ten kąt nie jest z 4 cw, gdzie cosinus jest dodatni ?

Jakub: Kąt ¹⁹₃π = 4π + ³₄π = 4*180^o + ³₄*180^o = 2*360^o + 135^o leży w drugiej ćwiartce. Kosinus tego kąta jest ujemny.

MarekT: W komentarzu z 28−08−2010 23:04 stoi: "Zobacz na wykres sinusa wyżej lub na stronie 427." na stronie 427 jest wykres ...cosinusa... i jak tego nie zauważysz, to nic się nie zgadza... bo wykres sinusa jest na stronie 426. ... 3 lata nikt nie zauważył ?

Jakub: Już poprawiłem. Może ktoś to wcześniej zauważył, ale tylko Tobie chciało się o tym napisać komentarz. Dzięki.

Mmm: Hej Jakub, nie wiem czy mój sposób się komuś przyda, ale mnie zaskoczyło to że nikt o tym tu jeszcze nie napisał (chyba, że czegoś nie doczytałam). Przecież te wartości funkcji trygonometrycznych stają się oczywiste, jeśli spojrzeć na to w ten sposób: patrzymy na cześć o trygonometrii z kart maturalnych, widzimy czarno na białym mini układ współrzędnych plus co przez co to sin,cos itd. i wtedy myślimy, w której ćwiartce co ma jaki znak:

	y		x		y		x
I ćwiartka: sinα =		cosα=		tgα=		ctgα=
	r		r		x		y

	y		−x		y		−x
II: sinα =		cosα=		(−) tgα=		(−) ctgα=		(−)
	r		r		−x		y

	−y		−x		−y		−x
III: sinα =		(−) cosα=		(−) tgα=		(+) ctgα=		(+)
	r		r		−x		−y

	−y		x		−y		x
IV: sinα =		(−) cosα=		tgα=		(−) ctgα=		(−)
	r		r		x		−y

Może piszę oczywistość, ale kto wie, może komuś się to przyda (bo jak widzę jeśli ludzie uczą się wierszykow żeby to zapamiętać, to może jednak nie do końca kumają jakie to jest logiczne)

Mmm: ahh, teraz widzę, że pobieżnie przeczytałam te komentarze tutaj, bo tłumaczysz to na początku komuś.

Jakub: Dokładnie. Wierszyki wierszykami, ale to widać, albo ze wzorów, tak jak napisałaś, albo z wykresów funkcji trygonometrycznych.