Adam: Dlaczego zakładamy, że P jest odległe o 2 od układu współrzędnych ?

Jakub: Jakąś liczbę trzeba było wybrać. Padło na 2. Można też wybrać np. 6 i wtedy z twierdzenia Pitagorasa będziesz miał y²+3²=6² itd.

'AjnsztaJn':D: 1 i 2 przykład rozumiem, ale 3 i 4 nie za bardzo... nie można zrobic w taki sam sposób 3 i 4 tak, jak dwa pierwsze? proszę o odpowiedź

Jakub: Trudno powiedzieć. Wydaje mi się, że najprościej jak można to zrobiłem.

Ola:

	1
A co gdyby moje x =1? Wtedy cosinus 120 stopni wynosiłoby		, tg i ctg zresztą też byłyby
	2

dodatnie. Dlaczego tak nie można zrobić?

Ola: Mam na myśli to, gdybym punkt P narysowała po drugiej stronie i wynosiłby on (1,2), a nie (−1,2).

ahu8: Ola, obliczamy wart. dla kąta 120. Gdyby to był kąt 0<kąt<90 to wart. x i y byłyby dodatnie, bo ramię znajdowałoby się w pierwszej ćwiartce. A tu mamy 120, więc ramię jest w drugiej ćwiartce i watr. x musi być ujemna.

xzc: Dlaczego do obliczenia kąta 135 i 225 stopni wybieramy dowolny punkt P a w przypadku 2 ostatnich przykładów takie rozwiązanie nie wchodzi w grę?

Jakub: W tych dwóch ostatnich rozwiązaniach punkt P też może leżeć w dowolnym miejscu na drugim ramieniu kąta. Dopisałem to już do rozwiązania. Dzięki.

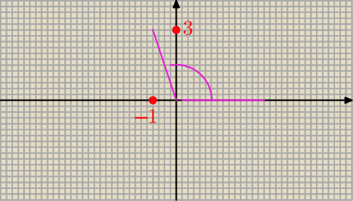
Mmm: Czemu taki tok myślenia się nie sprawdza?

	30
1. Wiemy, że potrzebujemy 30 stopni z II ćwiartki. II ćwiartka ma 90 stopni.		to
	90

stosunek 1 : 3. 2. Dobieram więc punkty x= −1 i y = 3 żeby tą proporcję zachować. Wygląda to wtedy na kąt 120stopni... Niestety, w rozwiązaniach dalej się nie zgadza, r wychodzi √10, a więc wiadomo że inne też się sypią. Dlaaaczeggooo mój sposób jest niedobry, przecież jest tak logiczny :'−( ...

Mmm: Oczywiście na oko widzę że to jest niedobre i rozumiem Twoją metodę Jakubie, ale w sumie nie dokońca rozumiem czemu nie można tak wykombinować jak powyżej

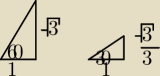
Jakub: Twoje rozumowanie jest logiczne, ale oparte na błędnym założeniu. Przyjmujesz, że jak zmienisz kąt k razy to tak samo k razy zmieni się długość odcinków. Zakładasz, że długość odcinków zmienia się proporcjonalnie do zmiany kąta. Tak nie jest. Zobacz na mój rysunek. Pierwszy trójkąt ma przyprostokątne 1 i √3 ≈ 1,732

	√3
Drugi trójkąt ma przyprostokątne 1 i		≈ 0,577
	3

Jeżeli pierwsza przyprostokątna jest równa 1, to te drugie muszą wynosić tyle ile wyżej

	√3
napisałem, bo tg60o = √3, tg30o =		(zobacz 397).
	3

Według twojego założenia zmniejszenie kąta dwukrotnie powinno spowodować zmniejszenie długości drugiej przyprostokątnej dwukrotnie a tak nie jest.

1,732
	= 0,866 ≠ 0,577
2

Widzisz, twoje początkowe założenie okazało się inwalidą. Widać, to też na wykresie każdej funkcji trygonometrycznej. Przykładowo masz wykres sinus 426. Od 0 do ^π₂ (czyli 90^o) masz fragment wykresu, który nie jest prostą. Początkowo nawet ją przypomina, ale później zagina się do poziomu. Jak nie ma prostej, nie można mówić o proporcjonalności, między kątami a długościami odcinków, które tworzą te kąty.

Mmm: Aha... Teraz już wszystko jasne Dziękuję, że pokazałeś mi czemu mój argument jest inwalidą! Tak na marginesie, widzę że jednak dopadły mnie geny taty 'na oko'. Kiedyś w podstawówce po dłuższej przerwie przyszłam do szkoły i totalnie nie kumałam jak oni dodają i odejmują te straszne ułamki o różnych mianownikach. Pytam więc taty jak to robić, a on na to −'no wiesz, na oko córeczko. Zobacz jakie to łatwe. Połowa i połowa to całość. Ćwierć i ćwierć to połowa'

	4		2
− 'no dobra, ale co np. z		−		? Ile to jest i jak to policzyć?'
	5		3

− 'hmm... no, to właśnie takie przykłady robimy 'na oko'.' (komiksowe 'Puff', nastąpił błysk i tata w magiczny sposób błyskawicznie zniknął)

Jakub: Sposób na oko nie jest taki zły Mi się przynajmniej kojarzy z racjonalnym podejściem do problemu. Próbą przełożenia abstrakcyjnego problemu na jakąś fizyczną sytuację. A że czasami prowadzi to do błędu, no cóż, tak czasami jest. Ale próba logicznego rozwiązania problemu została podjęta. To najważniejsze. Najgorsze podejście do matematyki, to jest, co mam zrobić, gdzie dodać, gdzie odjąć, bez wnikania, po co się tak robi. Takie bezmyślne, mechaniczne działania.

Mmm: Dzięki za feedback!

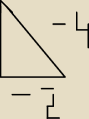
Arek: Czy r nie powinno być równe −4? Skoro tam jest −2 i ten bok to z wzoru będzie jako "a" a przeciwprostokątna to tak jakby "2a" czyli −2 x 2=−4

Jakub: Dobrze kombinujesz ze wzorów na długość boków trójkąta prostokątnego, gdzie jeden kąt ma 60^o. Te wzory są na 2280. Pamiętaj tylko o jednym. Długość odcinka (boku) NIGDY nie jest ujemna. Dlatego powinieneś wziąć a = 2, 2a = 4.