aaa: wyznacz najmniejszą wartość funkcji f (x) = −3x²+2x+1 w przedziale <− 1; 1>

Jakub: Zadania zamieszczaj na forum zadankowym.

nie zdam: dlaczego niektore zagadnienia nie maja objasnien jak je liczyc ?

Jakub: Jakie zagadnienia na przykład?

budzio: bardzo fajna strona

Nextion24: Dodałbym dział z rozwiązywaniem nierówności kwadratowych z wartością bezwzględną, a tutaj: https://matematykaszkolna.pl/strona/i4.html nie ma tego, a niektórym może się przydać Np. * x² − 3|x| − 4 <= 0 * x² − 4x + |x − 1| + 3 <= 0 * x² + 4x + |x − 3| + 5 > 0 * |x² + 6|x| + 9| <= 0 − a tutaj podwójna wartość bezwzględna * |x² + x − 12| − 6 => 0 Co do równań kw. z parametrem to bym dodał takie zadania: * Zbadaj dla jakich wartości parametru 'm' równanie: x² + mx + m + 1 = 0 ma co najmniej 1 rozw. * Dla jakich wartości parametru 'k' równanie x² + (3k − 1)x + k² − k + 1 = 0 ma 2 różne pierwiastki rzeczywiste dodatnie. Można by było też dać z ujemnymi, bo wtedy inne założenia są w wzorach Viete'a. * Dla jakich wartości parametru 'k' wartości funkcji f(x) = kx² + kx + k są dla każdgo argumentu 'x' mnijsze od odpowiednich wartości funkcji g(x) = (1 − k)x + 3

enkil: super strona!

Stach:): ja powiem tak. 23 sierpień mam komisa z matematyki. Na razie wszystko co potrzebuje się nauczyć jest tutaj. Dodam jeszcze, że jestem na profilu mat−fiz i tam naprawde jest dosyć ciężko i to co nie mogłem zjarzyć na lekcji teraz mi to łatwo przychodzi i gdybym wiedział o tej stronce wcześniej pewnie teraz bym był gdzieś na torze crossowym pełen szacuneczek dla Jakuba

Orion: Autorowi tej strony szczerze dziękuję z głębi serca, bez tej strony nauczenie się pewnych rzeczy przyszłoby dużo trudniej... Naprawdę − wielki szacun dla Kuby ^^

basiulek: Jak znależć wzór funkcji kwadratowej wiedząć ,że pierwiastkami są liczby 4 i −2 a wartość minimalna to −18. Proszę o pomysł bo napisałam układ trzech równań i nic mi nie wychodzi

xyz: ja prosiłabym jeżeli oczywiście jest tro możliwe o zamieszczanie zadań maturalnych działami np. funkcja liniow, kwadratowa itd.

Hubb: dobry czlowiek dzieki super strona

kermit: Nie obliczając pierwiastków (x1,x1) trojmianu x² − x − 6 wyznacz wartosc wyrazenia : x₁² − x₂²

humelix: Super strona

i czy lub?: a jest gdzieś wytłumaczone kiedy dajemy ∧ a kiedy ∪? bo nigdy przy rozwiązywaniu różnych równań, nierówności zwykłych czy też z wartością bezwględną tego nie wiem. Wiem tylko zę przy podaniu dziedziny jest zawsze spójnik "i". Bardzo proszę o wytłumaczenie mi tego.

Paulina:): hej potrzebuje pomocy czy ktos pomoze mi rozwiazac zadanie wykresem funkcji f(x)=x²+bx+c jest parabola o wierzchołku w punkcie W. wyznacz współczynnik b i c oraz podaj zbiór wartosci funkcji f. W(0,0). DZIEKUJE

Jakub: Napisz to zadanie na forum zadankowym.

Agata: przydałoby się przesuwanie funkcji kwadratowej...

Jakub: Przykłady przesuwania wykresu funkcji kwadratowej masz na 81, 83, 85.

POMOCY: Do poprawienia oceny końcowej z matematyki nauczycilka zadała mi pracę domową z którą mam problem. Prosiłabym o rozwiązanie z objaśnieniami... z góry serdecznie dziękuję 1) Przedstaw podaną postac funkcji kwadratowej w postac ogólną i kanoniczną. Naszkicuj wykres funkcji i wypisz wszystkie jej własności. 2) Przedstaw podaną postac funckji kwadratowej w postac ogólną i iloczynową. Naszkicuj wykres i wypisz wszystkie jej własności.

bartek: super strona szykuje sie na jej podstawie do matury z matmy zawsze z matematyką miałem problemy ale dzieki tej stronie jakoś to idzie

oktavius: PORSZĘ O POMOC JAK PODAĆ PIERWIASTKI RÓWNANIA ax³ + bx² + cx +d = 0. z Wikipedii nic za bardzo nie rozumiem. PLEASE POMÓŻCIE jakby ktoś wyjaśnił obrazowo wikipedię,to wielkie DZ

Jacek G.: Witam jestem dosyć "tępy" za matematyki. Głównie wywołane długa nieobecnością w szkole. Jutro piszę sprawdzian z matematyki, w związku tego mam pytanie.. Jak rozpoznać kiedy funkcja ma x² kiedy 2x² itd.

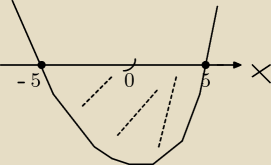
Aleksandra93: Hejka proszę zobaczcie czy dobrze zrobiłam zadania. FUNKCJA KWADRATOWA Wyznacz współczynniki b i c trójmianu y = x² + bx + c b) nieujemne tylko wtedy gdy |x| ≥ 5 . czyli zaczęłam tak (zobacz rysunek) − wtedy x ∊ <−5,5> , wzięłam te liczby za miejsca zerowe i z postaci iloczynwej policzyłam b i c y = (x−5)(x+5) i wyszło mi y= x² − 25 czyli b=0 a c = −25 dobrze

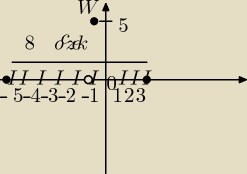
Aleksandra93: Zadanie kolejne. Wyznacz wartość funkcji f(x)= a(x−3)(x+5) jest równa 5. Wyznacz a oraz współrzędne wierzchołka. Czyli, miejsca zerowe, x₁= 3 x₂= − 5 największa wartość funkcji równa się 5. Funkcja osiąga największą wartość gdy a<0 a zarazem jest to q jedna z parametrów wierzchołka W(p,q). "p" można obliczyć bardzo łatwo, rysujemy wykres, zaznaczamy m.z liczymy odległość między nimi i dzielimy na pół mi wyszło −1. (rysunek ). Współrzędne wierzchołka postawiamy tutaj: y=a(x−3)(x+5) i wychodzi a a = −3,2 .............. co sądzicie?

Gustlik: Moje "poprawki" do programu z tego działu: podstawy rozszerzenia studia równanie kwadratowe, wzór na deltę, pierwiastki (miejsca zerowe) równania kwadratowego układy równań kwadratowych wzory Viete'a funkcja kwadratowa: postać ogólna, kanoniczna, iloczynowa wykres funkcji kwadratowej, współrzędne wierzchołka paraboli znajdowanie wzoru funkcji kwadratowej znajdowanie największej i najmniejszej wartości w przedziale wyznaczanie przedziałów monotoniczności funkcji kwadratowej wyznaczanie zbioru wartości funkcji kwadratowej nierówność kwadratowa równania i nierówności kwadratowe rozwiązywane graficznie równania i nierówności kwadratowe z parametrem równania i nierówności kwadratowe z wartością bezwzględną zadania tekstowe prowadzące do równań i nierówności z jedną niewiadomą zadania tekstowe − optymalizacyjne

xyz: Czy można by było zmienić barwy działów zadań rozszerzonych na pomarańczowe? Ludzie z niedowidzeniem barwnym mają teraz ogromny problem rozróżnić kolor działów rozszerzonego i podstawowego, a pomarańczowy kolor byłby zdecydowanie wyraźniejszy od obecnego ciemnoczerwonego (mylącego się z zielonym).

Jakub: Masz na myśli takie kolory jak zastosował Gustlik nad twoim wpisem? Zauważ też, że jak najedziesz kursorem pojawia się tło w odpowiednim kolorze.

Sonia!: Dziękuję autorowi − jesteś the best! pozdrawiam <3

violinistka: Dzięki Tobie rozumiem funkcję kwadratową! Wszystko wytłumaczone jest po kolei, w jasny, przejrzysty sposób. A nie tak jak bywa w szkole.... Bardzo dziękuję za pomoc

Aeven: Naprawdę świetna strona. Do tej pory nic nie umiałem z matematyki(obecnie chodzę do II klasy liceum profil MAT−INF). Próbowałem rozwiązać zadania w domu samodzielnie, lecz niec z tego Biłem się już nawet zeszytem po głowie ale nie miałem pojęcia jak się zabrać za różne zadania. Brawa dla pana Jakuba

Justyna: Świetna stona! Przyda się do powtórek przed maturą Przejrzysta, komunikatywna, wiedza w pigułce z dosadnym tłumaczeniem. Ogromne podziękowania dla twórcy strony

fryta70: Rozwiąż równanie: 4x²−(1−2x)²+2x=11

dancio: Jakub genialnie wszystko wytłumaczyłeś, jak dla mnie jesteś geniuszem

Domek: Witam Mam problem nie wiem jak wyliczyć pewne zadanie. Byłbym wdzięczny jakby mógł mi to ktoś wytłumaczyć: Znajdź wartość największą i najmniejszą funkcji: a) f(x)=−x²−2x w przedziale <0,2> b)f(x)=−2x²+4x+6 w przedziale <0,3>

Jakub: Zobacz 1683.

LUX: Bardzo dobra strona wiele można z niej się nauczyć , dzięki wielkie dla autora.

bartek: pomocy matma nierównosci −3xkwadrat+4x−5<0

Magda: Kuba czy Ty studiowales fizyke na Uniwersytecie Wroclawskim?

Jakub: Zgadza się. Studiowałem. Dawne czasy

Magda: KUBA RAZEM STUDIOWALISMY FIZYKE nie wiem czy mnie pamietasz....Magda Kowalska

Jakub: Pamiętam Chociaż nie jestem pewien. Trochę czasu upłynęło. Napisz do mnie maila jakub [małpka] matematyka.pisz.pl

Rafaello: Dobrze, ładnie maturke ładnie z ttego pewnie dobrze mozna napisac w kazdym razie moja nauka poiera sie w duzej mierze na tej stronie

justynka: przedstaw trójmian kwadratowy w postaci ogólnej y=−(x−4)2−3 y= −1/2(x−2)2+2

Patrick: Świetna strona, ratuje z opresji o wiele lepiej, niż sterty podręczników

jola: y=2x²−4x+1

jola: y=2x²−4x+1 przedstaw w postaci kanonicznej trójmian kwadratowy

jola: f(t)=½t²−2t+1 oblicz miejsca zerowe funkcji proszę o pomoc w rozwiązaniu tych zadań

Gustlik: Proponuję podać tutaj sposób rozkładu na czynniki trójmianów kwadratowych z dwiema zmiennymi typu ax²+bxy+cy². Rozważmy "zwykły" trójmian kwadratowy ax²+bx+c. Za pomocą delty i x₁ i x₂ mozna rozłożyć go na czynniki liniowe a(x−x₁)(x−x₂). Sprowadźmy go z powrotem do postaci ogólnej: a(x−x₁)(x−x₂)=a(x²−x₂x−x₁x+x₁x₂)=ax²−ax₂x−ax₁x+ax₁x₂= =ax²−a(x₂+x₁)x+ax₁x₂ Rozważmy teraz trójmian dwóch zmiennych: a(x−x₁y)(x−x₂y)=a(x²−x₂xy−x₁xy+x₁x₂y²)=ax²−ax₂xy−ax₁xy+ax₁x₂y²= =ax²−a(x₂+x₁)xy+ax₁x₂y² Porównajmy te oba trójmiany: widać, że mają one te same współczynniki liczbowe, dochodzi tylko druga zmienna y. Z tego wynika, ze trójmiany takie mogę rozkładać pomocniczo za pomocą zwykłego trójmianu kwadratowego. Np: Rozłożę na czynniki x²+5xy+6y² Tworzę "zwykły" trójmian kwadratowy o tych samych wspołczynnikach ale z JEDNĄ zmienna x i rozkładam go na czynniki w standardowy sposób: x²+5x+6 Δ=5²−4*1*6=25−24=1 √Δ=1

	−5−1
x1=		=−3
	2

	−5+1
x2=		=−2
	2

Odp: x²+5x+6=(x+3)(x+2) A więc w trójmianie dwóch zmiennych w rozkładzie tylko dopiszemy "y" na końcu. Odp: x²+5xy+6y²=(x+3y)(x+2y)

edudamarek: http://matfiz24.pl Jeśli ktoś ma nadal problemy z pojęciem funkcji, funkcji kwadratowej to zapraszam Cie do niebieskiego linku powyżej, gdzie w formie VIDEO dowiesz się więcej o funkcji w postaci ciekawego i prostego wytłumaczenia. Pozdrawiam.

Dexter: x² + 3x − 18 + 4√x²+3x−6= 0 ODP −5 , 2

Dexteriooo: x2 + 3x − 18 + 4√x2+3x−6= 0 ODP −5 , 2

Dominika: http://zs5.lublin.pl/files/mjaworska/Zadania_przygotowawcze_f_kwadratowa.pdf zrobiłby ktoś 6,7,8 z funkcji kwadratowej?

Emil: Mam problem z zadaniem: Funkcja h jest funkcją postaci h(x) = ax² + bx + c. Wyznacz współczynniki a, b, c jeśli: h(1) = 5 h(3) = 1 1 jest najmniejszą wartością tej funkcji. Proszę o pomoc w postaci komentarza bądź e−mail: MegaManAxess.EL@gmail.com

Marek: Witam, panie Jakubie Grzegorzek − jesteś lepszy od mojego nauczyciela. Wszystko tu jest przejrzyste i zrobione krok po kroku. Dzięki, że zrobiłeś tą stronę − wszystkim się ona przyda. Bardzo ułatwia mi życie na matmie.

Paweł: Czesc Mam prosbe. Mógłbyś wejsc na swoje kont na YT i przeczytac pw odemnie ? chodzi mi o mozliwosc przegladania twoich stron na moim komputerze , na ktorym nie ma internetu. (wiecej w wiadomosci wyjasnilem ) nick na YT to zakaznarzekania z góry dziekuje Paweł

bartek1: https://www.transferbigfiles.com/459f127f-faf0-4871-972c-c4ab6018a42f?rid=yhbbMgeYr6HovdA0Q6P2EQ2 DOBRZE ROZWIĄZANE ? POMOCY LUDZIE :C

PIRAT_PL: Dzięki bardzo jutro mam Pracę klasową która zależy od mojej promocji do 2 technikum, teraz dzięki takim objaśnieniom jestem pewien że moja ocena będzie minimalnie 2 i tylko w górę

LO: Hej mam prośbę czy mógłby mi ktoś pomóc przy tym zadaniu? 1. Rozwiąż układ równań oraz układ nierówności:

	⎧	x2 − 5x − y = −6
a)	⎩	x − y = −1

	⎧	x2 − 8x + 12 < 0
b)	⎩	x2 − x > x2 + 1

Miguel: są gdzieś objaśnienia jak rozwiązywać równania trzeciego stopnia

Jakub: Zobacz na stronę 1691.

Damian: Naszkicuj wykres funkcji y=| sin x|. Pomóżcie.

Jakub: Na stronie 2334 masz jak narysować wartość bezwzględną wykresu.

Seba: Witam, mam takie zadanie obliczyć pole ograniczone wykresami funkcji y=−x² y=x−2 mógłby mi ktoś pomóc starałem sie wzorować na tych zadaniach które się tu pojawiają ale nie mogę tego zrozumieć z góry dziękuje za pomoc

olju: πππππΔ∞≤→⇒≈≈≈≈

Gustlik: Mam fajny sposób na rozkład trójmianów kwadratowych dwóch zmiennych postaci ax²+bxy+cy²: Można łatwo wykazać, że jak wymnożymy dwa dwumiany liniowe jednej zmiennej, np.: (Ax+B)(Cx+D) oraz dwumiany liniowe dwóch zmiennych o tych samych wspólczynnikach liczbowych (Ax+By)(Cx+Dy), to otrzymamy w pierwszym przypadku znany nam dobrze trójmian kwadratowy jednej zmiennej postaci ax²+bx+c, a w drugim − trójmian dwóch zmiennych postaci ax²+bxy+cy². Oba te trójmiany BĘDĄ MIAŁY TE SAME WSPÓŁCZYNNIKI LICZBOWE ! Zatem w rozkładzie tego typu trójmianów dwóch zmiennych mozna sobie pomóc ZWYKŁĄ DELTĄ ! Np. rozłóżmy trójmian x²+5xy+6y na czynniki: Rozkładam pomocniczo trójmian jednej zmiennej o tych samych współczynnikach liczbowych klasycznie za pomocą delty: x²+5x+6=(x+3)(x+2) Δ=5²−4*1*6=1, √Δ=1

	−b−√Δ		−5−1
x1=		=		=−3
	2a		2*1

	−b+√Δ		−5+1
x2=		=		=−2
	2a		2*1

Zatem x²+5xy+6y⁼(x+3y)(x+2y) − dojdą tylko "y". W podobny sposób można rozkładać wielomiany dwóch zmiennych wyższych stopni, jeżeli ich jednomiany składowe mają równe stopnie, tj. sumy potęg x i y, czyli potęgi rozłożone "symetrycznie". Zastąpić je wielomianem jednej zmiennej o tych samych współczynnikach liczbowych, rozłożyć którąś z klasycznych metod, np. grupowaniem, wyłączaniem czynników, wzorami skróconego mnożenia, czy twierdzeniem Bezouta i schematem Hornera lub dzieleniem, a potem w rozkładzie dopisać "y" do wyrazów wolnych. Jeżeli otrzymamy nierozkładalny trójmian kwadratowy ax²+bx+c (Δ<0), to w rozkładzie wielomianu dwóch zmiennych ten trójmian będzie wyglądał tak: ax²+bxy+cy² . Będzie miał te same współczynniki liczbowe oraz zmienną "y".

Gustlik: Ma byc oczywiście x²+5xy+6y², zapomniałem dopisać kwadratu.

Antonio: Czy może ktoś mi wytłumaczyć skąd się wzięła delta. Nie mogę zrozumieć delty b² − 4ac

Jakub: Na stronie 3393 masz wyprowadzenie wzorów na deltę i pierwiastki równania kwadratowego.

Kacper: Wielki szacunek dla człowieka, bądź ludzi, którzy tworzą tą stronę. Naprawde kawał dobrej roboty

Paranoja: Ta strona już nie raz uratowała mi d..., więc bardzo dziękuję za wysiłek włożony w stworzenie jej

Agata: Dla jakich wartości parametru m równanie ma dwa różne rozwiązania? a) x²−6x−5m=0

Jakub: Zadania pisz na forum zadankowym.

Ja123: Mam pytanie, czy owe zadane jest na poziom podstawowy?

	x2 − 5
f(x)=
	√|x − 2| (2x + 6)2

Jakub: Pięknie zapisany wzór funkcji, tylko co z nią trzeba zrobić? Nie podałeś pełnej treści zadania. Nie sądzę jednak, aby to było zadanie na poziomie podstawowym, ponieważ wycofano z tego poziomu zadania z wartością bezwzględną.