rafał: nie bardzo to rozumiem. jeżeli chcielbysmy narysowac to na osi to jakby to wygladało. mam
nadzieje ze takiego przykladu nie bedzie jutro na maturze.
4 maj 16:59
Jakub: Rozwiązaniem są wszystkie liczby rzeczywiste, dlatego nie zrobiłem rysunku. Co miałbym na nim
zaznaczyć? Cały oś liczbową? Nic to nie ułatwi zrozumienie rozwiązania.
4 maj 17:37
ADAM: a czy tu nie powinno być żadnego rozwiązania, bo przecież odległość nie możr równać się liczbie
ujemnej?
2 lis 14:16
uczony dziadek: Podane rozwiązanie nie jest prawidłowe.
Właściwa odpowiedż to: liczba X jest w zbiorze niedomkniętym od −15 do 3.
18 sty 13:57
Malapaula: x należy do (−15,3)
1 lut 19:50
Miquel: −uczony dziadek: wg. Twojej teorii −15 juz nie nalezy do zbioru, na udowodnienie rozwiaz
roznanie:
|x+6|>−9 liczymy dla x=−15
|−15+6|>−9
|−10|>−9
odp: Wartosc bezwzgledna liczby −10 wynosi 10, oznacza to, ze jest wieksza od −9
18 kwi 16:52
przyszly odkrywca: Mam podobne myśli jak Adam, przecież nie może być rozwiązania skoro liczba jest ujemna i jak
mam to rozumieć, że dlatego rozwiązania są wszystkie liczby rzeczywisty?
Czy −9>−9 jest prawda?
7 maj 14:50
Dżoli: też by m prosiła o bardziej dokładne wyjaśnienie tego przykładu..

26 lut 23:04
Dżoli: chyba już wiem o co chodzi z tym zadaniem. przyszly odkrywca −−> napisałeś czy −9>9, źle
rozumiesz to zadanie, ponieważ to zadanie wygląda tak : Ix + 6I > −9, rozwiązaniem są
wszystkie liczby rzeczywiste, a więc każdą dowolną liczbę podstawiamy za x. Gdy podstawimy
jakąkolwiek liczbę, nawet ujemną to wynik z wartości bezwzględnej wyjdzie nam dodatni także
będzie większy od −9. przyszly odkrywca −−> jak byś podstawił liczbę taką aby w wartości
bezwzględnej wyszło −9 to "opuszczając wartość bezwzględną otzymamy 9, czyli liczbę wiekszą od
−9, popatrz:
I −15+6 I > −9
I −9 I > −9
9 > −9
27 lut 16:10
Jakub: Dokładnie o to chodzi Dżoli.
28 lut 00:54
kkkasiula: mi też wyszło(−15,3) ale myślmy co tu źle..

31 mar 19:36
kkkasiula: juz wiem −15 nie nalezy do przedziału i 3 równiez dlatego liczby R
31 mar 19:37
Rafał: Małe pytanie. Mój nauczyciel uczył nas innego sposobu rozwiązywania nierówności. Mianowicie:
|x+6|>−9 rozbijamy to na 2 przypadki z alternatywą zdań:
x+6>−9 lub x+6<9
x>−15 lub x<3
I teraz pora na pytania. Wartość logiczna alternatywy jest prawdziwa gdy jedno ze zdań jest
prawdziwe. Ale skąd twierdzenia logiczne biorą się w tej wartości bezwzględnej? Trzeba to
poprostu zapamiętać czy jest jakaś zasada?
13 lut 12:40
Jakub: Nierówność |x+6| > −9 należało rozwiązać korzystając z interpretacji geometrycznej wartości
bezwzględnej. Na stronie
1653 masz wiele nierówności rozwiązanych sposobem Twojego
nauczyciela.
Jednak przykład |x+6| > −9 dużo prościej rozwiązać nie sposobem Twojego nauczyciela tylko po
prostu z samego zrozumienia, co to jest wartość bezwzględna. Wartość bezwzględna z dowolnej
liczby jest zawsze dodatnia lub równa zero. Na stronie
3554 i
15 masz więcej o tym.
Jak patrzysz na nierówność |x+6| > −9, to po lewej stronie masz wartość bezwzględną i oczywiste
jest, że ona jest zawsze większa od −9, jeżeli jest dodatnia lub równa zero. Z tego wynika, że
|x+6| zawsze będzie większe od −9 i rozwiązaniem tej nierówności jest zbiór wszystkich liczb
rzeczywistych.
Inny przykład
|x+6| > 5
x+6 > 5 lub x+6 < −5
Wynika to z tego, wartość bezwzględna jest większa od 5, gdy wartość bezwzględna jest z liczb
większych od 5 lub mniejszych od −5 np.
|6| > 5, |−6| > 5, |10| > 5, |−12| > 5
Czyli x+6 musi spełniać albo ten warunek x+6 > 5, albo ten warunek x+6 < −5, aby |x+6| >5.
Oczywiście nie może być spójnika ,,i'', ponieważ jednocześnie x+6 nie może być większa od 5 i
mniejsza od −5. Nie ma po prostu takich liczb, które jednocześnie by spełniały obydwa warunki.
13 lut 15:03
Rafał: Znam definicje wartości bezwzględnej

Przygotowuję się do matury rozszerzonej i rozwiązując
zadanka zastanawiałem się czemu jest tak a nie inaczej. Po prostu zostałem nauczony tak trochę
bezmyślnie to robić, a nie rozumieć. Co do spójnika "i" to oczywiście, że nie może tam
występować

Weźmy przykład z odwróconym znakiem większości.
|x+6|<−9 rozbijamy na koniunkcję zdań :
x+6<−9 i x+6>9
x<−15 i x>3
Jeżeli się nie mylę, aby całość przyjmowała wartość "prawda" to oba wyrażenia muszą być
prawdziwe. W tym więc przypadku mamy fałsz i równanie nie ma rozwiązania. Zgadza się?
13 lut 21:04
Jakub: Racja. Nie ma liczb spełniających jednocześnie nierówności x <−15 i x>3 i dlatego piszesz |x+6|
< −9 nie ma rozwiązania.
Tylko ja bym nie próbował nawet rozbijać na te dwie nierówności. Jakbym zobaczył nierówność
|x+6| < −9 to bym napisał. Wartość bezwzględna nie może być ujemna, więc ta nierówność nie ma
rozwiązania. Od razu, bez tego schematycznego rozwiązania.
Podobnie:
|x+6| > −10
Wartość bezwzględna jest zawsze dodatnia lub równa zero, więc tą nierówność spełniają wszystkie
liczby rzeczywiste.
Oczywiście, jak po prawej stronie nierówności jest jakaś liczba dodatnia, to rozwiązanie
schematyczne jest najszybsze.
Inna sprawa, czy rozumiesz dlaczego to rozwiązanie schematyczne wygląda jak wygląda. Próbowałem
to wyjaśnić w poprzednim wpisie, ale nie wiem, czy jasno to opisałem.
14 lut 00:47
Rafał: Rozumiem

Zaznaczenie na osi, sprawdzenie rozwiązania według definicji. Dziękuję za pomoc

PS Bardzo fajna stronka jeżeli chodzi o przygotowanie do matury, ale zadania chyba w większości
są za proste

14 lut 19:56
aaa:
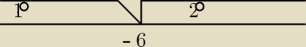
JA to wyjasnie w miare prosty sposob:
|x+6|>−9
x+6=0
x=−6
1
o:
x∊(−
∞,−6)
−x−6>−9
x<3
czesc wspolna x∊(−
∞,−6) i x<3 wynosi : x∊(−
∞,−6)
2
o:
x∊<−6,
∞)
x+6>−9
x>−3
czesc wspolna x∊<−6,
∞) i x>−3 wynosi : x∊<−6,
∞)
suma wynikow x∊(−
∞,−6) i x∊<−6,
∞) wynosi R −wszystkie liczby rzeczywiste
6 maj 02:39
Jakub: Mały błąd w 2o
x+6 > −9
x > −9−6
x > −15
cześć wspólna x∊<−6,∞) i x > −15 wynosi: x∊<−6,∞)
dalej ok.
6 maj 14:30


 Przygotowuję się do matury rozszerzonej i rozwiązując
zadanka zastanawiałem się czemu jest tak a nie inaczej. Po prostu zostałem nauczony tak trochę
bezmyślnie to robić, a nie rozumieć. Co do spójnika "i" to oczywiście, że nie może tam
występować
Przygotowuję się do matury rozszerzonej i rozwiązując
zadanka zastanawiałem się czemu jest tak a nie inaczej. Po prostu zostałem nauczony tak trochę
bezmyślnie to robić, a nie rozumieć. Co do spójnika "i" to oczywiście, że nie może tam
występować  Weźmy przykład z odwróconym znakiem większości.
|x+6|<−9 rozbijamy na koniunkcję zdań :
x+6<−9 i x+6>9
x<−15 i x>3
Jeżeli się nie mylę, aby całość przyjmowała wartość "prawda" to oba wyrażenia muszą być
prawdziwe. W tym więc przypadku mamy fałsz i równanie nie ma rozwiązania. Zgadza się?
Weźmy przykład z odwróconym znakiem większości.
|x+6|<−9 rozbijamy na koniunkcję zdań :
x+6<−9 i x+6>9
x<−15 i x>3
Jeżeli się nie mylę, aby całość przyjmowała wartość "prawda" to oba wyrażenia muszą być
prawdziwe. W tym więc przypadku mamy fałsz i równanie nie ma rozwiązania. Zgadza się?
 Zaznaczenie na osi, sprawdzenie rozwiązania według definicji. Dziękuję za pomoc
Zaznaczenie na osi, sprawdzenie rozwiązania według definicji. Dziękuję za pomoc  PS Bardzo fajna stronka jeżeli chodzi o przygotowanie do matury, ale zadania chyba w większości
są za proste
PS Bardzo fajna stronka jeżeli chodzi o przygotowanie do matury, ale zadania chyba w większości
są za proste 
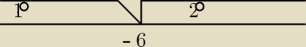 JA to wyjasnie w miare prosty sposob:
|x+6|>−9
x+6=0
x=−6
1o:
x∊(−∞,−6)
−x−6>−9
x<3
czesc wspolna x∊(−∞,−6) i x<3 wynosi : x∊(−∞,−6)
2o:
x∊<−6,∞)
x+6>−9
x>−3
czesc wspolna x∊<−6,∞) i x>−3 wynosi : x∊<−6,∞)
suma wynikow x∊(−∞,−6) i x∊<−6,∞) wynosi R −wszystkie liczby rzeczywiste
JA to wyjasnie w miare prosty sposob:
|x+6|>−9
x+6=0
x=−6
1o:
x∊(−∞,−6)
−x−6>−9
x<3
czesc wspolna x∊(−∞,−6) i x<3 wynosi : x∊(−∞,−6)
2o:
x∊<−6,∞)
x+6>−9
x>−3
czesc wspolna x∊<−6,∞) i x>−3 wynosi : x∊<−6,∞)
suma wynikow x∊(−∞,−6) i x∊<−6,∞) wynosi R −wszystkie liczby rzeczywiste