PROblem
TOmek:
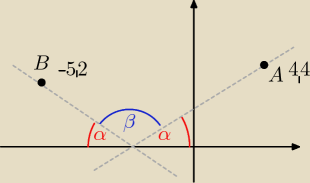
Na płaszczyźnie z układem współrzędnych dane sa punkty A i B oraz proste k i l tworzące z
prostą o równaniu y=0 kąty o równych miarach(patrz rysunek).
a) wyznacz równania prostych k i l
b)Oblicz tangens kąta β
A=(4,4)
B=(−5,2)
9 lip 19:46
9 lip 20:01
TOmek: czas, ucieka matura tuż, tuż, nie ma miejsca na zastuj...

9 lip 20:07
TOmek: nadal nie wiem jak to zrobić...
9 lip 20:11
rumpek:
Zrobię a) na szybko bo coś za mocno "pioruny walą" koło mojego bloczku

No to tak:
Masz proste "k i l". Prosta k załóżmy, że jest rosnąca, czyli jej a > 0 (a) i przechodzi przez
punkt A(4,4). Prostą "l" załóżmy, że jest malejąca czyli a<0 (−a) i przechodzi przez punkt
B(−5,2).
Kluczowym w tym zadaniu jest wykorzystanie wiedzy z:
https://matematykaszkolna.pl/strona/1212.html.
Wpierw jednak oznaczmy sobie jakoś
równania tych prostych: Prostą "k" jako np.: y = ax + b, natomiast prostą "l" jako: y = a'x +
b'. Korzystając z tego linka wyżej mamy: a = tgα (to wiadome). Natomiast dla prostej "l − tej
malejącej" mamy tg(180
o − α) [naprawdę to na rysunku te kąty to:
β + α]. Dobra to teraz czas na wzory redukcyjne tg(180
o − α) = −tgα = −a. Czyli a' = −a.
Kolejna obserwacja kluczowa to to, że mają wspólne miejsce zerowe. Czyli mamy:
| ⎧ | axo + b = 0 | |
| ⎩ | −a'xo + b' = 0 |
|
Podstawiając jedno pod drugie mam:
ax
o + b = −a'x
o + b'
Zamieniam stronami:
2ax
o = b' − b / : 2
To teraz pozostało podstawić to x
o do (ax
o + b = 0 albo −a'x + b' = 0) więc:
b' − b + 2b = 0
b' + b = 0
b' = −b
Mamy kolejną przydatną informację, że b' = −b czyli mamy równania prostych:
k: y = ax + b
l: y = −ax − b
Podstawiasz pod punkty i mam rozwiązanie

9 lip 20:17
rumpek: mamy*, matura tuż tuż? Jakie ty już działy zrobiłeś?
9 lip 20:19
TOmek: o kurcze, dziekuje

9 lip 20:19
TOmek: wszystkie, teraz sie biore za trudniejsze zadania.
9 lip 20:20
rumpek:
Wszystkie? Czyli stereometria, prawdopodobieństwo

?
Trudniejsze zadania?
Jakim ty systemem jedziesz

?
9 lip 20:21
TOmek: Ja za matme wziąłem się prawie rok temu, wszystkie działy mam ogarniete na nawet niezłym
poziomie,( prawdopodobieństwo i logarytmy troche mniej), Jedynie prawdopodobieństwo cięzko mi
weszło do głowy(ale jak robiłem zadanie z najnowszej matury to wyszło mi dobrze)
Nie chce być jakimś 'koksem' z matmy, co robi każde zadania, ja chce tylko mieć jak najwiecej
procent z matury rozszerzonej.

9 lip 20:27
rumpek: No zadań takich jak w kiełbasie w ogóle nie dają, jedynie ze stereometrii czasami.
Tak się składa, że mam "kiełbasy książkę" i tam jest inny rysunek niż twój

I nawet proste są
podpisane, więc będziesz musiał zmienić trochę oznaczeń

9 lip 20:31
ICSP: ja bez praktycznie bez nauki z rozszerzonej miałem 80% więc nie musisz wcale robić zadań żeby
mieć dużo procent z rozszerzenia.
9 lip 20:32
ICSP: a która to część Kiełbasy?
9 lip 20:32
rumpek: "zielona"

czyli druga

9 lip 20:34
ICSP: a która strona jeśli można spytać

9 lip 20:35
ICSP: 58?
9 lip 20:35
rumpek:
Oznaczenia do tego poprawionego to:
k: y = ax + b
l: y = a'x + b'
tgα = a
a' = −a
czyli:
k: y = ax + b
l: y = −ax − b
Pod y = ax + b podstawiasz A(−5,2)
Pod y = −ax − b podstawiasz B(4,4)
9 lip 20:37
TOmek: no ale ja nie jestem, jakims wielkim talentem matematycznym, więc musze porządnie, sumiennie
pracować..

Co do ksiązki kiełbasy, nie zgadzam sie z Tobą. Jest to jedna z nielicznych
ksiązek, która jest sprawdzona przez wielkie grono osób, które pozytywnie sie o niej
wypowiadali. Moj kumpel przygotowywał sie tyko na kiełbasie i napisał swietnie maturke

9 lip 20:37
rumpek: Tak

9 lip 20:37
TOmek: tak 58
9 lip 20:37
rumpek: Oficyny są dobre

Poza tym na razie nie robię w ogóle zadań, tylko przeglądam te forum

Coś myślę, że tak do końca lipca będę umiał dość dobrze kombinatorykę, a do września
stereometrie. Za prawdopodobieństwo wezmę się we wrześniu i idę na maturkę

9 lip 20:39
TOmek: każdy ma swoj plan.

9 lip 20:42
ICSP: więc Tomku prosze oto zadanko dla ciebie:
Oblicz wartość wyrażenia:
sin10o * cos20o * cos40o
Pamiętaj aby nie pominąć żadnego toku rozumowania gdyż może to skutkować odjęciem punktów.
9 lip 20:44
rumpek:
TOmek to masz tak dla powtórki:
Wiedząc, że trójkąt równoramienny ABC gdzie boki AC oraz BC są sobie równe, a ponadto miara
kąta ∡ACB wynosi 2 alfa. Promień okręgu wpisanego w ten trójkąt równoramienny ma długość r.
Oblicz długość boków ABC.
Banalne zadanko

9 lip 20:45
ICSP: wiem że banalne ale tak na rozgrzewkę mu dałem.
9 lip 20:47
rumpek: Że banalne to mówiłem − pisałem o swoim

9 lip 20:48
TOmek: sin10 * cos20 * cos40
jakaś podpowiedź?
9 lip 20:55
ICSP: nie ma podpowiedzi

Sam musisz wpaść na rozwiązanie. Wtedy gwarantuje ci że zapamiętasz sposób
robienia takich zadań do końca życia.
9 lip 20:59
rumpek: ICSP chyba zrobiłem, i podpowiedź dla
TOmka (nie wiem czy dobra) to wykorzystałem
| | 1 | |
sin2α = 2sinαcosα, a wynik |
| nie wiem czy dobry |
| | 8 | |
9 lip 21:00
rumpek: Dobra uciekam bo coraz mocniej "błyskawice dają"


9 lip 21:01
ICSP: | | 1 | |
brawo rumpku  Odp. |
| jest poprawną odpowiedzią. |
| | 8 | |
9 lip 21:04
ICSP: Ja też uciekam. Muszę jeszcze dziś przejść minimum jedną misję. Będę później.
9 lip 21:05
TOmek:
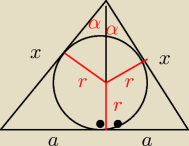
dobra to pierw zajme sie zadanie rumpka:
troche mi obrazek nie wyszedł
| | 2P | | x2*sin2α | |
r= |
| = |
| = |
| | a+b+c | | 2x+2a | |
sinα*x=a
| x2*sin2α | |
| =r wyznaczamy "x" dobrze? |
| 2x+2(sinα*x) | |
9 lip 21:08
9 lip 21:13
TOmek: cwaniak

ale na oko dobrze jest?
9 lip 21:18
rumpek:
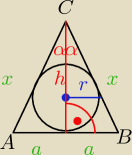
Kiedyś je robiłeś powinieneś pamiętać. Ja zrobiłbym sposobem całkiem innym:
No i teraz patrzę na h i x, chcę te oznaczenia otrzymać więc:
Wzory które wykorzystam to:
Łatwo zauważyć, że ten drugi wzór ma w mianowniku obwód który mogę oznaczyć literką p.
rp = 2P / : 2
Więc tylko przyrównam te pola
| | a | | a | |
(a + |
| ) * r = a * |
| |
| | cosα | | tgα | |
| | 1 | | a2 | |
(1 + |
| ) * r * a = |
| / : 2 |
| | cosα | | tgα | |
| | 1 | | a | |
r * (1 + |
| ) = |
| / * tgα |
| | cosα | | tgα | |
| | 1 | |
a = tgα * r * (1 + |
| ) |
| | cosα | |
Jak mam "a" to mogę zdziałać cuda jednak tych cudów nie chce mi się pisać i podam tylko
odpowiedzi

No i mam takie odpowiedzi no i błędu u siebie nie widzę

Jednakże, Kiełbasa jak to bywa podaje inne odpowiedzi

np.:
Podstawa:
Ramię:
Ale on tu wykorzystał dwusieczne, nie wiem po co ale luz

Także myślę, że błędu nie popełniłem

a kiełbasa to kiełbasa

zawsze jakieś trudniejsze
sposoby znajdzie

9 lip 21:43
TOmek: 
9 lip 21:57
ICSP: Hodzio jak wróci to zapewne się tym zadaniem zainteresuje. On lubi właśnie takie działanie na
literkach a nie na liczbach.
9 lip 21:58
ICSP: Godzio oczywiście.
9 lip 21:59
ICSP: To może coś takiego:
W trapez równoramienny wpisano okrąg. Oblicz obwód i pole trapezu jeśli jego kąt ostry ma miarę
60o a promień okręgu opisanego na tym trapezie jest równy 1cm.
9 lip 22:04
rumpek:
ICSP dla mnie to zadanie?

Jak dla mnie to zrobię je jutro, bo zaraz szykuję się do
spania, bo o 5 trzeba wstać

.
Zadanie nie wydaje się trudne, skorzystałbym przede wszystkim z :
https://matematykaszkolna.pl/strona/874.html
Pierwsza zależność, no i oczywiście jakieś tam zależności sinusów cosinusów itp.

Ale to
trzeba zadanie zrobić

9 lip 22:11
ICSP: Zadanie dla Tomka

Przecież to jego temat

Niech ma troszkę trudniejsze zadania.
9 lip 22:12
Vax: ICSP ten promień na pewno odnosi się do okręgu opisanego, a nie wpisanego ?

9 lip 22:19
Vax: edit// A ok, może być i tak

9 lip 22:21
ICSP: na pewno

9 lip 22:25
TOmek:
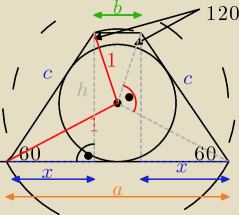
wiem ,zajebisty obrazek

180−60=120
1
2+1
2=c
2
c=
√2
cos60*c=x
sin60*c=h
teraz korzystamy z takiej zaleznosci
https://matematykaszkolna.pl/strona/874.html
układ równań
b+a=2c
b+a=2
√2⇒a=2
√2−b
| √2 | | a−b | |
| = |
| /*2 ⇒√2=2√2−b−b⇒ 2b=−√2+2√2 |
| 2 | | 2 | |
2b=
√2
liczę teraz "a"
2a=3
√2
czyli mam dane liczę obw.
c=
√2
| | 3√2 | | √2 | |
Obw= |
| +2*√2+ |
| =4√2 |
| | 2 | | 2 | |
jaki masz tam wyniki

10 lip 12:26
TOmek:
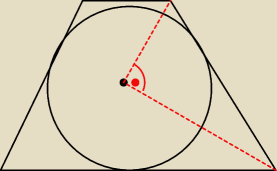
i odrazu mam pytanie, bo znam taką zależność ,ze jak okrąg jest wpisany w czworokąt to trójkąt
(ten na obrazku) jest prostokątny, lecz jak to udowodnić

10 lip 12:28
ICSP: między czerwonymi prostymi nie ma kąta prostego

10 lip 12:29
TOmek: what?

10 lip 12:33
ICSP: całe rozumowanie źle

.
10 lip 12:34
ICSP:
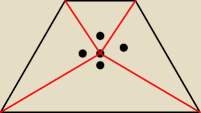
według ciebie zależności w takim trapezie wyglądają następująco. Teraz pytanie do ciebie: Ile
będą miały kąty przy podstawie oraz przy wierzchołku skoro czerwone odcinki są identyczne?
10 lip 12:36
TOmek: pamietam ,ze kiedyś pytałem sie kogoś z górnej półki i mi przytaknął ,ze tak zawsze jest,
albo pomyliłem to z czymś innym.. znasz jakies podobne twierdzenie?
P.S zaraz zrobie od początku te zadanie, ale pierw chce to wytłumaczyć
10 lip 12:37
ICSP: możliwe że to twierdzenie jest prawdziwe dla trapezu nierównoramiennego ale pewien nie jestem.
Osobiście stawiałbym na trapez prostokątny.
10 lip 12:40
TOmek:
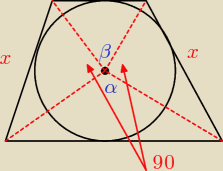
180+α+β=360
10 lip 12:40
ICSP: α i β − kąty wierzchołkowe. Czyli są sobie równe co znaczy że mają po 90o. Czyli ta figura to
kwadrat.
10 lip 12:42
TOmek: myśle,ze masz racje,iz ta zalezność którą podałem występuje tylko w trapiezie prostokątnym.
10 lip 12:45
ICSP: ktoś to najwyżej potwierdzi później

Ty masz chyba fajne zadanko do rozwiązania

10 lip 12:47
TOmek: zaraz będę robił, na nowo

10 lip 12:47
TOmek:
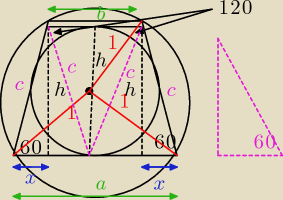
180−60=120
o
wiemy ,że
a+b=2c
| | x | | 1 | | 1 | |
cos60= |
| ⇒ |
| *c=x ⇒ x= |
| *c |
| | c | | 2 | | 2 | |
Z zależnosci trójkątów 30,60,90 mamy
2c=x
h=x
√3
−−−−−−−−−−−−−−−−−−−−−−−−−−
−−−−−−−−−−−−−−−−−−−−−−
h=x
√3
−−−−−−−−−−−−−−−−
2x=a−b
a+b=2c /wiemy ,ze 2c=x
2x=a−b
a+b=x
potrzebuje wskazówki..
10 lip 13:26
TOmek: | | 1 | |
wiemy jeszcze ,ze |
| h=r(promien okregu wpisanego) |
| | 2 | |
| | 2P | |
r= |
| P− pole czworokąta |
| | 2c+a+b | |
teraz moge to wykorzystac

10 lip 13:31
TOmek: czekajcie mam pomysł, zobaczymy co z tego wyjdzie, jak znacie łatwiejsze sposoby pisac

10 lip 13:32
TOmek: dupa...
10 lip 13:34
rumpek:
Mi tam wynik wyszedł jakiś. W mianowniku coś z 7 a w liczniku pamiętam, że chyba coś z
√21
było

ale to dzisiaj o 6 robiłem

także mogłem coś pokręcić, a wyniku nie zapisałem

10 lip 13:36
TOmek: trudne zadanko.. jak na razie wypisałem tylko wszystkie dane, najgorsze ,ze zadnego układu
równań nie mogę ukrecic, by wreszcie cos wyszło na czysto

10 lip 13:37
rumpek:
na co ci układ równań?
Jak robiłem rano to na pewno wykorzystałem twierdzenie cosiunusów, i o tym co pisałem wyżej z
zależności: 2c = a + b itp.. sin60o oraz cos60o ...
10 lip 13:39
TOmek: c=a−b
a+b=2c
wychodzi z tego ,ze
c=2b
czyli ramie "c" jest 2 razy krótsze od podstawy 'b'

10 lip 13:41
TOmek: racja, przeciez tw. cosinusów i zadanie rozwiązane.. tylko juz nie mam siły liczyc ..
10 lip 13:41
rumpek: no nie tylko twierdzenie cosiunusów ... tylko coś jeszcze ...Zadanie jest dość proste
10 lip 13:47
TOmek: banalne jest przeciez
10 lip 13:49
rumpek: Skoro takie banalne to mogłeś zrobić je dobrze za pierwszym podejściem

a tu trzy próby i
zero pomysłu z "Twojej strony" ...
10 lip 13:51
TOmek: smieszy mnie te Twoje "banalne jest" , 'łatwe to jest', fajnie ,ze jestes dobry z matmy, ale to
nie znaczy ,ze musisz sie wywyszać. Bierz przykład z Ety, Jacka, Godzia oni motywują do pracy,
Ty przeciwnie, upokazasz.
Koniec
10 lip 13:53
rumpek: 
że banalne to ty napisałeś... Ja odpowiedziałem − skoro takie łatwe to czemu nie
rozwiązałeś?
10 lip 13:55
Vax:
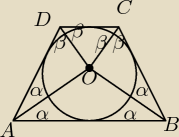 ICSP
ICSP Wracając do tego co napisał
TOmek z kątem prostym w trapezie równoramiennym, to
ma on racje, zauważ, że w trapezie równoramiennym kąty przy tej samej podstawie są równej
długości, dodatkowo środek okręgu wpisanego wyznaczony jest oczywiście przez dwusieczne kątów
czworokąta, teraz korzystając z tego, że suma miar kątów w czworokącie wynosi 360* mamy:
4α+4β = 360 /:4 ⇔ α+β = 90* czyli istotnie kąt DOA = kąt BOC = 180−(α+β) = 90*

Pozdrawiam.
10 lip 13:56
Vax: Oczywiście kąty są tej samej miary, a nie długości, literówka

10 lip 13:57
TOmek: tylko własnie nie wiem, czy ten pierwszy wynik jest dobry. Dobrze by było, gdyby ICSP podał by,
bym mógł sprawdzić
10 lip 13:58
rumpek:
 TOmek
TOmek a powiem ci tyle, że wcale nie jestem dobry z matmy, mam jeszcze większe problemy
niż ty

10 lip 13:58
ICSP: Pierwszy wynik jest zły.
10 lip 14:09
ICSP: Vax przez dwusieczne, tu moje pytanie czy promień okrągu opisanego jest dwusieczną kąta?
10 lip 14:11
rumpek: ICSP wynik to jakiś taki z 7 w mianowniku i chyba
√21 gdzieś tam? Bo nie pamiętam już
dokładnego

10 lip 14:11
TOmek: Vax czyli w trapezie prostokątnym ,gdzie jest wpisany okrag, to takze występuje trójkąt
prostokątny?
10 lip 14:15
Vax: ICSP, nie rozumiem pytania, promień okręgu wpisanego w trapez jest odległością środka okręgu
(wyznaczonego przez punkt przecięcia dwusiecznych kątów danego trapezu) od dowolnego boku,
dodatkowo próbując przekonać TOmka, że nie ma racji, napisałeś, że kąty AOB i COD są
wierzchołkowe, stąd by wynikało, że dany trapez musi być kwadratem, ale to nie jest prawda,
przecież punkty A,O,C ani B,O,D nie są współliniowe..
10 lip 14:15
Vax: TOmek tak, w trapezie prostokątnym również w tamtym miejscu występuje kąt prosty co można
dowieść w identyczny sposób

Pozdrawiam.
10 lip 14:16
Vax: Aha, ICSP promień okręgu OPISANEGO na trapezie jest równy odległości środka danego okręgu od
któregoś z wierzchołków, ale zauważ, że środek okręgu wpisanego jest wyznaczony przez
dwusieczne kątów, a środek okręgu opisanego, przez środkowe

10 lip 14:18
ICSP: wiec gdzie jest błąd w rozumowaniu Tomka. Wyliczył długość ramienia z twierdzenia Pitagorasa.
Jednak albo policzył źle(co jest niemożliwe bo sprawdzałem nie raz) albo jest gdzieś właśnie
błąd w rozumowaniu. Ja nie potrafie tego błędu znaleźć.
10 lip 14:19
ICSP: czyli w tym zadaniu tamten kąt nie jest prosty?
10 lip 14:20
Vax: Błąd leży w tym, że
TOmek przyjął środek okręgu wpisanego za środek okręgu opisanego, skąd
całe zamieszanie

10 lip 14:21
Vax: W dowolnym trójkącie prostokątnym jak i równoramiennym tamten kąt jest prosty, czego dowód
pokazałem wcześniej..
10 lip 14:22
Vax: trapezie*
10 lip 14:22
ICSP: to o to chodzi

10 lip 14:22
TOmek:
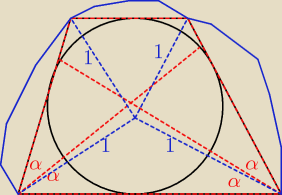
o to chodzi? prawda?

10 lip 14:32
TOmek: skopałem, ten obrazek, juz wiem o co chodzi..
10 lip 14:35
Vax: Środek okręgu opisanego jest wyznaczony przez punt przecięcia symetralnych boków, czyli przez
proste prostopadłe do boku przechodzące przez ich środek

10 lip 14:35
TOmek: dziekuje, wszystko juz jest jasne

10 lip 14:38
ICSP: wszystko oprócz wyniku

10 lip 15:05
TOmek: dokładnie, dobrze by było, zeby jakiś PRO zrobił te zadanko

10 lip 15:10
ICSP: ale to jest zadanie dla ciebie

My chcemy ci pomóc sie rozwinąć. Oczywiście jakiś PRO może
podać odpowiedzi bo jestem pewien że ktoś już to rozwiazał

10 lip 15:33
Vax: | | 8√21 | | 6√3 | |
Jeżeli się nigdzie nie pomyliłem, to L = |
| oraz P = |
| |
| | 7 | | 7 | |
Pozdrawiam.
10 lip 15:59
ICSP: No to masz już poprawne odpowiedzi

Teraz wystarczy że znajdziesz sposób rozwiązania

10 lip 16:00
Jack:
jeszcze to pierwsze zadanie, można je było zrobić np. przez podobieństwo

10 lip 16:51
TOmek:
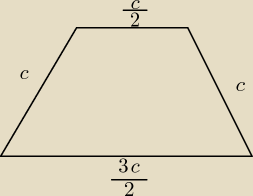
2x=a−b
a+b=2c
| | c | |
//wiemy ,ze |
| =x ⇒2x=c ⇒ |
| | 2 | |
2x=a−b ⇒ c=a−b ⇒ a=c+b
| | c | |
a+b=2c ⇒ c+b+b=2c ⇒ 2b=c ⇒ b= |
| |
| | 2 | |
ramię trapezu jest 2 razy dłuższe od mniejszej podstawy
2x=a−b ⇒ b=−2x+a
| | c | | c | | 3c | |
a+b=2c⇒a−2x+a=4x ⇒ 2a=6x /:2 ⇒ a=3x ⇒(wiemy |
| ) ⇒ a=3* |
| ⇒a= |
| |
| | 2 | | 2 | | 2 | |
−−−−−−−−−−−−−−−
teraz spróbujmy wyrazić x za pomocą "c"
| | 3c | | c | | 2c | |
2x=a−b ⇒ 2x= |
| − |
| = |
| =c |
| | 2 | | 2 | | 2 | |
2x=c (przynajmniej wiem ,ze obliczenia się zgadzają)
−−−−−−−−−−−−−−−−−−−−−−−−−−−−
nie mam pojecia jak te
c obliczyc.... prosze o wskazowki..
10 lip 17:45
TOmek: 
10 lip 18:04
Jack:
Jeśli oprócz danych na rys. nic więcej nie ma, to "c" nie da się wyliczyć. Mogą być przecież
różne trapezy w zależności od "c" − trapezy podobne.
(nie czytałem dokładnie poprzednich wpisów − może o tym trapezie jednak coś więcej wiadomo)
10 lip 19:01
TOmek: Okrąg jest opisanym na trapiezie i promien tego okregu ma 1cm, jednak nie wiem jak uzyc tej
informacji.
10 lip 19:03
ICSP: Oblicz przekątną trapezu x twierdzenia cosinusów. Następnie ułóż trójkąt prostokątny z
przekątną wysokością oraz częścią dłuższej podstawy. Jeśli wszystko dobrze wyliczysz z tego
trójkąta będziesz wstanie wyliczyć c. Później to już łatwizna.
10 lip 19:05
Vax:
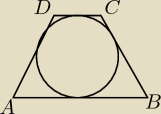
Ja to wyliczyłem zauważając, że promień okręgu opisanego na trójkącie BDC jest równy promieniu
okręgu opisanego na trapezie ABCD

10 lip 19:17
TOmek: d−przekątna trapezu
| | 1 | | 3c | |
d2=a2+c2−2ac |
| // a= |
| |
| | 2 | | 2 | |
d
2=h
2+(a−x)
2
myslisz ,ze z tego dam rade wyliczyc?
10 lip 19:17
TOmek: te zadanie znacznie przewyzsza poziom maturki rozszerzonej ...

10 lip 19:20
ICSP: nie to zadanie jest na poziomie matury rozszerzonej. Jednak widzę ze nie możesz sobie z nim
poradzić:0 Chociaż tamto z udowodnieniem zrobiłeś?
10 lip 20:49
Trivial: Hello.

10 lip 20:58
ICSP: Proszę
Trivial przyszedł

Jedyny temat na forum w którym coś się dzieje. Trivialku nie
znasz przypadkiem jakiejś metody itteracyjnej?
10 lip 20:59
Trivial: Które zadanie rozwiązujecie, bo nie czytałem całego topicu.
10 lip 21:00
ICSP: tzn są dwa nie rozwiązane.
Oblicz:
sin10
o * cos20
o * cos40
o
oraz
W trapez równoramienny wpisano okrąg. Oblicz obwód i pole trapezu jeśli jego kąt ostry ma miarę
60o a promień okręgu opisanego na tym trapezie jest równy 1cm.
Z tym drugim Tomek sobie chyba nie poradził a z pierwszym się mierzy. Jak chcesz możesz zrobić
drugie

10 lip 21:01
Trivial: Widzę, że bez kartki się nie obejdzie tym razem.

10 lip 21:03
ICSP: Trivial, a moje pytanko?
10 lip 21:05
Trivial: Jakie pytanko?

10 lip 21:06
Godzio:
Ten pierwszy to
TOmek kilka razy robił, tak to jest jak się idzie działami po kolei i
zapomina się poprzednie ... Trzeba mieszać

10 lip 21:06
ICSP: "Trivialku nie
znasz przypadkiem jakiejś metody itteracyjnej?"
10 lip 21:08
Trivial: Aha, nie.

Znam tylko iteracyjną metodę pierwiastkowania.
10 lip 21:08
ICSP: Itteracyjna metoda pierwiastkowania? Czego ona dotyczy?
10 lip 21:09
Trivial: Pierwiastkowania.

10 lip 21:11
Trivial: Możesz sobie obliczyć np. przybliżoną wartość √3, itd.
10 lip 21:11
ICSP: yyy nie łatwiej na kalkulatorze?
Jeśli się nie mylę to do tego się używa pochodnych?
10 lip 21:13
Trivial: Nie. Oczywiście, że łatwiej, ale jak się nie ma kalkulatora pod ręką, to można sobie wyliczyć
szybko.
10 lip 21:14
ICSP: To jak to się robi?
10 lip 21:15
Vax: ICSP chodzi o nie korzystanie z kalkulatora, z kalkulatorem nie ma zabawy

Ja osobiście
do tego typu zadań stosuję metodę bisekcji, przystępnie opisali jej działanie na wiki:
http://pl.wikipedia.org/wiki/Metoda_r%C3%B3wnego_podzia%C5%82u
Jeżeli szukamy przybliżenia wartości
√3, to wystarczy zastosować daną metodę dla wielomianu
W(x) = x
2−3, zaczynając np od przedziału [1;2]

Pozdrawiam.
10 lip 21:16
Trivial:
Żeby wyliczyć
√a trzeba kilka razy przeiterować.
Gdzie x
0 zgadujemy (nie ma znaczenia czy trafimy, po kilku iteracjach i tak dostaniemy
poprawną odpowiedź − przybliżenie).
10 lip 21:16
ICSP: nie łapię:(
10 lip 21:19
Trivial:
Przykład.
Będziemy liczyć
√2.
a = 2, x
0 zgadujemy, np. 1.5:
| | 1 | | 2 | |
x1 = |
| (1.5 + |
| ) = 0.75 + 0.66 = 1.41 |
| | 2 | | 1.5 | |
oma!
10 lip 21:21
Trivial: Jeżeli potrzebujemy dokładniejszego przybliżenia przechodzimy przez proces jeszcze raz.
| | 1 | | 2 | |
x2 = |
| (1.41 + |
| ) = ... |
| | 2 | | 1.41 | |
10 lip 21:23
ICSP: Nadal nie łapię:( skąd wiedziałeś że po 1,5 jest prawidłowy wynik?
10 lip 21:25
Trivial:
Nie wiedziałem.

No to weźmy np. 2.
a=2, x
0=2;
| | 1 | | 2 | | 1 | |
x1 = |
| (2 + |
| ) = |
| *3 = 1.5 |
| | 2 | | 2 | | 2 | |
x
2 = ... = 1.41.
10 lip 21:26
ICSP: Dziwne:( Może kiedyś to zrozumiem

Co z tymi zadaniami?
10 lip 21:27
TOmek: przyznam się ,ze w trygonometrii skupiłem sie głownie na równaniach trygonometrycznych, więc
raczej nie dam rady zrobić tego zadania, a co do tego z planimetrii, poddaje sie.. cały dzien
straciłem na te zadanie i nadal nic nie drgnęło.
10 lip 21:29
Trivial:
Mogę spróbować to z trygonometrią. Na trapezy jakoś nie mam ochoty...

10 lip 21:29
ICSP: no dobrze. Zrobię to zadanie z trapezem a Trivial postara się zrobić zadanie z
trygonometrii. Vax i Godzio wymyślą ci kolejne zadania.
10 lip 21:31
TOmek: Godzio, mieszać działy będę juz niedługo, zakupiłem parę ksiazek z zadaniami tylko i wyłącznie
z matur rozszerzonych, lecz na razie męcze kiełbase

10 lip 21:32
TOmek: akurat zadań to ja mam pod dostatkiem, ale dziekuje ,ze się o mnie martwisz

10 lip 21:33
Godzio:
Trivial To jest metoda "siecznych" może ? Robiłem coś nią kiedyś, a nie jestem pewien czy
to to samo .
10 lip 21:44
ICSP:
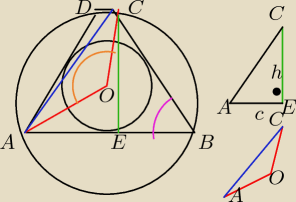
to wszystko jest styczne

Proszę nie bijcie za ten rysunek:(
Wyszło troszkę na to że okręgi są współśrodkowe:( no ale troszkę źle to narysowałem.
|AD| = c
|AB| + |DC| = 2c
OBW = 4c
P = c|EC|
| | √3 | |
różowy kąt ma 60o zatem oczywiste jest że h = |
| c |
| | 2 | |
Teraz rozpatrzmy trójkąt AOC układamy w nim twierdzenie cosinusów
kąt AOC = 120
o oraz |OA\ = |OC| = 1
|AC|
2 = 1 + 1 − 2cos120
o
|AC|
2 = 2 − (−1)
|AC|
2 = 3
|AC| =
√3
Teraz rozpatrujemy trójkąt ACE
c
2 + h
2 = |AC|
2
| | 2√21 | | √3 | | 6√7 | |
P = ( |
| )2 * |
| = |
| |
| | 7 | | 2 | | 7 | |
10 lip 21:46
Trivial:
Godzio to jest algorytm Newtona−kogoś.
10 lip 21:47
Trivial:
x = sin10
ocos20
ocos40
o
| | α−β | | α+β | |
sinα − sinβ = 2sin |
| cos |
| |
| | 2 | | 2 | |
α−β = 20
o
α+β = 40
o → β = 40
o − α
2α = 60
o
α = 30
o
β = 10
o
| | 1 | | 1 | | 1 | |
x = |
| (sin30o − sin10o)cos40o = |
| ( |
| − sin10o)cos40o = |
| | 2 | | 2 | | 2 | |
| | 1 | | 1 | |
= |
| cos40o − |
| sin10ocos40o. |
| | 4 | | 2 | |
α−β = 20
o
α+β = 80
o → β = 80
o − α
2α = 100
o
α = 50
o
β = 30
o
| | 1 | | 1 | | 1 | |
sin10ocos40o = |
| (sin50o − sin30o) = |
| sin50o − |
| |
| | 2 | | 2 | | 4 | |
| | 1 | | 1 | | 1 | | 1 | |
x = |
| cos40o − |
| ( |
| sin50o − |
| ) = |
| | 4 | | 2 | | 2 | | 4 | |
| | 1 | | 1 | | 1 | | 1 | | 1 | |
= |
| cos40o − |
| sin50o − |
| = |
| (cos40o − sin50o) − |
| . |
| | 4 | | 4 | | 8 | | 4 | | 8 | |
sin50
o = sin(90
o−40
o) = cos40
o.
Coś mi się zdaje, że jest jakaś prostsza droga.

10 lip 22:00
ICSP: | | cos10o | |
yyy przemnóż przez |
| |
| | cos10o | |
10 lip 22:02
TOmek: hoho, te zadanie z trygonometrią, przesada

10 lip 22:04
Trivial: | | sin80o | |
Wcześniej tak robiłem, ale się zawiesiłem jak otrzymałem |
| .  |
| | 8cos10o | |
10 lip 22:04
Trivial: Metody dookoła świata i tak są lepsze.


10 lip 22:05
ICSP: no nie gadaj. sin80o = cos10o. Na tym sie zawiesiłeś?
10 lip 22:05
Basia:
Trivial dlaczego się "zawiesiłeś" ?
cos10 = cos(90−80) = sin80
10 lip 22:07
Trivial:
Ostatnio takie zadania rozwiązywałem rok temu.

10 lip 22:07
TOmek: ICSP: a skąd wiesz ,ze AOC=120?
10 lip 22:08
Trivial: Tak wiem
Basiu, wpadłem na to w moim rozwiązaniu dookoła świata (pod koniec). Nie chciało
mi się już usuwać i od nowa robić więc wysłałem.

10 lip 22:08
10 lip 22:10
Trivial: Tak w ogóle to jest literówka w tym moim jakże genialnym rozwiązaniu.

Pod koniec zamiast −
powinien być +, ale wynik dobry.
10 lip 22:10
TOmek: Dziekuje ICSP

10 lip 22:12
ICSP: Nie ma za co
 Godzio
Godzio albo
Vax podali już zadanka?
10 lip 22:14
TOmek: ja już nie chce od Was zadań, mam niemiłe doświadczenie po dzisiejszym dniu


10 lip 22:21
ICSP: ej nawet z pazdro nie zaczęliśmy

10 lip 22:26
 Na płaszczyźnie z układem współrzędnych dane sa punkty A i B oraz proste k i l tworzące z
prostą o równaniu y=0 kąty o równych miarach(patrz rysunek).
a) wyznacz równania prostych k i l
b)Oblicz tangens kąta β
A=(4,4)
B=(−5,2)
Na płaszczyźnie z układem współrzędnych dane sa punkty A i B oraz proste k i l tworzące z
prostą o równaniu y=0 kąty o równych miarach(patrz rysunek).
a) wyznacz równania prostych k i l
b)Oblicz tangens kąta β
A=(4,4)
B=(−5,2)
 ? A nie robić "kilka dni" samemu, aż się
uda
? A nie robić "kilka dni" samemu, aż się
uda  ? Lub czytać o tym co można wykorzystać w danym zadaniu.
a) https://matematykaszkolna.pl/strona/1212.html
b) https://matematykaszkolna.pl/strona/1228.html
? Lub czytać o tym co można wykorzystać w danym zadaniu.
a) https://matematykaszkolna.pl/strona/1212.html
b) https://matematykaszkolna.pl/strona/1228.html

 No to tak:
Masz proste "k i l". Prosta k załóżmy, że jest rosnąca, czyli jej a > 0 (a) i przechodzi przez
punkt A(4,4). Prostą "l" załóżmy, że jest malejąca czyli a<0 (−a) i przechodzi przez punkt
B(−5,2).
Kluczowym w tym zadaniu jest wykorzystanie wiedzy z: https://matematykaszkolna.pl/strona/1212.html.
Wpierw jednak oznaczmy sobie jakoś
równania tych prostych: Prostą "k" jako np.: y = ax + b, natomiast prostą "l" jako: y = a'x +
b'. Korzystając z tego linka wyżej mamy: a = tgα (to wiadome). Natomiast dla prostej "l − tej
malejącej" mamy tg(180o − α) [naprawdę to na rysunku te kąty to:
β + α]. Dobra to teraz czas na wzory redukcyjne tg(180o − α) = −tgα = −a. Czyli a' = −a.
Kolejna obserwacja kluczowa to to, że mają wspólne miejsce zerowe. Czyli mamy:
No to tak:
Masz proste "k i l". Prosta k załóżmy, że jest rosnąca, czyli jej a > 0 (a) i przechodzi przez
punkt A(4,4). Prostą "l" załóżmy, że jest malejąca czyli a<0 (−a) i przechodzi przez punkt
B(−5,2).
Kluczowym w tym zadaniu jest wykorzystanie wiedzy z: https://matematykaszkolna.pl/strona/1212.html.
Wpierw jednak oznaczmy sobie jakoś
równania tych prostych: Prostą "k" jako np.: y = ax + b, natomiast prostą "l" jako: y = a'x +
b'. Korzystając z tego linka wyżej mamy: a = tgα (to wiadome). Natomiast dla prostej "l − tej
malejącej" mamy tg(180o − α) [naprawdę to na rysunku te kąty to:
β + α]. Dobra to teraz czas na wzory redukcyjne tg(180o − α) = −tgα = −a. Czyli a' = −a.
Kolejna obserwacja kluczowa to to, że mają wspólne miejsce zerowe. Czyli mamy:


 ?
Trudniejsze zadania?
Jakim ty systemem jedziesz
?
Trudniejsze zadania?
Jakim ty systemem jedziesz  ?
?

 I nawet proste są
podpisane, więc będziesz musiał zmienić trochę oznaczeń
I nawet proste są
podpisane, więc będziesz musiał zmienić trochę oznaczeń 
 czyli druga
czyli druga 

 Co do ksiązki kiełbasy, nie zgadzam sie z Tobą. Jest to jedna z nielicznych
ksiązek, która jest sprawdzona przez wielkie grono osób, które pozytywnie sie o niej
wypowiadali. Moj kumpel przygotowywał sie tyko na kiełbasie i napisał swietnie maturke
Co do ksiązki kiełbasy, nie zgadzam sie z Tobą. Jest to jedna z nielicznych
ksiązek, która jest sprawdzona przez wielkie grono osób, które pozytywnie sie o niej
wypowiadali. Moj kumpel przygotowywał sie tyko na kiełbasie i napisał swietnie maturke 

 Poza tym na razie nie robię w ogóle zadań, tylko przeglądam te forum
Poza tym na razie nie robię w ogóle zadań, tylko przeglądam te forum  Coś myślę, że tak do końca lipca będę umiał dość dobrze kombinatorykę, a do września
stereometrie. Za prawdopodobieństwo wezmę się we wrześniu i idę na maturkę
Coś myślę, że tak do końca lipca będę umiał dość dobrze kombinatorykę, a do września
stereometrie. Za prawdopodobieństwo wezmę się we wrześniu i idę na maturkę 



 Sam musisz wpaść na rozwiązanie. Wtedy gwarantuje ci że zapamiętasz sposób
robienia takich zadań do końca życia.
Sam musisz wpaść na rozwiązanie. Wtedy gwarantuje ci że zapamiętasz sposób
robienia takich zadań do końca życia.


 Odp.
Odp.  dobra to pierw zajme sie zadanie rumpka:
troche mi obrazek nie wyszedł
dobra to pierw zajme sie zadanie rumpka:
troche mi obrazek nie wyszedł
 Poza tym kiedyś już dodawałeś to zadanie
Poza tym kiedyś już dodawałeś to zadanie  https://matematykaszkolna.pl/forum/64074.html
dlatego je umieściłem
https://matematykaszkolna.pl/forum/64074.html
dlatego je umieściłem 
 ale na oko dobrze jest?
ale na oko dobrze jest?
 Kiedyś je robiłeś powinieneś pamiętać. Ja zrobiłbym sposobem całkiem innym:
No i teraz patrzę na h i x, chcę te oznaczenia otrzymać więc:
Kiedyś je robiłeś powinieneś pamiętać. Ja zrobiłbym sposobem całkiem innym:
No i teraz patrzę na h i x, chcę te oznaczenia otrzymać więc:

 Jednakże, Kiełbasa jak to bywa podaje inne odpowiedzi
Jednakże, Kiełbasa jak to bywa podaje inne odpowiedzi  np.:
Podstawa:
np.:
Podstawa:
 Także myślę, że błędu nie popełniłem
Także myślę, że błędu nie popełniłem  a kiełbasa to kiełbasa
a kiełbasa to kiełbasa  zawsze jakieś trudniejsze
sposoby znajdzie
zawsze jakieś trudniejsze
sposoby znajdzie 

 Jak dla mnie to zrobię je jutro, bo zaraz szykuję się do
spania, bo o 5 trzeba wstać
Jak dla mnie to zrobię je jutro, bo zaraz szykuję się do
spania, bo o 5 trzeba wstać .
Zadanie nie wydaje się trudne, skorzystałbym przede wszystkim z :
https://matematykaszkolna.pl/strona/874.html
Pierwsza zależność, no i oczywiście jakieś tam zależności sinusów cosinusów itp.
.
Zadanie nie wydaje się trudne, skorzystałbym przede wszystkim z :
https://matematykaszkolna.pl/strona/874.html
Pierwsza zależność, no i oczywiście jakieś tam zależności sinusów cosinusów itp.  Ale to
trzeba zadanie zrobić
Ale to
trzeba zadanie zrobić 
 Przecież to jego temat
Przecież to jego temat Niech ma troszkę trudniejsze zadania.
Niech ma troszkę trudniejsze zadania.



 wiem ,zajebisty obrazek
wiem ,zajebisty obrazek  180−60=120
12+12=c2
c=√2
180−60=120
12+12=c2
c=√2

 i odrazu mam pytanie, bo znam taką zależność ,ze jak okrąg jest wpisany w czworokąt to trójkąt
(ten na obrazku) jest prostokątny, lecz jak to udowodnić
i odrazu mam pytanie, bo znam taką zależność ,ze jak okrąg jest wpisany w czworokąt to trójkąt
(ten na obrazku) jest prostokątny, lecz jak to udowodnić


 .
.
 według ciebie zależności w takim trapezie wyglądają następująco. Teraz pytanie do ciebie: Ile
będą miały kąty przy podstawie oraz przy wierzchołku skoro czerwone odcinki są identyczne?
według ciebie zależności w takim trapezie wyglądają następująco. Teraz pytanie do ciebie: Ile
będą miały kąty przy podstawie oraz przy wierzchołku skoro czerwone odcinki są identyczne?
 180+α+β=360
180+α+β=360
 Ty masz chyba fajne zadanko do rozwiązania
Ty masz chyba fajne zadanko do rozwiązania

 180−60=120o
wiemy ,że
180−60=120o
wiemy ,że


 ale to dzisiaj o 6 robiłem
ale to dzisiaj o 6 robiłem  także mogłem coś pokręcić, a wyniku nie zapisałem
także mogłem coś pokręcić, a wyniku nie zapisałem 


 a tu trzy próby i
zero pomysłu z "Twojej strony" ...
a tu trzy próby i
zero pomysłu z "Twojej strony" ...
 że banalne to ty napisałeś... Ja odpowiedziałem − skoro takie łatwe to czemu nie
rozwiązałeś?
że banalne to ty napisałeś... Ja odpowiedziałem − skoro takie łatwe to czemu nie
rozwiązałeś?
 ICSP Wracając do tego co napisał TOmek z kątem prostym w trapezie równoramiennym, to
ma on racje, zauważ, że w trapezie równoramiennym kąty przy tej samej podstawie są równej
długości, dodatkowo środek okręgu wpisanego wyznaczony jest oczywiście przez dwusieczne kątów
czworokąta, teraz korzystając z tego, że suma miar kątów w czworokącie wynosi 360* mamy:
4α+4β = 360 /:4 ⇔ α+β = 90* czyli istotnie kąt DOA = kąt BOC = 180−(α+β) = 90*
ICSP Wracając do tego co napisał TOmek z kątem prostym w trapezie równoramiennym, to
ma on racje, zauważ, że w trapezie równoramiennym kąty przy tej samej podstawie są równej
długości, dodatkowo środek okręgu wpisanego wyznaczony jest oczywiście przez dwusieczne kątów
czworokąta, teraz korzystając z tego, że suma miar kątów w czworokącie wynosi 360* mamy:
4α+4β = 360 /:4 ⇔ α+β = 90* czyli istotnie kąt DOA = kąt BOC = 180−(α+β) = 90*  Pozdrawiam.
Pozdrawiam.

 TOmek a powiem ci tyle, że wcale nie jestem dobry z matmy, mam jeszcze większe problemy
niż ty
TOmek a powiem ci tyle, że wcale nie jestem dobry z matmy, mam jeszcze większe problemy
niż ty 

 Pozdrawiam.
Pozdrawiam.



 o to chodzi? prawda?
o to chodzi? prawda? 




 My chcemy ci pomóc sie rozwinąć. Oczywiście jakiś PRO może
podać odpowiedzi bo jestem pewien że ktoś już to rozwiazał
My chcemy ci pomóc sie rozwinąć. Oczywiście jakiś PRO może
podać odpowiedzi bo jestem pewien że ktoś już to rozwiazał
 Teraz wystarczy że znajdziesz sposób rozwiązania
Teraz wystarczy że znajdziesz sposób rozwiązania

 2x=a−b
a+b=2c
2x=a−b
a+b=2c

 Ja to wyliczyłem zauważając, że promień okręgu opisanego na trójkącie BDC jest równy promieniu
okręgu opisanego na trapezie ABCD
Ja to wyliczyłem zauważając, że promień okręgu opisanego na trójkącie BDC jest równy promieniu
okręgu opisanego na trapezie ABCD 


 Jedyny temat na forum w którym coś się dzieje. Trivialku nie
znasz przypadkiem jakiejś metody itteracyjnej?
Jedyny temat na forum w którym coś się dzieje. Trivialku nie
znasz przypadkiem jakiejś metody itteracyjnej?




 Znam tylko iteracyjną metodę pierwiastkowania.
Znam tylko iteracyjną metodę pierwiastkowania.

 Ja osobiście
do tego typu zadań stosuję metodę bisekcji, przystępnie opisali jej działanie na wiki:
http://pl.wikipedia.org/wiki/Metoda_r%C3%B3wnego_podzia%C5%82u
Jeżeli szukamy przybliżenia wartości √3, to wystarczy zastosować daną metodę dla wielomianu
W(x) = x2−3, zaczynając np od przedziału [1;2]
Ja osobiście
do tego typu zadań stosuję metodę bisekcji, przystępnie opisali jej działanie na wiki:
http://pl.wikipedia.org/wiki/Metoda_r%C3%B3wnego_podzia%C5%82u
Jeżeli szukamy przybliżenia wartości √3, to wystarczy zastosować daną metodę dla wielomianu
W(x) = x2−3, zaczynając np od przedziału [1;2]  Pozdrawiam.
Pozdrawiam.
 No to weźmy np. 2.
a=2, x0=2;
No to weźmy np. 2.
a=2, x0=2;
 Co z tymi zadaniami?
Co z tymi zadaniami?



 to wszystko jest styczne
to wszystko jest styczne Proszę nie bijcie za ten rysunek:(
Wyszło troszkę na to że okręgi są współśrodkowe:( no ale troszkę źle to narysowałem.
|AD| = c
|AB| + |DC| = 2c
OBW = 4c
P = c|EC|
Proszę nie bijcie za ten rysunek:(
Wyszło troszkę na to że okręgi są współśrodkowe:( no ale troszkę źle to narysowałem.
|AD| = c
|AB| + |DC| = 2c
OBW = 4c
P = c|EC|








 Pod koniec zamiast −
powinien być +, ale wynik dobry.
Pod koniec zamiast −
powinien być +, ale wynik dobry.

 Godzio albo Vax podali już zadanka?
Godzio albo Vax podali już zadanka?


