Kombinatoryka helmut: zad 1 Rzucamy 2 razy kostkę do gry oblicz prawdopodobieństwo wylosowania liczby parzystej . zad 2 Z talii 52 kart na ile sposobów można wylosować 3 króle i 2 kiery

helmut: nikt nie jest w stanie mi pomóc

:P: już chwila.

8: 1. |Ω|=6x6=36 A−wylosowano liczbę parzystą za pierwszym razem może być cyfra od 1,2,...,6 a na drugim miejscu tylko liczby parzyste czyli 2,4,6 |A|= 6x3=18 P(A) =18/36 =0,5

helmut: mogę się dowiedzieć dlaczego |A|= 6*3 ?

:P: 1017 rzucasz 2 razy, i obliczyć prawdopodobieństwo że wylosowano liczbę parzystą. czyli ja to rozumiem tak, ze przynajmniej raz w tych dwóch rzutach wypadła liczba parzysta. Mamy więc możliwości, że wypadają albo 2 razy parzyste, albo za pierwszym razem parzysta, albo za drugim razem parzysta.Zauważ, że prawdopodobieństwo wypadnięcia w pojedynczym rzucie liczby parzystej wynosi ¹₂. −−−−> no bo mamy 3 parzyste i 3 nieparzyste pół na pół. i teraz 3 przypadli. I tak samo prawdopodobieństwo ze wypadnie nieparzysta też jest ¹₂ −−−−−−>wypadła dwa razy liczba parzysta P₁ = ¹₂ * ¹₂ = ¹₄ <−−− za pierwszym razem parzysta(¹₂) oraz za drugim razem parzysta (¹₂) −−−−−−−−−>za pierwszym razem parzysta, ale za drugim razem nie (ale warunek spełniony bo jedna parzysta wypadła) P₁ = ¹₂ * ¹₂ = ¹₄ <−−−−−−<−−− za pierwszym razem parzysta(¹₂) oraz za drugim razem nieparzysta (¹₂) −−−−−−−>za pierwszym razem nieparzysta, ale za drugim razem parzysta P₃ = ¹₂ * ¹₂ = ¹₄ <−−−−−−<−−− za pierwszym razem nieparzysta(¹₂) oraz za drugim razem parzysta (¹₂) I teraz prawdopodobieństwo tego że wylosowano przynajmniej raz liczbę parzystą to suma. P = P₁ + P₂ + P₃ = ¹₄ + ¹₄ + ¹₄ = ³₄ <−−−−−−Odp.

7: bo tak jak rzucasz 2 razy to otrzymujesz cyfry od 1 do 6 i żeby ta liczba dwu cyfrowa była parzysta to na drugim miejscu moze mieć tylko cyfry parzyste czyli 2,4, 6 i ich jest 3 a pierwsza cyfra liczby nie decyduje czy ona jest parzysta czy nie parzysta wiec może być cyfra od 1 do 6 a Ω ={ (a,b) ; a,b ∊ {1,2,3,4,5,6} }

helmut: to może teraz zadanie 2 ? bo 1 wytłumaczył mi ładnie 8:

:P: własnie o co dokładnie chodzi w zadaniach

:P: króli jest 4 a kierów 13

4 3		13 2
	*		<−−−−ponieważ z 4 losujemy 3 i z 13 losujemy 2

4 3		13 2
	*		= 4 * 11! * 12 * 1311! * 2! = 6*13 = 78

:P: aajjjj osrka jeszcze źle

Ania: Oblicz odległość między prostymi równoległymi o równaniach y=−2x+2 i y=−2x−4

8: masz wyniki do tych zadań

helmut: czyli jak bym losował z 52 kart 2 króle to będzie

4 2		4!
	=		= 6
		(4−2)!*2!

dobrze ?

:P: dlatego ze może być król kier, czyli pierwszy przypadek. zakładamy ze te 3 króle są inne niż kier(jest jeden taki przypadek)i wtedy losujemy to tego 2 z 13 kiery

	13 2
1 *		= 78

drugi przypadek. zakładamy ze wśród tych króli jest kier (jest takie 3 możiwości) i wtedy potrzeba nam już tylko jednego kiera z 12

	1 12
3 *		= 3*12 = 36

78+36 = 114 masz może odpowiedzi

Ania: Oblicz odległość między prostymi równoległymi o równaniach y=−2x+2 i y=−2x−4

helmut: niestety nie mam

:P:

	4 2
jest		bo losujesz 2 króle z 4 króli

8: omega moc to w szkole tak pisze się = Ω coś takiego z dwoma kreskami u góry i A moc też z dwoma kreskami poziomymi u góry

:P: rozumiesz helmut?

helmut: no czyli dobrze zrobiłem wyszło 6

Ania: Oblicz odległość między prostymi równoległymi o równaniach y=−2x+2 i y=−2x−4

:P: ale wyżej masz ogólnie wychodzi mi 114.widzisz?

helmut: no tak ale ja wyliczyłem tylko 2 króle bez kierów to jest inny przykład zadania tak żeby się sprawdzić

:P: dla ANIA. przekształcasz funkcje do wzoru (poprostu przenosisz na jedną strone) Ax + By + C = 0 i mamy wtedy. −2x −y + 2 = 0 oraz druga −2x −y −4 = 0 teraz widzisz, że A to −2 dla obu, B to −1 dla obu, oraz c to 2 i −4 wzór na odległość: d = |C₁ − C₂| przez √A² + B² d = ^|2+4|_√5 = ⁶_√5 = ^6√5₅

Ania: Czy ktoś mi pomoże

Ania: Dziękuję

:P: ok helmut zgadza się. na przykład jeśli chcesz wiedzieć ile jest możliwości wyboru 3 osób z klasy która liczy 30 uczniów.

	30 3
To liczysz		−−−−>1014

:P: ania sprawdź sobie jeszcze obliczenia, ja się posłużyłem tą stroną, przeczytaj http://www.matematyka.pl/30225.htm

Ania: Oblicz odległość między środkami okręgów o równaniach: (x−4)²+(y+2)²=16 i (x−1)²+(y+1)²=1.

Ania: Pomocy

8: chwilka zaraz bedzie

8: srodkiem okręgu (x−4)² + (y+2)²=16 jest S(4, −2) a srodkiem drugiego (x−1)²+ (y+1)²=1 jest O(1,−1) teraz policzymy odległość miedzy dwom punktami |SO|=√(1−4)² + (−1−(−2))²=√ 3²+1²= √10

Ania: Napisz równanie okręgu opisanego na prostokącie KLMN, w którym dane są przeciwległe wierzchołkami K(0;−3) i M(6;5)

Ania: Proszę o pomoc

Ania: Pomożecie

Ania: Napisz równanie okręgu opisanego na prostokącie KLMN, w którym dane są przeciwległe wierzchołkami K(0;−3) i M(6;5).

Ania: Proszę o pomoc

:P: już robie ^^

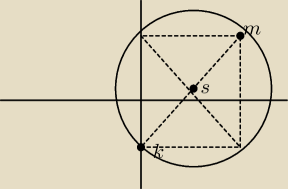
podpis.: K(0,−3) oraz M(6,5) −−−> 1468 <−−−− równanie okręgu. (x−a)² + (y−b)² = r² a i b to współrzędne środka, a r to promień zauważmy na rysunku, że s to punkt przecięcia sie przekątnych prostokąta, czyli środek prostej |MK|, a r to odległość |KS| albo |SM|. Umiemy policzyć środek odcinka −−−−> 1750 oraz odległość punktu od punktu −−−> 1248. No to liczymy. S = (⁰⁺⁶₂; ⁻³⁺⁵₂) = (3; 1) <−−−−− no i już mamy a=3 i b=1 teraz odległość (czyli promień) r = √(0−3)² + (−3−1)² = √9 + 16 = √25 = 5, czyli r² = 25 i podstawiamy do wzoru. −−−−> (x−a)² + (y−b)² = r² (x−3)² + (y−1)² = 25 <−−−−−− nasza odpowiedź.