Praca kontrolna Andzia: Witam.! Potrzebuję pomocy: 1. Jedna z przyprostokątnych trójkąta jest 3 razy krótsza od drugiej przyprostokątnej. Długość przeciwprostokątnej wynosi 20. Oblicz długość przyprostokątnej. 2. Dana jest prosta l:y=2x+7. Napisz równanie prostej k, przechodzącej przez punkt K=(−4, −10) i równoległej do prostej l. 3. Wyznacz środek i promień okręgu o równaniu x²+y²−10x+6y+18=0. 4.Dany jest równoległobok ABCD , gdzie A=(1,−1), B=(5,7), D=(−2,3). Oblicz pole tego równoległoboku. 5. Punkty A=(−2,4), C=(4,10) są przeciwległymi wierzchołkami rombu ABCD. Wyznacz równanie prostej zawierającej przekątną BD tego rombu. Proszę Was o pomoc nad tymi zadaniami. Z góry dziękuję

sushi_ gg6397228: Pitagoras x²+(3x)²=20² x²+9x²=400 10x²=400 x²=.... ==> x=.... 3x=.... 2. y=ax+b wiec prosta rownolegla y₁= a x + b₁ ( ma ten sam wspolczynnik kierunkowy) czyli a=2 mamy punkt K(−4,−10) −10= 2* (−4) +b₁ −10=−8 +b₁ b₁=−2 wzor rownoleglej: y=2x−2 3. wzor okregu x²−2ax+ y² −2by +a²+b²−r²=0 ( w postaci rozwinietej) (x−a)²+(y−b)²=r² ( w postaci zwinietej) srodek okregu S=(a,b) r− promien x²+y²−10x +6y+18=0 x² −2ax+ y² −2by +a²+b²−r²=0 porownujemy odpowiednie liczby ( patrz kolory czerwony i niebieski) −10=−2a 6= −2b a=5 b=−3 i podstawimy pod kolor zielony ("a" i "b") 18=a²+b²−r² 18= 25+9 −r² r²=16 (r=4) S=(5,−2) r=4

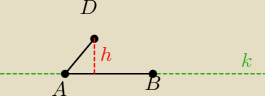sushi_ gg6397228: 4. 1 krok dlugosc odcinka AB |AB|=√(x_B−x_A)² + (y_B−y_A)² podstawiamy wspolrzedne punktow |AB|=√(5−1)²+(7−(−1))² |AB|=√16+64 |AB|=√80 |AB|=√16*5 |AB|=√16*√5 |AB|=4√5 2krok prosta przechodzaca przez 2 punkty https://matematykaszkolna.pl/strona/1223.html osobisicie wole rozwiazywac uklad rownan dla prostej y=ax+b A(1,−1), B(5,7) −1=a*1 +b ( obustronnie mnoze przez −1) 7=a*5 +b 1=−a−b + 7=5a+b −−−−−−−−−−−−−−−−−−−− 8= 4a a=2 i podstawiam do wyjsciowego np −1=a+b −1=2+b b=−3 zatem prosta ma postac : y= 2x−3 ( postac kierunkowa) w dalszej czesci zadania bedzie potrzebna postac ogolna prostej Ax+By+C=0, wiec 2x−1y−3=0 (A=2, B=−1, C=−3) 3 krok odleglosc punktu od prostej ( aby policzyc wysokosc) punkt D(−2,3) https://matematykaszkolna.pl/strona/1249.html

	|2*(−2) − 1*(3) −3|
h=
	√22+12

	|−10|
h=
	√5

	10
h=
	√5

4 krok pole rownolegloboku P=|AB|*h

	10
P=4√5 *
	√5

P=40[j²]

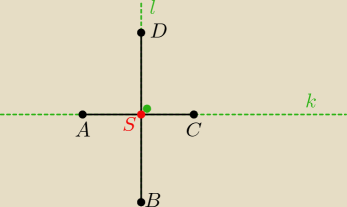sushi_ gg6397228: 5. romb przekatne przecinaja sie w polowie pod katem prostym 1. krok srodek odcinka AC https://matematykaszkolna.pl/strona/1750.html

	−2+4		4+10
S=(		;		)
	2		2

S=(1;7) 2 krok prosta przechodzaca przez punkty A i C y=ax+b 4= a*(−2) +b (obustronnie pomnozone przez "−1") 10= a*4 +b −4=2a −b + 10= 4a+b −−−−−−−−−−−−−−−−−−−−−−−− 6= 6a a=1 i podstawiamy np 10=4a+b 10=4*1+b b=6 wzor prostej y=x+6 2 krok prosta prostopadla przechodzaca przez punkt S (1,7) https://matematykaszkolna.pl/strona/42.html k: y=1x+6

	−1
l: y=		x +b1
	1

l: 7=−1*(1)+b₁ 8=b₁ l: y=−x+8 prosta przechodzaca przez punkty B i D (druga przekatna)

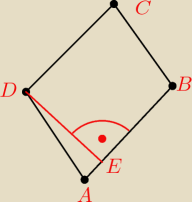Januszek75: 1. obliczyć prostą przechodzącą przez pkt. A i pkt.B 2. obliczyc długość AB 3. wyznaczyc odleglosc pkt.D od prostej AB 4. obliczyc pole P=DE*AB