równanie symetralnej odcinka AB betsy: Wyznacz równanie symetralnej odcinka AB, jeżeli A=(−4,−6), B=(2,−4) jak się takie rzeczy liczy?Nigdy nie robiliśmy w szkole takch zadań może ktoś wytłumaczyć krok po kroku?

Godzio: pomoge ... z wytłumaczeniem

Godzio: Symetralna − prosta przechodząca przez środek danego odcinka i padająca na niego pod kątem prostym. Po pierwsze trzeba wyliczyć prostą y_AB Sp. 1 przez układ równań A(−4,−6) B(2,−4) podsatwiajac pod wzór y = ax + b −6 = −4a + b −4 = 2a + b − −−−−−−−−−−−−−−−−− −2 = − 6a

	1
a =		( b nam nie potrzebne bo chodzi o prostą prostopadła ale wylicze)
	3

	2
b = −4
	3

Sp. 2 podstawić punkty pod wzór: https://matematykaszkolna.pl/strona/1223.html Teraz liczymy środek odcinka AB :

	−4+2		−6 − 4
S = [		,		] = [ −1 , −5 ]
	2		2

S(−1,−5) Współczynnik kierunkowy prostej prostopadłaj liczymy ze wzoru: a * a₁ = − 1 a₁ = −3 Symetralna ma współczynnik kier. − 3 i przechodzi przez punkt S, więc podstawiamy dane i wyliczamy "b" . y = ax + b −4 = −3 * (−1) + b −4 = 3 + b b = −7 Równanie symetralnej: y = −3x − 7

betsy: dziękuję bardzo mocno za pomoc

betsy: tylko tam będzie −5=−3*(−1)+b

Godzio: rzeczywiście

Gustlik: Godzio − do wyznaczenia prostej przechodzącej przez dwa punkty nie potrzeba układu równań. Ja to robię tak: współczynnik kierunkowy prostej wyliczam ze wzoru:

	yB−yA
a =
	xB−xA

	−4−(−6)		−4+6		2		1
a =		=		=		=
	2−(−4)		2+4		6		3

Podstawiam obliczone a do równania prostej:

	1
y =		x + b
	3

Podstawiam współrzędne któregoś z punktów A lub B, np. B=(2, −4) − zazwyczaj wybieram ten punkt, który ma "ładniejsze" i łatwiejsze do obliczania współrzędne:

	1
−4 =		*2 + b
	3

	2
−4 =		+ b
	3

	2
−4 −		= b
	3

	2
b = −4
	3

Prosta AB ma równanie:

	1		2
y =		x − 4
	3		3

Ciąg dalszy z obliczaniem symetralnej − tak samo, jak u Ciebie.

Bogdan: Można również podstawić współczynnik a do równania: y = a(x − x₀) + y₀, gdzie punkt (x₀, y₀) to punkt, przez który przechodzi prosta. W tym zadaniu wystarczy wyznaczyć współczynnik kierunkowy a_AB prostej zawierającej

	1
punkty A i B: aAB =		.
	3

Symetralna do AB przechodzi przez punkt S(−1,−5), współczynnik kierunkowy symetralnej a_S = −3 y = −3(x + 1) − 5 ⇒ y = −3x − 8

Majkrus: Ludzie uratowaliscie mi tym postem zycie! jutro mam wazny spr z matmy i tez nie ogarnialem jak to sie robi ale dzieki wam juz to ogarniam wielkie dzieki ^^

Aga: Można rozwiązać jeszcze innym sposobem.Punkt P(x,y) należy do symetralnej odcinka AB, jeśli IAPI=IBPI √(x+4)²+(y+6)²=√(x−2)²+(y+6)² x²+8x+16+y²+12y+36=x²−4x+4+y²+8y+16 12x+4y+32=0 y=−3x−8.

zbyszek: symetralne odcinka A(−5,2) B(3,−1)napisz rownanie

natalia: ale symetralna ma −1,−5 wiec czemu tam zmiast −5 jest 4 ?!?!?

5-latek: Natalio . Symetralna to nie jest −1,−5 tylko to sa wspolrzedne srodka odcinka |AB|. Natomiast symetralna to jest prosta ktora jest prostopadla do tego odcinka i przechodzi przez jego srodek . https://matematykaszkolna.pl/strona/3385.html zobacz tutaj wiec musi by postaci y=ax+b Wiec napisz czego nie rozumiesz .

natalia: kurcze.... wogóle nie rozumie jak mam tą symetralną wyliczyć z odcinka AB lub odcinka AC obojętnie jakie miałoby mieć dane. Jakiś prosty sposób jak to wyliczyć, skąd to wychodzi? Błagam pomocy ;<

bezendu: https://matematykaszkolna.pl/strona/3385.html

5-latek: https://matematykaszkolna.pl/strona/1750.html masz tu wzor na srodek odcinka . Narysuj sobie teraz uklad wspolrzednych i zaznacz ponkt A(−2,−5)i punkt B(3,7) ( te punkty podalem z glowy zeby Ci pokazac jak to zrobic) Polacz te dwa punkty i dostaniemy odcinek |AB| . Przyjmij ze punkt A jest poczatkiem odcinka |AB| a punkt B kocem tego odcinka . Jesli punkt A(−2,−5) jest poczatkiem odcinka |AB| to jego wspolrzdne sa rowne x₁=−2 i y₁= Teraz jesli pubkt B(3,7) jest koncem tego odcinka to jego wspolrzedne sa rowne x₂=3 i y₂=7 Przepisz sobie ten wzor z linka co CI podalem i patrz na niego Mamy tam podane jak wyliczc srodekS odcinka|AB| −czyli jesgo wspolrzedne x_s i y_s

	x2−x1		3−(−2)		3+2
Mamy tak xs=		=		=		=2,5
	2		2		2

	y2−y1		7−(−5)		7+5
ys=		=		=		=6 i takie wspolrzedne ma nasz
	2		2		2

punkt S czyli S(2,5,6) No to teraz wyznacz wspolrzedne srodka odcinka majac dane A(1,6) i B(4,−5) zobacze czy to rozumiesz. Najpierw to a potem do wyznaczenia rownania symetralnej .

5-latek:

	x1+x2		−2+3		y1+y2		−5+7
Przepraszam mialo byc xs=		=		=0,5 i ys=		=		=1.
	2		2		2		2

Wiec srodek ma wspolrzedne S(0,5,1) POmylilo mi sie zwyznaczeniem wspolczynnika prostej .

natalia: No oblicznie środkowej małe piwo nie wiem tylko co dalej z tą całą symetralną znalazłam fajny wzór powiedz mi czy on sie zawsze sprawdzi : y=a*(x−x_y)+y_s . Co do zadania które mi

	3
podałeś S(1,5 ; −5,5) dlatego, że wyszedł mi ułamek z x =		no i z tego wychodzi 1,5
	2

	−11
oraz y=		czyli z tego wychodzi 5,5
	2

natalia: cholera ja to odjełam −,− Przepraszam..

	5		1
S(		,		) czyli S (2,5 ; 0,5)
	2		2

5-latek: Natalio nie przepraszaj bo ja sie tez pomylilem Tak to bedzie ten wzor . Tylko ze musimy znac jaki bedzie wsoilczynnik a tej prostej prostopadlej Wezmy te dwa punkty A(1,6) i B (4,−5) Srodek S juz mamy wyliczony . Wiec tak . Policzmymy jaki jest wspolczynnik kierunkowy prostej AB . czyli wzor

	y2−y1
a=		wiec policz ile wynosi
	x2−x1

5-latek: i napisz tutaj bo bedziemy dalej liczyc

natalia:

	11		3
a=−		czyli teraz trzeba to odwrócic i dac przeciwstawny znak? wiec będzie a=
	3		11

5-latek: Tak . Bo warunek prostopadlosci prostych jest a*a₁=−1 . Wiec teraz do tego wzoru (jest to wzor na prosta przechodzaca przez 1 punkt ) podstaw za a=3/11 i wsolrzede punktu S i napisz rownanie symetralnej tutaj to CI jeszce cos ppokaze .

bezendu: Witaj 5−latku mogę napisać swoje rozwiązanie ?

5-latek: Alez oczywiscie

natalia:

	3
y=		* (x−6)+0,5
	11

	3		18
y=		x −		+0,5
	11		11

	3		235
y=		x+
	11		110

bez sensu ten wynik

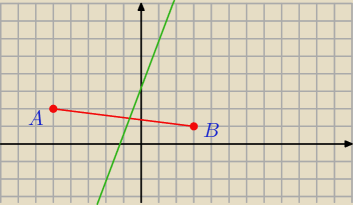
bezendu: Sposób który pokazała Mila A=(−5,2) B=(3,−1) √(x+5)²+(y−2)²=√(x−3)²+(x+1)² (x+5)²+(y−2)²=(x−3)²+(y+1)² x²+10x+25+y²−4y+4=x²−6x+9+y²+2y+1 −6y+16x+19=0 −6y=−16x−19

	8		19
−y=−		x−		/(−1)
	3		6

	8		19
y=		x+
	3		6

5-latek:

	3
y=		(x−x0)+y0
	11

	3
y=		(x−2,5)+05
	11

	3		3		5		1
y=		x−		*		+
	11		11		2		2

	3		15		1
y=		x−		−
	11		22		2

	3		15		11
y=		x−		−
	11		22		22

	3		4
y=		x−
	11		22

bezendu: 5−latek jakie rozważacie punkty ? A=? B=?

5-latek: DObrze bezendu

natalia: aha, czyli mialam calkiem podstawic w tym wzorze wspolrzedne symetralnej? Ok to rozumie blad tyle ze we wzorze jest x_y jakbym miała wziąść dane z pkt A np.. Czyli zawsze mam drac tylko współrzędne środkowej danego odcinka?

5-latek: punktya(1,6) i B(4,−5)

bezendu: Ja napisałem rozwiązanie do punktów A=(−5,2) B=(3,−1) post godzina 08:19 14 listopad

bezendu: punkty A=(1,6) B=(4,−5) znowu sposób Mili √(x−1)²+(y−6)²=√(x−4)²+(x+5)² (x−1)²+(y−6)²=(x−4)²+(y+5)² x²−2x+1+y²−12y+36=x²−8x+16+y²+10y+25 −22y+6x−4=0 −22y=−6x+4

	3		2
−y=−		x+		/(−1)
	11		11

	3		2
y=		x−
	11		11

bezendu: A tu kilka sposobów na to zadanie https://matematykaszkolna.pl/forum/207007.html

5-latek: Natalio jesli wyznaczasz rownanie symetralnej to bierzesz srodek odcinka bo ona przechodzi przez srodek odcika i jest do niego prostopadla . Teraz jeszce popatrz Jesli masz dwa punkty (niech beda te nasze czyli A(1:6) i B(4;−5) jesli mialas wektory to wspolczynnik kierunkowy prostej przechodzacej przez te dwa punkty mozesz wyznaczyc tak AB→[x₂−x₁; y₂−y₁] to AB→[4−1; −5−6] to AB→[3,−11] [W_x;W−y] Teraz

	Wy		−11
a=		to a=		. bo tgα jest to kat nachylenia prostej do osi OX a z kola
	wx		3

	y
trygonometrycznego wynika ze tgα=		i teraz wyznaczny rownanie prostej przechodzacej
	x

przez te dwa punkty

	−11		−11
rownanie ma postac y=ax+b a my wiemy z enasze a=		to bedzie y+		x+b
	3		3

Bierzemy obojetnie ktory punkt _wezmy A(1;6) Wiemy ze jesli punkt nalezy do prostej to spelnia

	−11
jej rownanie wiec 6=		*1+b wiec wyznacz z tego b i napisz rownanie prostej
	3

przechodzaxej przez te dwa punkty czyli y=U−11}{3}x+ wyliczone b −proste ? pewnie ze tak

natalia: Aaaaaaaaa! haha Dobra rozumie już ! matko.. życie mi ratujesz i przepraszam za kłopot ale lewa jestem z maty xD

5-latek: Bezendu OK .

bezendu:

5-latek: To byla czysta przyjemnosc . Tylko mam prosbe . Poucz sie dodawania i odejmnowania ulamkow Przeciez wiesz ze jesli masz ulamki o rozmych mianownikack to musisz je soprowadziec do wspolnego manownika ..Jeszcze sie troche przyloz i bedzie gitara POwodzenia >

natalia: tak wiem, ja juz to pisalam pod totalnymi nerwami wiec mi sie juz mieszalo xd mam jeszcze sporo rzeczy do ogarniecia ale najwazniejsze ze chociaz ta symetralna zostala ogarnieta

5-latek:

pigor: ... , a może dla co niektórych np. tak , otóż dany odcinek AB o końcach A= (−5,2) i B=(3,−1) , czyli środku S=(−1,¹₂) tworzy wektor normalny AB^→= [8,−3] do szukanej symetralnej w punkcie S (lub jak kto woli kierunkowy tej symetralnej przez S) , wtedy załatwiamy problem jednym równaniem : 8(x+1)−3(y−¹₂)= 0 /*2 ⇔ 16x+16−6y+3= 0 ⇔ ⇔ 16x−6y+19= 0 − szukane równanie symetralnej odcinka AB ; −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− analogicznie dla odcinka AB , o końcach A=(1,6) i B=(4,−5), czyli S=(⁵₂,¹₂) i AB^→=[3,−11] mamy : 3(x−⁵₂)−11(y−¹₂)=0 ⇔ ⇔ 6x−30−22y+11= 0 ⇔ 6x−22y−19= 0 − szukane równanie symetralnej...

5-latek: Witam. Mozna . Tylko mialem dylemat czy to jest studentka czy uczennica . Wybralem to drugie −chociaz

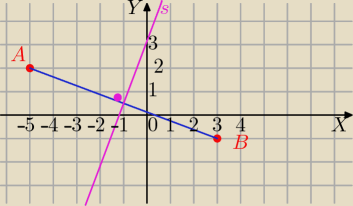
Mila: A=(−5,2) B=(3,−1) BEZENDU,11:23, (błędnie był zaznaczony punkt B, symetralna dobrze)

	8		19
s: y=		x+
	3		6

Inny sposób: Zastosowanie równania ogólnego prostej s: Ax+By+C=0 AB^→=[8,−3] to jest wektor prostopadły do symetralnej

	1
s: 8x−3y+C=0 i S=(−1,		)
	2

8*(−1)−3*0,5+C=0 −8−1,5+C=0⇔C=+9,5 s: 8x−3y+9,5=0

bezendu: faktycznie źle zaznaczone dziękuje za poprawienie

natalia: Wybaczcie ale to znowu ja ... Jestem uczennicą jak coś bo nie wiem czy to o mnie była mowa xD I nie ogarniam a mianowicie mam takie jedno fajne zadanie... Jakby ktoś je rozwiązał z dobrym tłumaczeniem byłabym bardzo znowu wdzięczna <3 Na prostej y=−3x+1 wyznacz punkt, którego odległość od punktu S=(2,1) równa jest 5.

Mila: Natalio, załóż nowy wątek.

jarek: wyznacz symetralno odcinka A i B , A[−3,7] i B[0,2]

Ola :-) :-): Witam, potrzebuje pomocy w zadaniu o treści : wyznacz równanie symetralnej odcinka o końcach A(−1,1) B(5,−1) to wazne.

Nikola : Witam potrzebuje pomocy a zadaniu. Napisz równanie symetralnej odcinka AB, jeśli A(−2,6) B (−3,−4)

Bogdan: Powtarzam mój wpis z 2010 r.

	x1 − x2
y = ax + b, a =		, y = a(x − x1) + y1 lub y = a(x − x2) + y2
	y1 − y2

Mila: II sposób Symetralna odcinka AB jest zbiorem wszystkich punktów płaszczyzny P(x,y) , takich, że: |AP|=|BP| A=(−2,6), B= (−3,−4) (x+2)²+(y−6)²=(x+3)²+(y+4)² wykonaj działania i uporządkuj