Równanie symetralnej odcinka Najt: Dane są punkty A=(3,6) i B=(2,8). Wyznacz równanie symetralnej odcinka AB. Prosiłbym o rozpisanie toku działania i użytych wzorów.

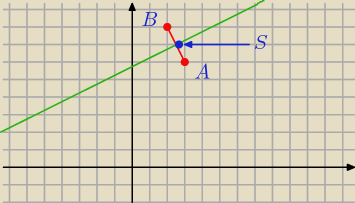
bezendu: A=(3,6) B=(2,8) prosta przechodząca przez te punkty 3a+b=6 /(−1) 2a+b=8 −3a−b=−6 2a+b=8 −a=2 a=−2 3*(−2)+b=6 −6+b=0 b=12 y=−2x+12

	3+2		6+8
środek odcinak |AB|=(		,		)
	2		2

S=(2,5; 7) prosta prostopadła do prostej y=−2x+12 i przechodząca przez punkt S −2*a=−1 −2a=−1

	1
a=
	2

	1
y=		x+b
	2

1
	*2,5+b=7
2

5
	+b=7
4

	5
b=7−
	4

	23
b=
	4

	1		23
prosta ta ma postać y=		x+
	2		4

Mila: II sposób: Symetralna odcinka jest zbiorem wszystkich punktów jednakowo odległych od końców odcinka. Niech P(x,y) należy do symetralnej AB A=(3,6) B=(2,8) wtedy: √(x−3)²+(y−6)²=√(x−2)²+(y−8)² równe odległości⇔ (x−3)²+(y−6)²=(x−2)²+(y−8)² x²−6x+9+y²−12y+36=x²−4x+4+y²−16y+64⇔ −6x+9−12y+36=−4x−16y+68⇔ 4y=2x+23

	1		23
y=		x+		równanie symetralnej AB
	2		4

bezendu: Mila pokazałbyś jak zrobić to na wektorach ?

mmk:

	5
S(		,7)
	2

symetralna s ⊥ pr AB i S€s

	8−6		1
wsp. kier. aAB=		= −2 , to as=
	2−3		2

	1
to: sym , s: y=		(x−xS)+yS
	2

	1		23
y=		x+
	2		4

bezendu: Dziękuje

Mila: Pokazałabym AB^→=[−1,2] równanie prostopadłej do AB^→ =[−1,2] w postaci ogólnej

	5
−1x+2y+C=0 prosta przechodzi przez punkt S=(		,7)⇔
	2

	5
−		+2*7+C=0
	2

11,5+C=0 C=−11,5 −x+2y−11,5=0 2y=x+11,5

	1		23
y=		x+
	2		4

bezendu: To jest z tego wzoru https://matematykaszkolna.pl/strona/1213.html i tego co jest w tablicach maturalnych ?

Grzegorz: A={х∊R:х²−2х−3=0}

5-latek: Zbior A = {−1, 3} Jest dwuelemtowy

Rafał: A=(−4,2) i B=(1,3)

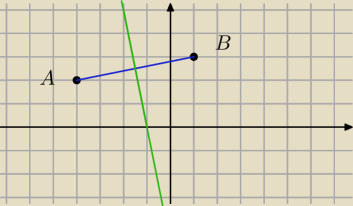
Qulka: symetralna y=−5x−5 (zielona)

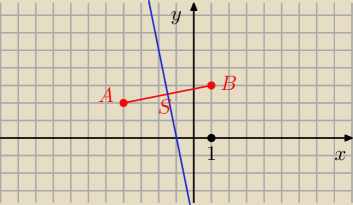
janek191: A = (x₁,y₁) = (−4,2) B = (x₂,y₂) = ( 1,3) S − środek odcinka AB

	x1 +x2		y1 + y2		3		5
S = (		,		) = ( −		,		)
	2		2		2		2

Prosta AB; y = a x + b

	y2 − y1		1
a =		=
	x2 − x1		5

a*a₁ = − 1

1
	*a1 = − 1 ⇒ a1 = −5
5

Symetralna y = a₁ x + k

	−3		5
y = −5 x + k S = (		,		)
	2		2

więc

5		−3
	= −5*(		) + k
2		2

k = − 5 Odp. y = −5 x − 5 ========================

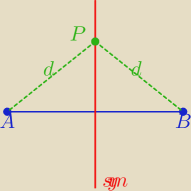
a@b: P(x,y) |AP|=|BP| = d (x+4)²+(y−2)²=(x−1)²+(y−3)² po wykonaniu działań i redukcji y= −5x−5 ==========

janek191: Eta ?

a@b: Co?