f.kwadratowa. Maleńka: Dany jest trójkąt ABC, gdzie A(−2,1) B(3,0), C(1,2) c) napisz równanie okręgu opisanego na trójkącie abc ... może mi ktoś wytłumaczyć jak się pisze takie równanie ? dziękuje z góry mam tyle ze r= |SB| = | SC| = |SA| można to zapisać jako √(3−a)2 + (0−b)2) = √(1−a)2 + (2−b)2 = √(−2−1)2 + (1−b)2 tylko że nie wiem czy to coś mi da.

Maleńka: może ktoś jednak pomoże ?

tom: poczekaj cos napisze...

bogumilll2: mi się zdaje że tu jest jakiś błąd

Maleńka: nie ma błędu .. tak jest w zadaniu. BC − to wysokość.. wynika to z podpunktu a) gdzie musiałam ją obliczyć.. ale problem mam tylko z c) ... i z następnymi zadaniami podobnymi do tego przez to także.. bo nie bardzo wiem jak takie równanie wyznaczyć.

Maleńka: dzięki Tom i czekam.

bogumilll2: aby wyznaczyc równanie okręgu trzeba znac współrzędne środka okręgu oraz długośc promienia r następnie podstawiasz do wzoru r=√(x−x_a)²+(y−y_a)² gdzie x_a i y_a są współrzędnymi środka okręgu.

Maleńka: a jak z trzech punktów A,B,C wyznaczyć środek okręgu

Maleńka:

Maleńka: ?

tom: środek odcinka AB toC'

	1
wektor AB=[5, −1] wektor AC'=		w.AB=[2,5 ; −0,5] C'=(0,5; 0,5)
	2

	1		3
prosta AB (z 1223) (3−2)(y−1)=(0−1)(x+2) czyli y=−		+		prosta k do niej
	5		5

prostopadła y=5x+b₁ ma przejść przez C' czyli 0,5=2,5 + b₁ b₁= −2 symetralna AB to y=5x−2

bogumilll2: jedynym sposobem jest wyznaczenie symetralnych odcinka i w ten sposób znalezienie środka okręgu

Maleńka: a takie coś √(3−a)²+(0−b)²=√(1−a)²+(2−b)² /² √(3−a)²+(0−b)²=√(−2−a)²+(1−b)² /² 9−6a+a²+b²=1−2a+a²+4−4b+b² 9−6a+a²+b²=4+4a+a²+1−2b+b² 9−6a=1−2a+4−4b 9−6a=4+4a+1−2b −4a+4b=−4 −10a+2b=−4 /(−2) −4a+4b=−4 20a−4b=8 16a=4 a=1/4 b=−3/4 r=√(3−a)²+(0−b)² r=√(9/4)²+(3/4)² r=√90/16 r=√45/8 równanie: (x−1/4)²+(y+3/4)²=45/8 dobrze?

tom: środek BC to A'

	1
wektor BC =[−2; 2] wektor BA'=		w.BC=[−1; 1] A'=(2; 1)
	2

prosta BC (1−3)(y−0)=(2−0)(x−3) y=−x+3 prosta l do niej prostopadła y=x +b₂ ma przejść przez A' czyli 1=2+b₂ b₂= −1 symetralna BC to y=x−1

Maleńka: r=√(3−a)²+(0−b)² r=√(9/4)²+(3/4)² r=√90/16 r=√65/8 równanie: (x−1/4)²+(y+3/4)²=65/8 pomyłka w liczeniu ale wyszło tak jak w książce i obyło się bez symetralnych ... dziękuję jednak za odpowiedz Tom. to mi się przyda

tom: pkt przecięcia symetralnych otrzymasz rozwiązując ukł. rownań y=5x−2 i y=x−1 wtedy

	1		3
S=(		; −		) − środek okręgu
	4		4

	11		3
promień jako długośc wektora np. →SB = [		;		]
	4		4

Maleńka: to jest do tego drugiego zadania

tom:

	1		3		130
równanie okręgu (x−		)2 + (y+		)2=
	4		4		16

Maleńka: a 130/16 to jest 65/8 ... wiec wyszło mi dobrze

Maleńka: a Tom.. jeśli chodzi o takie zadanie : Okrąg przechodzący przez punkt B (5,1) jest styczny do prostej k: x+y−2=0 w punkcie A(1,1) a) wyznacz równanie okręgu b) oblicz pole trójkąta CDS, gdzie S jest środkiem okręgu, zaś C i D są punktami przecięcia się parabli y= x2 − 2x z prostą k. tak krok po kroku ... proszę

tom:

Maleńka: bo tutaj nie wiem jak wyznaczyć te symetralne .. ewentualnie mogłabym coś pokombinować tak jak wcześniej ale sprzeczność mi wychodzi, albo coś knocę.

Maleńka: tak tak, tamto już rozumiem jak bede mieć podane na klasówce 3 punkty .. na pewno zrobię gorzej z tym następnym.

Maleńka: jak mam (5−a)² + (1−b)² = r² (1−a)² + ( 1−b)² = r² to 25−10a+a² + 1 − 2b + b² = 1−2a + a² + 1 −2b + b² czyli z tego wychodzi a=3 kiedy potem to podstawimy z a=3 wychodzi: 25−30+9+1−2b+b² = 1−6 + 9 + 1−2b + b² i wtedy wychodzi że 15−2b= 5−2b co jest totalna głupotą ....

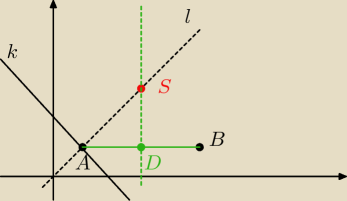
tom: środek okr. S leży na prostej l która jest prostopadła do danej prostej i przechodzi przez pkt styczności l: y=x i jednocześnie na symetralnej odcinka AB trzeba: −wyliczyć wektor AB −znaleźć wsp. pkt D ( wektor AD to połowa AB) −wyznaczyć prostą AB i prostą prostopadłą do niej przechodzącą przez D −pkt przecięcia ostatniej prostej i prostej l to S − promień to odl np SA

tom: takie zadania robi sie tak " jakbyś to rysowała" , krok po kroku, nie po omacku

Maleńka: D ( 4,1 ) .. to można odczytać z układu współrzędnych ale nie mam pojęcia jak wyznaczy prostą AB i prostą do niej prostopadłą przechodzącą przez punkt D .. mógłbyś mi coś napisać jeszcze

Maleńka:

tom: równanie prostej przechodzącej przez 2 pkty 1223

tom: pr. prostopadła do danej 42

tom: współrzędne pktu D nie odczytujesz a liczysz :z wektorów 1623

Maleńka: czyli prosta AB to będzie : (5−1)(y−1)=(1−1)(x−1) 4y−1=x−1 y=(−x)/4

Maleńka: halo halo ; d

tom: ^→_AB=[5−1; 1−1] = [4; 0]

	1
→AD=		→AB = [2; 0] stąd D=(3; 1)
	2

Maleńka: co do współrzędnych punktu D jestem w stanie odczytać dokłądnie z wykresu.. z osi ( 3,1).. a z tych wektorów wychodzi że AB= [4,0] .. wiec D by miało [2,1] ? bo nie rozumiem ... i w takim razie to by nie były współrzędne D.....

tom: nie pr AB to y = 1

Maleńka: ok − rozumiem.. a to : (5−1)(y−1)=(1−1)(x−1) 4y−1=x−1 y=(−x)/4 było dobrze

Maleńka: no tak y=1 ... to widać z wykresu .. w takim razie nie powinnam tamtego wyliczać ? gubię się..

tom: (5−1)(y−1) = (1−1)(x−1) 2y−2= 0*(x−1) czyli y = 1

Maleńka: WIDZĘ BLĄD W OBLICZENIACH. TAK .. z tego wzoru wychodzi,że y=1

Maleńka: hahaha : ) prześcignąłeś mnie : ) i co teraz na sam koniec

tom: symetralna AB ma wzór x=3

Maleńka: −pkt przecięcia ostatniej prostej i prostej l to S czyli z tej prostopadłej co mi wysłałeś stronę. już liczę

Maleńka: skąd wiesz,że ma taki wzor

Maleńka: z rynku ?

tom: układ równań x=3 i y=x stąd y=3

Maleńka: ab to było że y=1 tutaj mamy x=3 ... czyli y=3 czyli że a1 razy a2 = 3

Maleńka: ?

tom: niefortunnie sie złożyło , wzory ze str 42 sa dla a≠0

tom: co to a1 i a2

Maleńka: a wiec jakie będą dla a=0 ?

Maleńka: a1 , a2 .. to z tego wzoru było dla a≠0 :(

tom: środek okręgu ma współrzędne (3; 3) promień z odległości punktów np. AS |AS|² = (3−1)² + (3−1)² czyli |AS| = r = 2√2 równanie okręgu (x−3)² + (y−3)² = 8

Maleńka: skąd wiesz,że ma takie współrzędne ? jak to "obliczyles"

tom: 1468

Maleńka: ................ ale my nie mamy a i b.. znaczy jakie a i b... bo w tym można się pogubić.

Maleńka: chodzi mi o to S(3,3) a nie o to jak wyliczyłeś r...

Maleńka: mi wyszło że |AS| = 2 .. A nie 2√2

Maleńka: 9−7 + 9−7 = |as|² 4=|as|²

tom: wybacz, widać niewiele umiesz ( bez urazy ) spójrz na rysunek S jest punktem przecięcia prostej l i symetralnej odcinka AB jego współrzędne to współrzędne (a,b) na 1468

Maleńka: no racja − nie umiem wiele.. te tematy nie są wcale łatwe a do tego nie przerobione w szkole ja wiem że to jest to a..b ; ) odkryłam sama ; d hehehe ale ........ my nie wiemy jakie jest to a i b......

Maleńka: ty nie wiesz tego ze istnieje takie cos jak (x−3)² + (y−3)² = 8 ............. żeby to napisać musisz znać S. a S napisałeś że ma (3,3) i w Twojej wypowiedzi nie widzę objaśnienia skąd − a o to pytałam. przepraszam,że tak męczę....

tom: nie mam siły okrąg o środku S(a,b) i promieniu r ma równanie (x−a)² + (y−b)² =r² wyszło że S =(3,3) a r=2√2 gdzie problem

Maleńka: hahaha ; d problem w tym skąd wyszło to że s = (3,3)

Maleńka: musisz znaleźć siłę, wierze w Ciebie ! hehehe

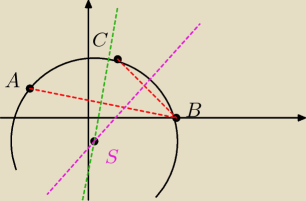
Maleńka: apropo zaczęłam robić podpunkt b) i tak ; d mamy : y=x²−2x Δ=4 √Δ = 2 x1= (2−2)/2 x1=0 x2= (2+2)/2 x2=2 P( −b/2a , −Δ/4a) P = ( 1, −1) te czerwone to C i D. S powinnam umiescic z poprzeniego zadania jako (3,3) ?

Maleńka: Okrąg przechodzący przez punkt B (5,1) jest styczny do prostej k: x+y−2=0 w punkcie A(1,1) a) wyznacz równanie okręgu b) oblicz pole trójkąta CDS, gdzie S jest środkiem okręgu, zaś C i D są punktami przecięcia się parabli y= x2 − 2x z prostą k. takie bylo polecenie..

Maleńka: i w ogóle to jesteś cudowny i dziękuję!

tom: nalezy rozwiązać układ równan y=x² − 2x i x + y − 2 = 0 y = −x+2 podstawiam −x+2=x²−2x czyli x²−x−2=0 √Δ=3 x₁=−1 x₂ = 2 y₁=3 y₂= 0 czyli C=(−1; 3) D=(2; 0)

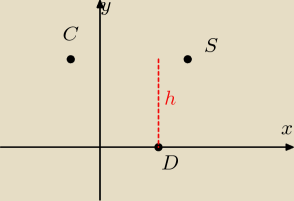
tom: widać ze ^→_CS= [4; 0] więc |CS|=4 h = 3 wysokość Δ

	1
pole PΔ=		|CS| h = 6
	2

Maleńka: dziękuję