Okrąg i dwie proste styczne
PR7: Znajdź równanie okręgu stycznego do prostej k: x+y+13=0 i do prostej m: 7x−
y−5=0 w punkcie A(1,2)
Proszę wyrozumiałość i przeczytanie tego oraz o szczegółowe rozpisanie, będę naprawdę
wdzięczny!
nie chce mi to zadanie wyjść − rozwiązałem już kilka takich zadań tylko
że okrąg miał przechodzić przez albo początek układu ( i tutaj styczne albo były równoległe,
prostopadłe albo
po prostu się przecinały ), albo przez dany punkt ale żadna prosta przez niego nie przechodzi
− i to mi wychodzi
natomiast tutaj gdzieś mam błąd.
zadania które zrobiłem :
https://matematykaszkolna.pl/forum/408721.html ;
https://matematykaszkolna.pl/forum/190719.html ;
https://matematykaszkolna.pl/forum/408746.html ;
Próbowałem robić tak jak robią to ICSP i Mila powyżej, lecz na tej stronie, autor robi to
całkiem inaczej,
czyli wyznacza prostą prostopadłą do prostej która zawiera punkt A, tzn nie szuka
dwusiecznej...
(mowa o stronie :
https://zadania.info/d279/1238943 )
czy da się to zrobić tak jak w tych sposobach ICSP i Mila? Bo tutaj mi nie wychodziło to :
|x+y+13|/{2} = |7x−y−5|/5{2}
stąd mi wyszły dwie dwusieczne kątów jakie tworzą te proste (jedną odrzucamy i zostawiamy tą o
równaniu
y = −3x−15 bo to na niej jest okrąg ), więc okrąg szukany ma środek S(xs,−3xs−15)
następnie próbowałem obliczyć promień lecz chyba tutaj popełniłem błąd, bo przyjąłem że okrąg
przechodzi
przez punkt (0,0) − tutaj podstawiłem za "y" : −3x−15, bo wtedy xs
2+ys
2=r
2, więc mam
równanie kwadr. z jedną
niewiadomą
{xs
2+(−3xs−15)
2} = |xs+(−3x−15)+13|/{2}
{xs
2+9xs
2+90xs+225} = |xs−3xs−2|/{2}
stąd mi wyszło
16xs
2+172xs+446=0
xs1=...
xs2=...
i następnie dwa okręgi o środkach (xs1,ys1) i (xs2,ys2) − "ys1 i ys2" obliczyłem podstawiając
kolejno x1 i x2
do równania dwusiecznej y=−3x−15
i stąd następnie obliczyłem promień dla tych okręgów
(xs1)
2+(ys1)
2=r
2
oraz dla drugiego okręgu
(xs2)
2+(ys2)
2=r
2 i faktycznie sprawdzając na kalkulatorze graficznym te okręgi są styczne do
dwóch prostych k i m oraz przechodzą przez początek układu, ale teraz jak zrobić to dla punktu
(1,2)?
Próbowałem też od momentu ( cofając się ) gdy miałem równanie dwusiecznej na której leży środek
okręgu
policzyć to właśnie nie dla punktu (0,0) tylko (1,2) i miałem
{(1−xs)
2+(2−(−3x−15)
2} = |xs−3xs−2|/{2}
xs1=... , ys1=...
xs2=..., ys2=...
a następnie obliczyłem dla nich promienie r = {(1−xs)
2+(2−ys)
2} ...
i wtedy wyznaczając równania tych okręgów faktycznie przechodziły przez punkt (1,2) lecz już
nie były
styczne do prostej k i m, tzn przecinały je dwa razy. Proszę o wytłumaczenie tego.
30 mar 19:46
Qulka: zaczął od prostej prostopadłej, bo wyjątkowo masz już punkt styczności więc nie trzeba
kombinować i go szukać
a promień jest prostopadły do stycznej
30 mar 19:53
Qulka:
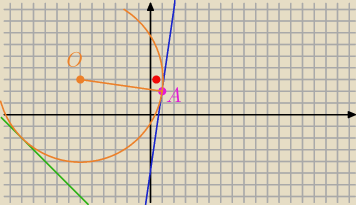
(x+6)
2+(y−3)
2=50
30 mar 19:56
PR7: ale są dwa takie okręgi ( dwa przypadki )
30 mar 20:12
Qulka: drugi mi się nie zmieścił na obrazku

30 mar 20:13
Qulka: ale analogicznie tylko w dół ... odmierzasz 10 przekątnych od przecięcia zielonej z niebieską i
znów rysujesz proste prostopadłe
30 mar 20:15
PR7: czyli tutaj nie da się tego obliczyć takimi sposobami jak w tych linkach z matematykaszkolna pl
?
30 mar 20:17
PR7: ale analogicznie tylko w dół ... odmierzasz 10 przekątnych od przecięcia zielonej z niebieską i
znów rysujesz proste prostopadłe
przekątynych?
30 mar 20:18
Qulka: jak masz już punkt styczności to po co wyważać otwarte drzwi

30 mar 20:18
Qulka: bo odległość 10√2 to po prostu 10 przekątnych licząc po kratkach (zielona to prosta pod
kątem 45° biegnąca po przekątnych)
30 mar 20:20
PR7: tzn dlaczego mi to nie chce wyjść podstawiając nie tak jak autor w tym linku
https://zadania.info/d279/1238943
że 7y=−x+15 i
wtedy środek (−7y+15,y) tylko tak jak ja robiłem czyli podstawiając dwusieczną y=−3x−15 czyli
S(x,−3x−15) to nie chce wyjść? Albo
jeśli da się to mogłabyś to rozwiązać proszę
30 mar 20:21
chichi:
Już byś chciał schematem lecieć... usiądź pomyśl chwilę... Promień poprowadzony do punktu
styczności jest prostopadły do ów stycznej, przecież to jest wiedza z poziomu podstawowego

30 mar 20:25
Qulka: bardziej dookoła to się chyba nie dało

jak masz dwusieczną to znajdź jej punkt przecięcia z prostą prostopadłą do danej przechodzącą
przez A i będzie dobrze
30 mar 20:25
PR7: usiądź pomyśl chwilę − siedzę nad tym już 5 godzin... a matmę super ogarniam tylko że tego
teraz w 2
liceum jeszcze nie brałem

No dobra czyli mamy układ równań
y=−3x−15
7y=−x+15
stąd S1(−6,3)
|S1A|
2 = (−6−1)
2+(3−2)
2 = 50
czyli mam równanie pierwszego okręgu
(x+6)
2+(x−3)
2=50
a teraz idąc tą metodą jak wyznaczyć równanie drugiego?
bierzemy wtedy pod uwagę drugą dwusieczną czyli
7y+−x+15
6y−2x+70=0
stąd S2(29,−2) no i promień r
2 = 800 czyli
(x−29)
2+(y+2)
2=800

30 mar 20:39
PR7: a teraz idąc tą metodą jak wyznaczyć równanie drugiego?
bierzemy wtedy pod uwagę drugą dwusieczną czyli
7y=−x+15
6y−2x+70=0***
30 mar 20:39
Qulka: drugi ma (x−29)2+(y+2)2=800
30 mar 20:48
Qulka: tak ten układ równań rozwiąż
30 mar 20:48
PR7: czyli dobrze zrobiłem − chyba strona się sama nie odświeża i nie widziałaś że napisałem −
dzięki za pomoc <3
30 mar 20:53
Mila:
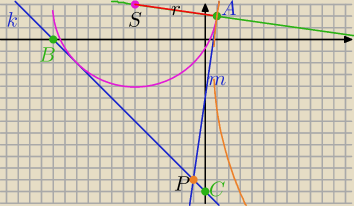
Okrąg styczny do prostej
k: x+y+13=0 i do prostej
m: 7x−y−5=0 w punkcie A(1,2)
1) promień jest prostopadły do prostej m w p. A
n− prosta prostopadła do m i A∊n
n: x+7y+C=0 i 1+7*2+C=0 ⇔C=−15
n: x+7y−15=0 ⇔x=−7y+15
S=(a, b) leży na prostej n⇔S=(−7y+15, y) i |AS|=r=
√(−7b+15−1)2+(b−2)2
|AS|=√50*(b−2)2=√50*|b−2|=r
3) Odległość S (a,b) od prostej k jest równa |AS|
| |−7b+15+b+13| | |
| =√50*|b−2| |
| √2 | |
|−6b+28|=
√100*|b−2|
−6b+28=10(b−2) lub −6b+28=10*(2−b)
b=3 lub b=−2
S=(−7*3+15, 3)=(−6,3) i r
2=50*(3−2)
2=50 stąd (x+6)
2+(y−3)
2=50
[ okrąg wpisany w kąt APB ]
lub
S=(−7*(−2)+15,−2)=(29,−2) i r
2=50*(−2−2)
2=50*16=800
stąd
(x−29)
2+(y+2)
2=800
okrąg wpisany w kat APC
30 mar 21:16
Mila:
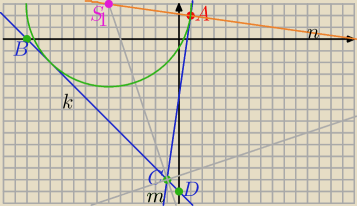
Okrąg styczny do prostej
k: x+y+13=0 i do prostej
m: 7x−y−5=0 w punkcie A(1,2)
II sposób − dwusieczne kątów między prostymi:
P(x,y)− punkt należący do dwusiecznej
| | |x+y+13| | | |7x−y−5| | |
1) |
| = |
| ⇔ |
| | √2 | | √50 | |
5|x+y+13|=|7x−y−5|⇔
5(x+y+13)=7x−y−5 lub 5(x+y+13)=−7x+y+5
Równania dwusiecznych:
x−3y−35=0 lub 3x+y+15=0
2) S=(a,b) leży na dwusiecznej kąta BCA lub dwusiecznej kąta ACD
SA⊥m w punkcie styczności A
n− prostopadła do m
n: x+7y−15=0
Przecięcie prostej n z dwusiecznymi wyznaczą środki okręgów stycznych do prostych
i przechodzących przez p. A
a) x+7y=15 i 3x+y=−15
S
1=(−6,3) i |S
1A|
2=50=r
2
lub
x+7y=15
x−3y=35
S
2(29,−2) nie mieści się na rysunku
|S
2A|
2=800=r
2
cd. jw.
30 mar 22:33
PR7: Dobra tak jak liczyłem na samym samym początku też by wyszło tylko walnąłem
Się rachunkowo i wtedy mamy dwa równania
| Okrąg
Dla pierwszej dwusiecznej y=−3x−15
{(x−1)²+(2−(−3xs−15))2} = |x+(−3x−15)+13|/ {2}
I stąd wyjdzie x= −6, y= −3*(−6)−15= 3 , no i jeszcze promień − |SA|...= ✓50 = 5✓2
(x+6)²+(y−3)²= 50
Oraz dla drugiej dwusiecznej x=3y+35 , S(3y+35,y)
|| Okrąg
{(1−(3y+35))²+(2−y)²} = |(3y+35)+y+13|/ {2}
Stąd y = −2, czyli x= 3*(−2)+35= 29 no i potem jeszcze promień
Jako odległość środka od punktu A... = ✓800
(x−29)²+(y+2)² = 800
no i wyszło to samo, czyli mamy zrobione to zadanie na 4 sposoby heh
31 mar 06:54
PR7: Dla pierwszej dwusiecznej y=−3x−15
{(x−1)²+((−3xs−15)−2)²} = |x+(−3x−15)+13|/ {2} *** chociaż tutaj jest wyrażenie ()², ale
już poprawię do perfekcji
31 mar 07:09
 (x+6)2+(y−3)2=50
(x+6)2+(y−3)2=50



 jak masz dwusieczną to znajdź jej punkt przecięcia z prostą prostopadłą do danej przechodzącą
przez A i będzie dobrze
jak masz dwusieczną to znajdź jej punkt przecięcia z prostą prostopadłą do danej przechodzącą
przez A i będzie dobrze
 No dobra czyli mamy układ równań
y=−3x−15
7y=−x+15
stąd S1(−6,3)
|S1A|2 = (−6−1)2+(3−2)2 = 50
czyli mam równanie pierwszego okręgu
(x+6)2+(x−3)2=50
a teraz idąc tą metodą jak wyznaczyć równanie drugiego?
bierzemy wtedy pod uwagę drugą dwusieczną czyli
7y+−x+15
6y−2x+70=0
stąd S2(29,−2) no i promień r2 = 800 czyli
(x−29)2+(y+2)2=800
No dobra czyli mamy układ równań
y=−3x−15
7y=−x+15
stąd S1(−6,3)
|S1A|2 = (−6−1)2+(3−2)2 = 50
czyli mam równanie pierwszego okręgu
(x+6)2+(x−3)2=50
a teraz idąc tą metodą jak wyznaczyć równanie drugiego?
bierzemy wtedy pod uwagę drugą dwusieczną czyli
7y+−x+15
6y−2x+70=0
stąd S2(29,−2) no i promień r2 = 800 czyli
(x−29)2+(y+2)2=800 
 Okrąg styczny do prostej
k: x+y+13=0 i do prostej
m: 7x−y−5=0 w punkcie A(1,2)
1) promień jest prostopadły do prostej m w p. A
n− prosta prostopadła do m i A∊n
n: x+7y+C=0 i 1+7*2+C=0 ⇔C=−15
n: x+7y−15=0 ⇔x=−7y+15
S=(a, b) leży na prostej n⇔S=(−7y+15, y) i |AS|=r=√(−7b+15−1)2+(b−2)2
|AS|=√50*(b−2)2=√50*|b−2|=r
3) Odległość S (a,b) od prostej k jest równa |AS|
Okrąg styczny do prostej
k: x+y+13=0 i do prostej
m: 7x−y−5=0 w punkcie A(1,2)
1) promień jest prostopadły do prostej m w p. A
n− prosta prostopadła do m i A∊n
n: x+7y+C=0 i 1+7*2+C=0 ⇔C=−15
n: x+7y−15=0 ⇔x=−7y+15
S=(a, b) leży na prostej n⇔S=(−7y+15, y) i |AS|=r=√(−7b+15−1)2+(b−2)2
|AS|=√50*(b−2)2=√50*|b−2|=r
3) Odległość S (a,b) od prostej k jest równa |AS|
 Okrąg styczny do prostej
k: x+y+13=0 i do prostej
m: 7x−y−5=0 w punkcie A(1,2)
II sposób − dwusieczne kątów między prostymi:
P(x,y)− punkt należący do dwusiecznej
Okrąg styczny do prostej
k: x+y+13=0 i do prostej
m: 7x−y−5=0 w punkcie A(1,2)
II sposób − dwusieczne kątów między prostymi:
P(x,y)− punkt należący do dwusiecznej