wyznacz równanie okręgu Kasia: Wyznacz równanie okręgu stycznego jednocześnie do dwóch prostych o równaniach x+y−3=0 i x+y+5=0 oraz przechodzącego przez punkt P(√7;0) Wyznaczyłam prostą, na której ma się znajdować środek okręgu, czyli równoległa do pozostałych i oddalona o tyle samo. y=−x−1. Czyli środek okręgu ma być w jakimś punkcie (t: −t−1). Wiem, że należy teraz wyznaczyć promień, czyli odległość punktu od prostej. I tu utknęłam. Jakieś wskazówki proszę?

Dominik: odleglosc miedzy prostymi wynosi 2r

	|−3 − 5|
2r =		= 4√2
	√2

r = 2√2

Buka: Ok. Ale to się wzięło ze wzoru na odl. punktu.. Ale jak podstawiam przykładowo P (0,3) przez który przechodzi pierwsza prosta i od ma być oddalony od tej prostej między tymi dwoma, czyli prostej −x−y−1=0, nie wychodzi mi coś takiego. Skąd −3 i −5?

Dominik: odleglosc miedzy prostymi rownoleglymi Ax + By + C₁ = 0, Ax + By + C₂ = 0 wyraza sie wzorem d

	|C1 − C2|
=
	√A2 + B2

Buka: Ahhh. Okej. Faktycznie, jest taki wzór. Ale co teraz zrobić, żeby wyznaczyć całe równanie? promień mam. Nie mam środka..

Dominik: srodek okregu ma wspolrzedne S = (x, −x + 1) (bo lezy na prostej y = −x + 1 stad √x² + (−x + 1)² = √x² + x² + 1 − 2x = √2x² − 2x + 1 = r √2x² − 2x + 1 = 2√2 stad otrzymujesz x, dalej podstaw x do y = −x + 1 i masz wspolrzedne srodka okregu oraz promien

Dominik: lezy na prostej y = −x − 1, popraw blad i powinno wyjsc OK

BlondynA i Zen64 i Andriej:

⎧	(3−y−a)2+(y−b)2=r2
⎨	(−5−y−a)2+(y−b)2=r2
⎩	y=0

czyli (3−a)²=(−5−a)²,czyli 3−a=5+a,skończ sama! a−wspólrzędna X środka okręgu

Dominik: aj, nie wiem co tam stworzylem. √(x − √7)² + (−x + 1)² = 2√2 z tego wyznacz x i dalej jak pisalem. oczywiscie to sie bierze ze wzorku na odleglosc pktu (x, −x + 1) od (√7, 0) (wynosi on r)

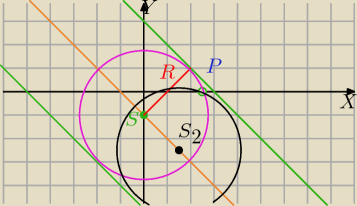
Mila: x+y−3=0 i x+y+5=0 oraz przechodzącego przez punkt P(√7;0) k: x+y−3=0 y=−x+3 m: x+y+5=0 y=−x−5 m||k n: y=−x+b prosta równoległa do prostych mi k i równo od nich oddalona

	3+(−5)
S=(0,ys) ys=		=−1
	2

n: y=−x−1 środek okręgu stycznego do obu prostych leży na prostej y=−x−1 R − odległość punktu S od prostej y=−x+3

	|0+(−1)−3|		4
R=		=		=2√2
	√12+12		√2

O(a,b)=(a,−a−1) Równanie okręgu; P=(√7,0)∊okręgu (x−a)²+(y−(−a−1))²=(2√2)²⇔(√7−a)²+(a+1)²=8⇔2a²+2a−2√7a=0 a=0 lub a=√7−1≈ b=−0−1=−1lub b=−√7 S₁=(0,−1) i s₂=(√7−1,−√7) równania okręgów x²+(y+1)²=8 (x−√7+1)²+(y+√7)²=8

Buka: Dziękuję Wam bardzo za pomoc! wszystko wyszło, po godzinach pracy. haha

Mila: to miło, że zauważyłaś rozwiązanie.