Okrąg i styczne PR7: Napisz równanie okręgu przechodzącego przez początek układu współrzędnych i stycznego do prostych x+2y+9=0 oraz 2x−y−2=0.

ICSP: https://matematykaszkolna.pl/forum/408721.html

PR7: właśnie widziałem to i siedziałem nad tym 2h i mi nie wychodzi

PR7: jakby nie patrzeć to nie otrzymasz od razu równania dwusiecznej, bo niewiadome się nie skrócą

ICSP: dwusieczna nie musi być prostą pionową lub pozioma. Może być też w postaci: y = ax + b

chichi: Ale o jakim skracaniu ty mówisz? Proste z zadnia podesłanego przez @ICSP się różnią, on pokazał Ci tylko analogiczne rozwiązanie, na którym możesz się wzorować. W tamtym zadaniu oba równania dwusiecznych zaproponowanych przez @Mila są poprawne

PR7: Dobra na razie otrzymałem −x+3y+11=0 lub 3x+y+7=0 i teraz odrzucamy prostą −x+3y+11=0 bo nie spełnia warunków zadania czyli zostaje y= −3x−7

PR7: @ICSP wiem...

ICSP: Czyli środek okręgu ma współrzędne: (x , −3x − 7)

	|x + 2(−3x − 7) + 9|
|SO| = √x2 + (3x + 7)2 = r =
	√5

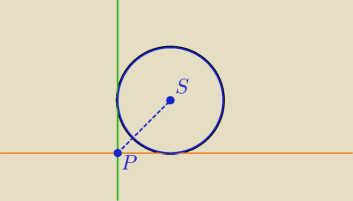
chichi: Zauważ, że zadane proste w poleceniu są wzajemnie prostopadłe więc otrzymamy drugie równanie, a więc po kolei: O: (x−a)²+(y−b)²=r², S=(a, b), R=(0,0) (1) R∊O ⇒ a²+b²=r² (2) Równanie dwusiecznej: y=−3x−7 (3) Korzystam z (1) i mam: x₀²+(−3x₀−7)²=r² (4) P=(−1, −4) (5) |SP|²=2r² ⇒ (x₀+1)²+(−3x₀−3)²=2r² (6) Z (3) i (5) mamy: (x₀+1)²+(−3x₀−3)²=2(x₀²+(−3x₀−7)²) Dalej już sam dokończ, to równanie kwadratowe P.S. Rysunek jest poglądowy, aby zauważył skąd wziął się punkt (5)

chichi: Powinieneś otrzymać takie równania okręgów: O₁: (x+2)²+(y+1)²=5

	22		31		289
O2: (x+		)2+(y−		)2=
	5		5		5

PR7: już rozumiem − dzięki wielkie!

Filip: bardzo zobry rysunek

PR7: wcześniej rozwiązałem tak jak ICSP tylko minusa zgubiłem, więc jeszcze przed tym moim wpisem na forum doszedłem do rozwiązania ( i otrzymałbym identyczne dwa równania okręgów, tylko minusa zgubiłem pod sam koniec...), ale nie rozumiem nadal w twoim sposobie @chichi ( który się bardzo nie różni ) dlaczego długość SP to 2r²? Chodzi tutaj o przekątną kwadratu a następnie ², tak?

ICSP: |SP| = √r² + r² = √2r − długość SP |SP|² = 2r²

PR7: no to czyli z przekątnej kwadratu o boku r... nie łatwiej tak napisać? ICSP Dzięki jeszcze raz

PR7: Można też ułożyć równanie dla S(a, −3a−7) jako równanie okręgu leżącego na dwusiecznej y = −3x−7 i stycznego do jednej z tych prostych ( tylko tutaj promień może być równy tylko i wyłącznie odległości środka od punktu (0,0), bo jeśli się napisze że r = odległości środka od jednej z prostej do której jest styczny to wyjdzie x ∊ R ) (x−a)² + (2x−2−(−3a−7))² = a²+(−3a−7)² (x−a)² + (2x+3a+5))² = a²+(3a+7)² i stąd po podniesieniu ()² mamy 5x²+(20+10a)x−24−12a = 0 skoro ma być do tej prostej styczny to Δ = 0, zatem Δ = 0 ⇔ 100a²+640a+880 = 0, stąd a = ⁻²²₅ lub a = −2, czyli mamy to samo, teraz jeszcze tylko podstawić do b = −3a−7 żeby obliczyć "b", b = 1 lub b = ³¹₅ no i potem jeszcze promień

PR7: ...żeby obliczyć "b", b = −1***