Okrąg i styczne Werka: Cześć! Mam takie zadanie: Ułóż równanie okręgu, który jest styczny do dwóch prostych 2x+y−1=0 i 2x−y+2=0 i przechodzi przez początek układu współrzędnych. Próbowałam już wiele razy podejść do tego zadania, ale mi nie wychodzi. Jedyna sensowna rzecz, do której doszłam to c=0, bo (0−a)²+(0−b)²=a²+b²−c Macie jakieś wskazówki?

Filip: @chichi / @chichi

Chińska podróba 6-latka: znajdź równanie dwusiecznej kąta ostrego między tymi prostymi

ICSP: Czym jest c? (x−a)² + (x−b)² = r² a² + b² = r² okrąg ma równanie: (x−a)² + (x−b)² = a² + b² S(a,b) , r² = a² + b² Masz punkt S(a,b) którego odległość od prostych 2x + y − 1 = 0 , 2x − y + 2 = 0 jest równa √a² + b² Po podstawieniu do odpowiedniego wzoru i porównaniu powinnaś otrzymać: |2a + b − 1| = |2a − b + 2| skąd

	1		−3
a = −		i b =		± √5/8
	4		8

chichi: Dobrze przepisałas te równania prostych? Bo aż się proszą żeby być równoległe

Werka: @chichi tak, na pewno dobrze

Werka: @ICSP dziękuję! Czy mógłbyś mi wytłumaczyć skąd wziąłeś to b? To niestety nadal mi nie wychodzi, a mam

ICSP: z równania:

	|2a + b − 1|
√a2 + b2 =
	√5

powinnaś je kiedyś dostać podczas swoich wyliczeń.

Werka: Dziękuję i pozdrawiam!

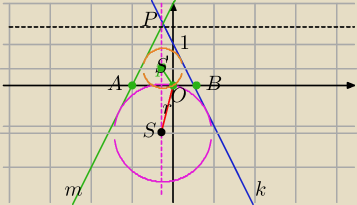
Mila: 2x+y−1=0 i 2x−y+2=0 ⇔ k: y=−2x+1 m: y=2x+2 1) środek okręgu wpisanego w kąt leży na dwusiecznej tego kąta. (0,0)∊okręgu S=(a,b)− wsp. środka okręgu a²+b²=r² 2) P=(x,y) − punkt należący do dwusiecznej kąta APB

|2x+y−1|		|2x−y+2|
	=
√5		√5

|2x+y−1|=|2x−y+2|

	3
2x+y−1=2x−y+2⇔y=		− ta dwusieczna nie odpowiada war. zadania
	2

lub 2x+y−1=−2x+y−2 4x=−1

	1
x=−		− druga dwusieczna , na tej dwusiecznej leży środek okręgu wpisanego w kąt ABP
	4

	1
S=(−		, b)
	4

	1   |2*(− )+b−1|   4
|SO|=√(1/4)2+b2=
	√5

5		3
	+5b2=|b−		|2
16		2

b jak u ICSP 2 rozwiązania

	1		3
S=(−		,−		−√(5/8))
	4		8

	1		3
S'=(−		,−		+√(5/8))
	4		8