.
Grzes:
Zad.3. Punkty A=(3,1) , B=(6,6), C=(4,8) D=(−2,−2)są wierzchołkami trapezu ABCD.
Wiedząc, że AB i CD są równoległe, oblicz pole tego trapezu .
29 mar 12:00
Konrad: P trapezu=(a+b)*h/2
29 mar 12:06
chichi:
Wyznacz równanie prostej AB, policz odległość punktu C od prostej AB, policz |AB| i |CD|, a na
koniec podstaw do wzoru na pole

29 mar 12:06
Grzes: A równania prostej AB czyli
29 mar 12:07
ICSP: Wyznacz:
1
o Długość odcinka AB =a
2
o Długość odcinka CD = b
3
o Równanie prostej AB
4
o Odległość punktu C od prostej AB = h
29 mar 12:07
Grzes: ICSP pomoglabys?
29 mar 12:09
Grzes: Ważne, proszę
29 mar 12:10
29 mar 12:10
getin:
|AB| =
√(6−3)2+(6−1)2 =
√9+25 =
√34
|CD| =
√(8+2)2+(4+2)2 =
√100+36 =
√136 =
√4*34 = 2
√34
prosta AB: y = ax+b
{6 = 6a+b
{1 = 3a+b
6−6a = 1−3a
−3a = −5
1 = 5+b
b = −4
3y = 5x−12
5x−3y−12 = 0 − prosta AB
h = odległość punktu C=(4,8) od prostej 5x−3y−12=0 czyli od prostej AB
| | |5*4−3*8−12| | | |20−24−12| | | 16 | |
h = |
| = |
| = |
| |
| | √52+(−3)2 | | √34 | | √34 | |
| | a+b | | √34+2√34 | | 16 | | 3√34 | | 16 | |
P = |
| *h = |
| * |
| = |
| * |
| = 8 |
| | 2 | | 2 | | √34 | | 2 | | √34 | |
29 mar 12:11
getin:
wróć, pole to oczywiście 24 a nie 8
29 mar 12:13
mam pytanie: AB=√34 (można też z tw. Pitagorasa odczytując długości odpowiednich trójkątów prostokątnych z
rysunku, ale to metoda chyba dla szkoły podstawowej raczej)
CD=2√34
prosta CD y=ax+b
−2=−2a+b
8=4a+b
y=5/3x+4/3 czyli 5/3x−y+4/3=0
h=8/√34
PTRAPEZU=3√34/2*8/√34=12
29 mar 12:39
mam pytanie: u mnie pewnie błąd
29 mar 12:40
getin:
h = 16/√34
29 mar 12:42
Saizou :
Wierzchołki są punktami kratowymi, zatem ze wzoru Picka mamy
W = 22 (punkty kratowe leżące wewnątrz wielokąta)
B = 6 (punkty kratowe leżące na brzegu wielokąta)
| | 6 | |
P = 22 − |
| + 1 = 22+3−1 = 24 |
| | 2 | |
29 mar 12:53
circle:
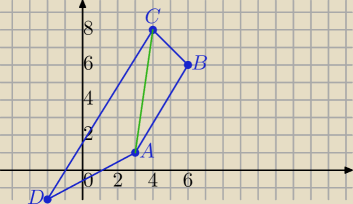
Punkty A=(3,1) , B=(6,6), C=(4,8) D=(−2,−2) są wierzchołkami trapezu ABCD.
Wykorzystamy wektory i wyznaczniki.
1)
BC
→=[−2,2],
BA
→=[−3, −5]
| | 1 | |
PΔABC= |
| |(−2)*(−5)−2*(−3)|= |
| | 2 | |
2)
DA
→=[5,3]
DC
→=[6,10]
3)
P
ABCD=8+16=24
29 mar 17:32

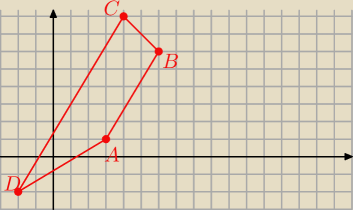 1. liczymy długość odcinka AB i CD
https://matematykaszkolna.pl/strona/1248.html
2.liczymy wysokość trapezu (najpierw równania prostej CD, potem odległość punktu a od prostej
CD)
https://matematykaszkolna.pl/strona/1223.html
https://matematykaszkolna.pl/strona/1249.html
3. liczymy pole trapezu
1. liczymy długość odcinka AB i CD
https://matematykaszkolna.pl/strona/1248.html
2.liczymy wysokość trapezu (najpierw równania prostej CD, potem odległość punktu a od prostej
CD)
https://matematykaszkolna.pl/strona/1223.html
https://matematykaszkolna.pl/strona/1249.html
3. liczymy pole trapezu
 Punkty A=(3,1) , B=(6,6), C=(4,8) D=(−2,−2) są wierzchołkami trapezu ABCD.
Wykorzystamy wektory i wyznaczniki.
1)
BC→=[−2,2],
BA→=[−3, −5]
Punkty A=(3,1) , B=(6,6), C=(4,8) D=(−2,−2) są wierzchołkami trapezu ABCD.
Wykorzystamy wektory i wyznaczniki.
1)
BC→=[−2,2],
BA→=[−3, −5]