Pomóżcie z planimetrii tak, żeby mi wytłumaczyć, nie zrobić <3 Oskar: 1. Pole równoległoboku wynosi 54, a kąt ostry ma miarę 30. Stosunek boków wynosi 4:3, wyznacz ich długości. 2. Długość przekątnej kwadratu jest o 3 większa od długości jego boku. Oblicz pole tego kwadratu. 3. W trójkącie ABC dane są: długość AC = 4√2cm oraz miary kątów CBA i CAB są równe odpowiednio 30* i 45*. Oblicz długość boku BC. 4. Przekątna AC prostokąta ABCD jest o 2 dłuższa od jednego z boków, drugi bok wynosi 10. Oblicz długości boków. 5. Dany jest trójkąt ABC, w którym AC=BC, kąt < ACB = 80 zaś AD jest dwusieczną kąta BAC i D (euro) BC. Wyznacz miarę kąta ADB. 6. Obwody trójkątów podobnych wynoszą odpowiednio 8 i 2√2. Skala podobieństwa jest równa? Sorrki, że tyle zadań ale koronaferie i nauczyciele nie mają jak nam tego wytłumaczyć dlatego liczę, że ktoś z was mi pomoże zrozumieć planimetrie

a7: a która klasa ,żeby dostosować się z tłumaczeniem?

Oskar: 4 technikum ale celującym uczniem nie jestem

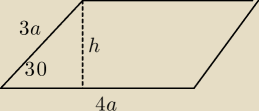
a7: zadanie 1 h/3a=sin30=1/2 czyli 3a=2h a=2/3h P=4a*h=54 4*(2/3h)*h=54 czyli h=.... czyli a=..... czyli boki 3a i 4a równają się =................

a7: to może napisz czy to zrozumiałe i jeśli nie to gdzie jest za słabo zrozumiałe

Oskar: 4*(2/3h)*h = 54 Rozumiem to, że tutaj za a wstawiliśmy 2/3h z sinusa 30 ale nie za bardzo wiem jak to rozwiązać Wychodzi mi 8/3h² =54

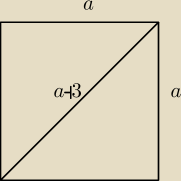
a7: zadanie 2 jaki jest wzór na przekątną kwadratu : a√2 a+3=a√2 a−a√2=−3 a(1−√2)=−3

	1+√2
a=U{−3}{1−√2*		=3(1+√2)
	1+√2

a7: 20:02 dobrze Ci wychodzi następnie h²=162/8=20,25 h=4,5

Oskar: Oooo, to zrozumiałem A zadanie z kwadratem nie można zrobić Pitagorasem? W sensie zrobiłem tak, że x² +x² = (x+3)² 2x² = x² + 9 x² = 9 x = 3 ? Bo jeżeli tak nie można to zgubiłem się przy a=U..... i nie mam pojęcia skąd to się wzięło

Bleee: Po cholerne dajesz te zadania dwa razy?

Kacper: Można, o ile dobrze stosujesz wzór skróconego mnożenia

Oskar: No dobra ale wracając do pierwszego zadania Skoro h = 4,5 to jak wyliczyć a nie znając tego odcinka przy trójkącie na 4x?

a7: a=2/3h a=3

a7: 3a=3*3=9 4a=4*3=12

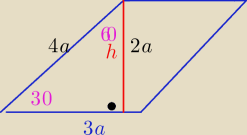
Eta: Inny sposób Zad1/ Z trójkąta "ekierki" o katach ostrych 30^o, 60^o h=2a to P=2a*3a=6a² =54 ⇒ a²=9 to a=3 boki mają długość 12 i 9 =================

Oskar: Aaa no tak. Pierwsze zadanie zrozumiałem. Dziękuję

Oskar: A o sposobie "ekierki" nigdy nie słyszałem

a7: no dobra to teraz zadanie drugie czy ekierka?

Oskar: Zadanie drugie. Nie chce sobie "mącić" w głowie sposobem którego nigdy się nie uczyłem

a7: http://www.math.us.edu.pl/prace/2001/bp/strona4.html

a7: ok zadanie drugie zrobiłeś prawie dobrze x²+x²=(x+3)² 2x²=x²+6x+9

Eta: No to ... szkoda Oskar

Eta:

Oskar: Czyli x² − 6x = 9

Oskar: Czyli nie mam pojęcia jak wyznaczyć x

a7: zad 3 https://matematykaszkolna.pl/forum/316309.html

a7: oj Oskar podpadłeś to ulubiony sposób ETY

Oskar: Nigdy mnie go nie uczono ale wydaje się być prosty i chyba pozwala zaoszczędzić dużo czasu

a7: x²−6x−9=0 Δ=36−4*(−9)=72 √Δ=6√2

a7: https://matematykaszkolna.pl/strona/54.html oblicz x

Oskar: −6 − 6√2 −−−−−−−−−−−−− 2

a7: ok i x₂ który będzie dodatni

a7: wzór jest −b czyli −(−6)=6

Oskar: −6 + 6√2 −−−−−−−−−−−−− 2

Oskar: Aaa czyli 6 − 6√2 −−−−−−−−−−−−− 2 Oraz 6 + 6√2 −−−−−−−−−−−−− 2

Oskar: x1 i x2

a7: −(−6) czyli sześć na plusie bo bierzesz do wzoru b ze zmienionym znakiem na przeciwny

a7: tak czyli 3−3√2 oraz 3+√2 pierwszy jest mniejszy od zera czyli nie może być odległością ten odrzucamy teraz liczymy pole czyli x²

a7: https://matematykaszkolna.pl/strona/55.html

a7: zadanie 6 https://matematykaszkolna.pl/strona/531.html

a7: zadanie 6

	8
k=		=2√2
	2√2

Oskar: 9+6+6√3 +3 ?

a7: (3+3√2)²=9+18√2+18=27+18√2

a7: (a+b)²=a²+2ab+b² 3²=9 2*3*3√2=18√2 3√2*3√2=9*2=18

Oskar: Nie do końca wiem skąd się wzięło to 3+ w (3+3√2)² Resztę rozumiem

a7: 20:42 tam są dwa rozwiązania 3−3√2 i drugie 3+3√2 tylko tam mi zjadło 3

a7: 3−3√2 jest mniejsze od zera odrzucamy x=3+3√2 x²=

Oskar: Aaaa i teraz wszystko jasne Czyli 18 to pole tego kwadratu

a7: pole tego kwadratu to P=27+18√2

Oskar: Chwila ale skoro x2 = 3+√2 to znaczy, że przekątna jest tyle równa? Bo jeżeli tak to wtedy bok = √2 A wtedy pole kwadratu = 2 Mylę się?

a7: zobacz jeszcze raz 20:52

Oskar: No tak czyli x2 to jest bok kwadratu tak? Nie przekątna?

a7: x oznaczyliśmy bok, x+3 przekątna

Oskar: Tak czyli 3+3√2 to przekątna mylę się?

a7: nie to jest szukany x przekątna to 6+3√2

Oskar: Bo liczyliśmy deltę z pitagorasa a pitagorasem liczyliśmy przekątną czyli x2 które jest dodatnie to przekątna? Jeżeli się mylę proszę mnie upomnieć, po prostu tak wydaje mi się logicznie

Oskar: Czyli jeżeli szukamy X to X2 wyliczony z delty to ten X? Załapałem. Dziękuję <3

a7: w Pitagorasie użyliśmy przekątnej ale był tam oznaczony x jako bok kwadratu

a7: ok

a7:

Oskar: Zrozumiałem. Już nie będę miał problemów z tego typu zadaniami, na pewno przyda się na maturze Świetnie tłumaczysz! Możemy kontynuować?

a7: to może zadanie 6

Oskar: Dobrze

a7: 20:42 teoria 20:46 rozwiązanie

a7: sorki 20:45 teoria

Oskar: Powiesz mi jak podzieliłeś/aś 8 na 2√2?

Oskar: W sensie rozumiem dlaczego tak tylko nie wiem jak Ci wyszedł taki wynik bo nie widzę tego na pierwszy rzut oka

a7: ok, to chwilką, bo robię zadanko w innym wątku i trochę mi zajmie ok?

Oskar: Okiś

Kacper: Stosunek obwodów dwóch figur podobnych jest równy skali ich podobieństwa.

Oskar: Za każdym razem? To by mi mega ułatwiło życie, bo nasza matematyczka uwielbia prawdopodobieństwo

xyz: A pola są równe skali podobieństwa do kwadratu...

Kacper: prawdopodobieństwo i podobieństwo to dwie różne sprawy

Oskar: Aaa teraz to widzę, że 2√2² to 8! Dzięki wielkie. Jesteście super

a7: nie , liczymy iloraz sumy boków , i 2√2 wyszło dlatego, że

a+b+c		a+b+c		a+b+c		1
	=		=		=
a'+b'+c'		ka+kb+kc		k*(a+b+c)		k

Oskar: Czyli nie ważne jakiego podobieństwa bym nie miał to w przypadku obwodów trójkąta skala zawsze będzie wynosić mianownik ułamka Genialne!

a7: tzn jak jeden jest trójkąt równoboczny o boku 3 a drugi równoboczny o boku 6 to skala jest 2 obwody=18/9=2

a7: zależy który trójkąt bierzemy za "wyjściowy"

a7: 9/18=1/2

Oskar: Czyli nie zawsze działa Mimo wszystko dopóki nie widzę pierwiastków dopóty podobieństwo nie sprawia mi problemów

Oskar: W Zadaniu 3 spróbowałem zastosować "ekierkę" i mam "coś" tylko nie wiem jak z tego przejść dalej

a7: no to napisz

Oskar: Staram się zrozumieć rysowanie tutaj

Oskar: No, że trójkąt jest rozwartokątny więc prowadzimy z niego wysokość więc mamy 2 boki po 45 i jeden 90 więc skoro bok = 4√2 to h=4 zgadza się?

Oskar: Czyli CB = 8? Jeżeli tak to własnie pokochałem metodę ekierki

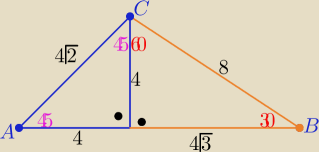
Eta: No i co? Oskar ? Sklejone dwie "ekierki" i mamy natychmiast Odp: |BC|=8 Warto się z nimi zaprzyjaźnić

Eta:

Eta: To podaj jeszcze obwód tego trójkąta

Oskar: 12 +4√2 +4√3

Oskar: I rysowałem ten trójkąt jakieś 10 minut ale zamiast "cofnij" kliknąłem "wyczyść" i no ...

Oskar: I jak tak teraz patrzę to zadanie 4 jest podobne do zadania 2giego tylko jest o wiele prostsze. Z wami czuję, że staję się coraz mądrzejszy, dziękuję

Oskar: I piąte też nagle stało się łatwe! Dziękuję za pomoc! Jeśli mogę się jakoś odwdzięczyć, śmiało to zrobię