I PKM zadanie 4
RubikSon: Wyznacz te wartości parametru s, dla których równania x2+3x+2s=0
i x2+6x+5s=0 mają po dwa różne pierwiastki, przy czym między dwoma pierwiastkami
jednego równania znajduje się dokładnie jeden pierwiastek drugiego równania
12 lut 22:03
a@b:
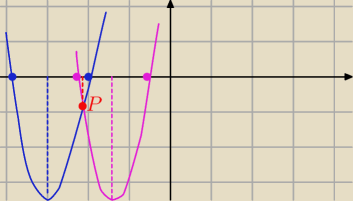f(x)=x
2+6x+5s x
w= −3 i
g(x)=x
2+3x+2s , x
w=−1,5
Warunkiem jest:
by punkt P−− wspólny obydwu wykresów musi mieć ujemny y
zatem:
x
2+3x+2s=x
2+6x+5s ⇒ x= −s i y<0
y=(−s)
2+6(−s)+5s<0
s
2−s<0
s(s−1)<0
s∊(0,1)
======
13 lut 12:58
a@b:
RubikSon
Ciężko jest z Tobą pracować! Jesteś niemową ?
Na każde zadanie : .............. ni be, ni me , ni kukuryku
13 lut 14:26
13 lut 14:27
13 lut 14:28
13 lut 14:28
13 lut 14:29
RubikSon: Halo, halo jestem. Dziękuję ślicznie za wszystkie rozwiązania. Zapłacę w mońkach
13 lut 19:20
a@b: 
13 lut 19:44
