XI PKM zadanie4
RubikSon: W trójkąt równoramienny o podstawie długości 12 cm i ramieniu długości 10 cm wpisano drugi
trójkąt równoramienny, którego końce podstawy należą do ramion trójkąta danego, a trzeci
wierzchołek jest środkiem podstawy danego trójkąta. Jakie powinny być długości boków trójkąta
wpisanego, aby jego pole było największe?
12 lut 22:11
Blee:
serio ... może jeszcze za Ciebie mamy się podpisać
12 lut 22:12
Blee:
po to je robisz żeby poćwiczyć, nieprawdaż ?!
12 lut 22:12
Tadeusz:
zacznij od rysunku
12 lut 22:14
ite: Blee w piątek etap powiatowy tego konkursu (XX edycja), więc można ćwiczyć.
12 lut 22:47
RubikSon: W sobotę xD
12 lut 23:16
ite: no tak, 15 jest w sobotę
12 lut 23:31
a@b:
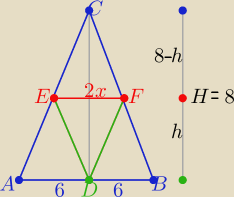
|DC|=H=8
z podobieństwa trójkątów ABC i EFC z cechy (kkk)
| 2x | | 8−h | | 4 | |
| = |
| ⇒ h=8− |
| x , x∊(0,6) |
| 12 | | 8 | | 3 | |
| | 4 | |
P(x)=− |
| x2+8x −−− osiąga maximum dla odciętej wierzchołka paraboli |
| | 3 | |
x
max=3
|EF|=2x=6
| | 6 | | 1 | |
to trójkąt DEF podobny do ΔABC w skali k= |
| = |
| |
| | 12 | | 2 | |
zatem trójkąt DEF ma wymiary : 5,5,6 i wysokości h=4
==================
12 lut 23:46
RubikSon: Dzięki
13 lut 19:21
a@b:
13 lut 19:44