mix Damian: Proponuje taki łancuszek maturalny. Kto rozwiaze wrzuca nastepne. https://matematykaszkolna.pl/forum/353268.html Zadanie 1 Dany jest wielomian W(x)=ax³−bx²−cx+d, gdzie a,b,c,d są kolejnymi liczbami naturalnymi. Wykaż, że wielomian ten ma trzy pierwiastki rzeczywiste. Oblicz, dla jakich a,b,c,d suma tych pierwiastków jest największa. Czy wielomian W(x) posiada trzy pierwiastki również w przypadku , gdy a,b,c,d są wyrazami innego rosnącego ciągu arytmetycznego o wyrazach naturalnych?

nauczyciel: Nie ucz sie , matury nie bedzie ! ! STRAJKUJEMY − nauczyciele ! ! ! Precz z maturami ! !

Damian: Co to za frustrat?

Maciess: nie wiem co z kolejnością ale robiłbym tak W(x)=ax³−bx²−cx+d a=n to b=n+1 c=n+2 d=n+3 n∊ℕ W(x)=nx³−(n+1)x²−(n+2)x+n+3 n−n−1−n−2+n+3=0 ⇒ W(1)=0 /jeden będzie pierwiastkiem Po wykonaniu schematu Hornera dla W(x) otrzymuje W(x)=(x−1)(nx²−x−(n+3)) Δ=1+4n(n+3)=4n²+12n+1 4n²+12n+1>0 dla każdego n z dziedziny, bo suma trzech składników naturalnych będzie zawsze większa od 0. Równanie będzie miało zawsze 3 pierwiastki c.n.w

	1
x1+x2+x3=		+1
	n

Nie wiem czy tu trzeba uzasadniać, ale ze znajomości funkcji homograficznej wiem ze 1/x jest w przedziale od (0,+∞) malejące więc największa wartośc sumy piewiastków będzie dla n=1 Wtedy a=1 b=2 c=3 d=4 Niech ktoś sprawdzi czy dobrze, bo nie wiem czy robić ostatnią część

ite: Pokaż jeszcze, że 1 nie jest rozwiązaniem wielomianu z drugiego nawiasu.

Maciess: załóżmy, że x=1 jest pierwiastkiem równania nx²−x−(n+3) a wtedy n−1−n−3=0 −4=0 otrzymałem sprzeczność, więc zdanie wyjściowe też jest nieprawdziwe − 1 nie jest pierwiastkiem tego równania

Maciess: druga część a₁=n>0 r>0 n,r∊N W(x)=nx³−(n+r)x²−(n+2r)x+n+3r znowu W(1)=0 W(x)=(x−1)(nx²−rx−(n+3r)) Δ=r²+4n(n+3r) znowu widać że zawsze dodatnie Sprawdzamy tę jedynkę czy nie jest piewiastkiem (znowu zakładam ze jest) n−r−n−3r=0 −4r=0 r=0 prawdziwe tylko dla ciągów naturalnych stałych (?) a dla naszych ciągów z załozenia wielomian będzie miał 3 rózne piewiastki rzeczywiste. Poprawnie?

Damian: Pierwszą częsc jest ok. Jeszcze druga.

ite: "r=0 prawdziwe tylko dla ciągów naturalnych stałych (?)" Otrzymujemy r=0, to oznacza że ciąg jest stały, więc nie spełnia postawionego w zadaniu warunku rosnącego ciągu arytmetycznego. "a dla naszych ciągów z założenia wielomian będzie miał 3 różne pierwiastki rzeczywiste" Nie zakładałeś tego, ale to wykazałeś.

Maciess: Czyli jesli lepiej by to sformułować to by było dobrze, tak?

ite: Tego zapisu nie rozumiem /15:58/ a₁=n>0 r>0 n,r∊N I jeszcze pytanie, czemu tutaj /15:16/ a=n to b=n+1 c=n+2 d=n+3 n∊ℕ nie dajesz warunku n>0?

Maciess: szybko i skrótowo (niepoprawnie). Chciałem zaznaczyć, ze to liczby naturalne. A co to 15:16 to nie wiem jak z tym 0em i jego naturalnością. Później gdy pojawiło się n w mianowniku zapmniałem dopisać, że 0 nie bedzie pasowało.

ite: 15:16 jeśli a=n to trzeba dac warunek, np. że n≠0 lub n∊N₊ żeby zagwarantować że W(x) będzie wielomianem stopnia trzeciego → żeby mógł mieć trzy pierwiastki.

Maciess: a no jasne, miałem to na uwadze jak rozwiązywałem, ale nie uwzględniłem w zapisie.

Maciess: Wstawie moze kolejne. 2. Ze zbioru liczby naturalnych siedmiocyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo wylosowania liczby podzielnej przez 4 lub przez 5, jeśli wiadomo, że jest to liczba o różnych cyfrach.

Stanislaw: https://matematykaszkolna.pl/forum/352407.html

Adamm: To może klasyka. Ile zer na końcu ma 100! ?

Ifka: Wykaż, że jeśli dwie liczby, z których jedna jest odwrotnością drugiej, są miejscami zerowymi funkcji kwadratowej f(x) = x² + bx + c, to punkt P=(0;1) należy do wykresu funkcji f

Maciess:

	1		1		1
(x−		)(x−a)=x2−ax−		x+1=x2+x(−a−		)+1
	a		a		a

punkt P to punkt przecięcia z osią OY więc c to druga współrzędna punktu P.

100!: 100! kończy się 24 −zerami

ABC: 93 326 215 443 944 152 681 699 238 856 266 700 490 715 968 264 381 621 468 592 963 895 217 599 993 229 915 608 941 463 976 156 518 286 253 697 920 827 223 758 251 185 210 916 864 000 000 000 000 000 000 000 000 istotnie

Maciess: 100!=100*99*98*...*2*1 50 liczb parzystych − 2⁵0 Liczb podzielnych przez 5 −20 Liczb podzielnych przez 25 − 4 Faktycznie 24 zera na końcu

XXX: Dla jakich wartości parametru m układ równań (2m + 3)x + (1 – m²)y = 4m² – 9 x + (1 – m)y = 4m – 10 ma dokładnie jedno rozwiązanie, które jest parą liczb o rożnych znakach?

Maciess: Obawiam sie ze gdzies rachunkowy sie wkradł bo wynik coś rozlazły. W=(1−m)(m+2) W≠0 ⇒ m≠1 m≠−2 W_x=(1−m)(6m+1) W_y=(2m+3)(2m−7)

	6m+1
x=
	m+2

	(2m−3)(2m−7)
y=
	(1−m)(m+2)

xy<0

6m+1		(2m−3)(2m−7)
	*		<0
m+2		(1−m)(m+2)

(6m+1)(2m−3)(2m−7)
	<0
(1−m)(m+2)2

(6m+1)(2m−3)(2m−7)(1−m)(m+2)²<0

	1		3		7
m∊(−∞,−2)U(−2,−		)U(1,		)U(		,+∞)
	6		2		2

Maciess: @XXX czy to poprawny wynik?

iteRacj@: policzone przez program Math24: x się zgadza

	−4m2+8m+21
y=
	m2+m−2

sprawdź jeszcze znaki, raz masz (2m+3)(2m−7) potem (2m−3)(2m−7)

uki: Z czterech kul trzy mają promień R, czwarta zaś r. Z tych kul ustawiono na stole piramidę tak, że każda z kul jest styczna do trzech pozostałych, przy czym kule jednakowe tworzą jej podstawę. a)Obliczyć największą odległość punktów kuli o promieniu r od stołu. b)Podać warunek jaki muszą spełniać promienie, aby ustawienie piramidy było możliwe.

iteRacj@: Może model przestrzenny zachęci kogoś do rozwiązania: https://www.geogebra.org/3d/wngqxssj

Eta: https://matematykaszkolna.pl/forum/88222.html Echhh ...to już 8 lat minęło?

uki: Eta ale ono nie jest rozwiazane do końca tam

Eta: Wiem,wiem Rozwiązujcie ........... powodzenia

Eta: zad 7/ Dane jest koło o środku S i średnicy AB i dwa koła o średnicach AS i BS oraz koło środku C, które ma dokładnie jeden punkt wspólny ze wszystkimi tymi kołami. Jaką część pola koła o środku S stanowi pole koła o środku C ? Powodzenia maturzyści

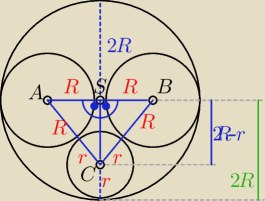
ford: Z Pitagorasa w ΔASC R² + (2R−r)² = (R+r)² R² + 4R² − 4R*r + r² = R² + 2R*r + r² 4R² − 6R*r = 0 2R(2R−3r) = 0 2R = 0 (sprzeczność) lub 2R−3r = 0

	3
R =		r
	2

P_S − pole koła o środku S P_C − pole koła o środku C P_S = π*(2R)² = π*(2*³₂r)² = π*(3r)² = π*9r² P_C = π*r²

PC		π*r2		1
	=		=
PS		π*9r2		9

uki: Obowiązuje to: Z czterech kul trzy mają promień R, czwarta zaś r. Z tych kul ustawiono na stole piramidę tak, że każda z kul jest styczna do trzech pozostałych, przy czym kule jednakowe tworzą jej podstawę. a)Obliczyć największą odległość punktów kuli o promieniu r od stołu. b)Podać warunek jaki muszą spełniać promienie, aby ustawienie piramidy było możliwe.

wredulus_pospolitus: W tym przypadku −−− tworzymy ostrosłup prawidłowy trójkąty, o krawędzi podstawy równej 2R i krawędzi bocznej r+R. Odległość środka mniejszej kuli od podłoża będzie wynosić: H_ostrosłupa + R

2		R√3
	hpodstawy =
3		3

H_ostrosłupa = √2rR + r² + 2R²/3 o ile się nie pomyliłem. To na rozluźnienie − (wiem że to zadanie kiedyś było na tym forum): Mamy dwa słupy o wysokości 50 metrów. Pomiędzy nimi został powieszony kabel o długości 80 metrów. Jaka jest odległość pomiędzy słupami, jeżeli kabel w najniższym punkcie znajduje się 10 metrów nad Ziemią?

uki: Odpowiedz Błedna

ite:

	2		2R√3
chyba		hpodstawy=		?
	3		3

uki: A mozecie to dokoczyn zanim bedzie nowe

wredulus_pospolitus:

	R√3		2		R√3
ite ... hpodstawy =		więc		h =
	2		3		3

wracając jednak do zadania: a) Obliczyć największą odległość punktów kuli o promieniu r od stołu. Mówimy więc o tym jaka będzie największa odległość dla jakiegoś konkretnego r i R punktów kuli (więc wybieramy 'górną część powierzchni kuli' więc wynikiem będzie R + r + H_ostrosłupa), czy może mam zmienne r i mamy znaleźć jaka będzie maksymalna odległość punktów kuli (biorąc po uwagę najbliżej położony stołu punkt kuli)? Wtedy (jako, ze r nie musi być mniejszy od R) rozwiązanie będzie dążyć do 2R (ale nigdy go nie osiągnie). b) musi zachodzić: (2R)² ≥ 2(r+R)² − 2(r+R)²cos60^o (promień górnej kuli nie może być na tyle mały, aby spaść 'do środka')

wredulus_pospolitus: co za głupi błąd oczywiście ... a = 2R daaaa

uki: a) brak obliczenia do końca b) mam inną odpowiedz

wredulus_pospolitus: więc jeżeli to będzie wersja pierwsza (w (a) ) to: d = R + r + √2rR + r² − R²/3 przy warunku danym w (b)

wredulus_pospolitus: ehhh b) (2R)² ≤ 2(r+R)² − 2(r+R)²cos120^o ⇔ 3(r+R)² − (2R)² ≥ 0

ite:

	2R√3
b/ R+r>
	3

uki: W końcu uff

ite: To mogę wstawić następne zadanie?

wredulus_pospolitus: Jak się ite pobawisz tym: To na rozluźnienie − (wiem że to zadanie kiedyś było na tym forum): Mamy dwa słupy o wysokości 50 metrów. Pomiędzy nimi został powieszony kabel o długości 80 metrów. Jaka jest odległość pomiędzy słupami, jeżeli kabel w najniższym punkcie znajduje się 10 metrów nad Ziemią?

ite: Znam odpowiedź, niech ktoś inny rozwiązuje.

Rita: Coś z treścią chyba nie tak, bo to musi być zawieszone pionowo

Adamm: Chyba o to właśnie chodziło.

Rita: To moze bardziej maturalne Wiemy ze f(x)=px⁴−(p+2)x², gdzie p parametr. Wyznacz wszystkie p ze fe jest roznaca w (−3;0).

Michał: Jest rosnąca tylko w tym przedziale?

Rita: tak

wredulus_pospolitus: f(x) = px⁴ − (p+2)x² lim_x−>+∞ f(x) = lim_x−>−∞ = ±∞ (w zależności od znaku parametru p) związku z tym ∃_{c ∊ Df} f↗ w (−∞,c) lub w (c,+∞)

Michał: Nie wiem czy dobrze myślę Policzyłbym pochodna i na nią nałożył warunki że musi mieć miejsca zerowe równe −3 i 0 i żeby była w tym przedziale > 0 I wyszlo mi p = −2

ite: A nie chodzi o sumę przedziałów, z których jednym jest (−3;0)?

Jerzy: @Michał, podstaw p = −2 i zobaczysz co się stanie.

Rita: Upp

iteRacj@: Ta funkcja jest parzysta dla każdej wartości parametru, nie może rosnąć jedynie w podanym przedziale.

Rita: Chodzi o to aby była rosnąca w nim, a może jeszcze rosnąc sobie gdzie indziej tez

iteRacj@: O 14:35 było powiedziane, że tylko w nim.

Jerzy : Funkcja musi osiągać tylko dwa ekstrema lokalne: f(−3) minimum i f(0) maksimum.

iteRacj@: @Jerzy Skoro to f.parzysta, to jeśli będzie miała te dwa ekstrema, to wtedy jeszcze będzie trzecie dla f(3) ?

Rita: Jakos zle zrozumiałam o 14:35 bo tam bład poełniłam przy wyrazie rosnaca

uki: odswiezam

Jerzy: @iteRacj@ , słuszna uwaga, ten fakt mi umknął.

ite: @uki Jeśli jesteś maturzystą, to spróbuj rozwiązać to zadanie. Zacznij od obliczenia pochodnej, potem ekstrema zgodnie z 21:11.

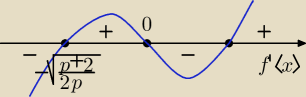
iteRacj@: f(x) = px⁴−(p+2)x² f'(x) = 4px³−2(p+2)x=2x[2px²−(p+2)] 1/ p=0 2*0*x²−(0+2)=0 ← sprzeczność

	p+2
2/ p≠0 x2−		=0 → [x−√(p+2)/(2p) ]*[x+√(p+2)/(2p) ]=0
	2p

x=0 lub x=√(p+2)/(2p) lub x=−√(p+2)/(2p) f(x) ma osiągać ekstrema lokalne: dla x=−3 minimum i dla x=0 maksimum sprawdzam, kiedy pochodna przyjmuje wartość 0 i w jaki sposób zmienia znak dla x∊( −∞;−√(p+2)/(2p) ) f'(x)<0 więc f(x)↘ dla x∊( −√(p+2)/(2p);0 ) f'(x)>0 więc f(x)↗

	2
stąd −√(p+2)/(2p)=−3 p=
	17

	2
Dla p=		podana funkcja jest rosnąca w przedziale (−3;0).
	17

iteRacj@: Dodaję następne zadanie maturalne (z profilu podstawowego). Rozwiąż równianie

	2		4
1+		+		+...=k
	x		x2

gdzie k jest rozwiązaniem równania log₂(k+3)+log₂8=4+log₂(k−1)

	5
Odp. k=5, x=
	2

Maciess: log₂(8k+24)=log₂16+log₂(k−1) log₂(8k+24)=log₂(16k−16) / log₂ jest funkcją różnowartościową więc mozemy porównać argumenty funkcji 8k+24=16k−16 −8k=−40 k=5

	2
q=		x≠0
	x

	1
S=
	1−2/x

1
	=5
1−2/x

	10
1=5−		/*x
	x

x=5x−10

	5
x=
	2

Tu musiałbym pokazać jeszcze, że |q|<1 ?

iteRacj@: Zacznij od założenia |q|<1. Wtedy możesz zastosować wzór na sumę wyrazów. I masz pewność, że nie dzielisz przez 0.