... peja: Z czterech kul trzy mają promień R, czwarta zaś r. Z tych kul ustawiono na stole piramidę tak, że każda z kul jest styczna do trzech pozostałych, przy czym kule jednakowe tworzą jej podstawę. Obliczyć największą odległość punktów kuli o promieniu r od stołu.

peja: up

peja: up

peja: up

peja: up

peja: up

peja: up

peja: up

peja: up

peja: up

cv: masz jakąś odpowiedź do tego

peja: nie

peja: pomożesz?

kamis: Może coś takiego: Jeśli połączysz środki tych kuli powstanie ostrosłup prawidłowy trójkątny Długość krawędzi podstawy − 2R, R > 0 Długość krawędzi bocznej − R + r, r > 0

	2R√3
Wysokość podstawy −		= R√3
	2

	2		2R√3
Odcinek łączący wierzchołki podstawy z ortocentrum −		* R√3 =
	3		3

	2R√3
Długość wysokości ostrosłupa: h = √(r + R)2 − (		)2 i h > 0 ⇔ (r + R)2 >
	3

	2R√3
(		)2
	3

	2R√3
Największa odległość: r + √(r + R)2 − (		)2 + R
	3

peja: dziękuję

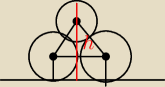
.: h= R+r+r²+2Rr

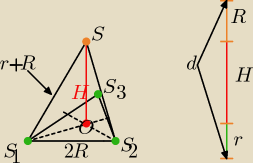
Eta: środki kul małych tworzą trójkąt równoboczny o boku dł. "2R" Wszystkie cztery środki są wierzchołkami ostrosłupaS₁S₂S₃S Spodek wysokości tego ostrosłupa pokrywa się ze środkiem O w podstawie Krawędzie boczne tego ostrosłupa maja długość : R+r z tw. Pitagorasa wyznacz dł. H

	2		2R√3
IS1O|=		*		=........
	3		2

szukana odległość d= R+H+r Sorry za koślawy rysunek

Eta: Ooo .... widzę,ze już cała gromada pomocników była przede mną

peja: dziękuję pięknie wszystkim mam jeszcze pytanie czy istnieje jakaś suma dla

	1		1		1		1
an=		+		+		+...+
	1		2		3		n

bo nie wiem jak sprawdzić czy któryś wyraz jest większy od 2009