dowod kristoff: uzasadnij ze dla każdego x≥2/3 prawdziwa jest nierówność x2−x3≤1/6

Eta: https://matematykaszkolna.pl/forum/344202.html

Eta: https://matematykaszkolna.pl/forum/374142.html

Eta: https://matematykaszkolna.pl/forum/371938.html

Mila:

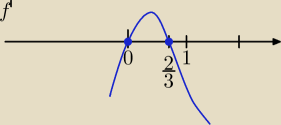
	1		2
f(x)=x2−x3−		i f(x)≤0 dla x≥
	6		3

f'(x)=2x−3x² Ekstrema : 2x−3x²≥0 x*(2−3x)≥0

	2
x=0, x=
	3

	2
f'(x)>0 dla x∊(0,		)
	3

	2
x=0 − min lokalne , x=		maksimum lokalne
	3

	2		2		2		1		4		8		1		4		1
fmax=f(		)=(		)2−(		)3−		=		−		−		=		−		=
	3		3		3		6		9		27		6		27		6

	1
=−
	54

	2
dla x≥		funkcja f(x) jest malejąca⇔
	3

	2
f(x)≤0 dla x≥
	3

Mila: Niepotrzebnie pisałam

kristoff: dziekuje

PW: Sposób bez badania funkcji. Badana nierówność ma równoważną postać

	1		2
x3+		≥x2 dla x≥		.
	6		3

Nierówność między średnią arytmetyczną a geometryczną daje dla dodatnich x

	x3		x3		1
		+		+		≥33√x6/24=3x2 3√1/24>3x2 3√1/27=x2,
	2		2		6

co kończy dowód.

	2
Jak widać, w dowodzie nie korzystaliśmy z założenia x≥		, wystarczyło x>0.
	3

	1
To samo widać w dowodzie Mili − badana funkcja na (0,∞) ma maksimum równe −		, a
	54

więc dla wszystkich dodatnich x przyjmuje wartości ujemne.

wiktor: Oceń prawdziwość poniższych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, lub F — jeśli jest fałszywe. Przekątne prostokąta mogą mieć długości 3cm i 4cm. P F Można skonstruować trójkąt, którego boki mają długości: 3cm, 4 cm i 5cm. P F Wszystkie kąty trójkąta prostokątnego są proste. P F prosze o pomoc

wiktor: mam problem prosze o pomoc Jedna paczka waży 6 kg 5 dag, a druga waży 4,8 kg. O ile kilogramów druga paczka jest lżejsza od pierwszej paczki?

PW: A gdzie się wpisałeś, wiktorze, pod zadaniem z analizy? Nikt nie wpadnie na pomysł, że pod tematem "uzasadnij prawdziwość nierówności" kryje się zadanie z geometrii.

wiktor: bo ja niewiem gdzie to pisa trzeba