monotoniczność funkcji Szczeniak:

	2		1
Uzasadnij, że dla każdego x≥		prawdziwa jest nierówność x2−x3≤
	3		6

La gringa: f(x) = x² − x³

	1
g(x) =
	6

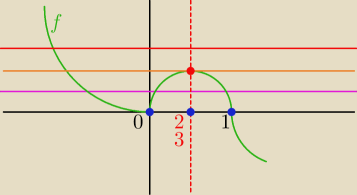
zał. x∊(2/3;∞) x²−x³=0 x²(1−x)=0 x₁=0 − pierwiastek podwójny x₂=1 − pierwiastek pojedyńczy Rysujemy wykres f(x) metodą wielomianową i prostą g(x). Widzimy że w przedziale (0,∞) funkcja f(x) ma gdzieś swoje ekstremum maksimum. Musimy stwierdzić jak będzie wyglądał wykres w tym przedziale (czy będzie styczny, przecinał prostą, leżał pod prostą) Liczymy ekstremum. f'(x) = 2x − 3x² Warunek konieczny istnienia ekstremum: f'(x) = 0 ⇒ x(−3x+2)=0 x₁ = 0 − nie spełnia założeń.

	2
x2 =
	3

Warunek konieczny zmiana znaku pochodnej w otoczeniu miejsca zerowego. Rysujemy wykres licznika pochodnej. Widzimy że w otoczeniu x₂ zmienia ona znak z + na − Czyli dla x=2/3 osiąga ona swoje maksimum. Wiemy że jest to największa wartość w przedziale (0;∞) Musimy teraz tylko określić wartość tego argumentu dla f(x) dzięki temu dowiemy się jak wygląda ten wykres względem prostej g(x)=1/6.

	22		23		4
f(2/3)=		−		=		. To jest maksimum w przedziale (0;∞)
	32		33		27

4:27 ≈ 0,148 1:6 ≈ 0.166 Wniosek: wierzchołek leży poniżej prostej g(x). [c[(nasze g(x) będzie zatem funkcją czerwoną)]

	2
Ponieważ interesuje nas przedział x∊<		; ∞) a wierzchołek f(x) osiąga swoje maksimum
	3

	2		2
właśnie w		i jest ono mniejsze niż wartość funkcji g(x) w
	3		3

	2
To otrzymujemy f(x)≤g(x) dla x∊(		,∞) co należało dowieść.
	3