monotoniczność funkcji, help pepepe: 1. Wyznacz przedziały monotoniczności funkcji f(x)= 1+(x²−3x+1) +(x² −3x +1)² + ... jeżeli wyrażenie to jest sumą szeregu geometrycznego zbieżnego. 2. Uzasadnij, że dla każdego x≥ ²₃ prawdziwa jest nierówność x² − x³ ≤ ¹₆

heheszek: 1. skoro jest zbiezny, to przedzial dla ktorego jest zbiezny: |x²−3x+1| < 1 jak juz to wyznaczycz to

	a1		1
S =		=
	1−q		1−(x2−3x+1)

potem policz pochodna z tego i gdy S' > 0 to funkcja rosnie gdy S' < 0 funkcja maleje S' = 0 jest stala przy kazdym z przedzialow nalezy sprawdzic zgodnosc z dziedzina ta z 1.

Basia: ad.1 aby szereg był zbieżny musi być |q|<1 q = x²−3x+1 |x²−3x+1}<1

⎧	x2−3x+1<1
⎨	i
⎩	x2−3x+1>−1

⎧	x2−3x<0
⎨	i
⎩	x2−3x+2>0

⎧	x(x−3)<0
⎨	i
⎩	(x−1)(x−2)>0

⎧	x∊(0;3)
⎨	i
⎩	x∊(−∞;1)∪(2;+∞)

x∊(0;1)∪(2;3) wtedy (i tylko wtedy)

	1		1		1
f(x) = S =		=		=
	1−(x2−3x+1)		−x2+3x		−x(x−3)

dla x∊(0;1)∪(2;3) funkcja y= −x(x−3) przyjmuje wartości dodatnie dla x∊(0,1) y= −x(x−3) jest rosnąca dka x∊(2;3) y= −x(x+3) jest malejąca stąd:

	1
f(x) =		jest malejąca w przedziale (0,1); a rosnąca w przedziale (2;3)
	−x(x+3)

no chyba, że koniecznie chcesz liczyć pochodną

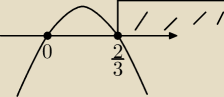
heheszek: 2.

	1
Uzasadnic ze x2 − x3 −		≤ 0
	6

Niech f(x) = x² − x³ − 1/6 f'(x) = 2x − 3x² 2x − 3x² = 0 x(2−3x) = 0

	2
x = 0 lub x =
	3

	2
uwzgledniajac x ≥
	3

mamy

	2
f'(x) < 0 dla x ≥		i wtedy funkcja maleje
	3

	2
skoro maleje to pytanie jaka ma wartosc w punkcie
	3

	2		2		2		1		4		8		1
f(		) = (		)2 − (		)3 −		=		−		−		=
	3		3		3		6		9		27		6

	24		16		9
=		−		−		< 0
	54		54		54

	2
zatem mamy ze funkcja w punkcie x =		ma wartosc ujemna
	3

oraz ze jest malejaca od punktu c.k.d