Problem z rozwiązaniami zadań polo: Proszę o pomoc z tymi zadankami:

	a2−1		b2−1
1) https://matematykaszkolna.pl/forum/365081.html Nie mam zielonego pojęcia skąd wzięło się równaie		=
	a		b

2) https://matematykaszkolna.pl/forum/371419.html Tutaj nie mam pojęcia skąd wzięły się te 4 równania 1) b = a*q⁴ 2) a1(1+q) = 4 3) a1(1+q)*q² = 36 −> q² = 9 −> q = +/− 3 4) czyli b = 81a

	α   a*sin   2
3) https://matematykaszkolna.pl/forum/371418.html Tutaj problem z pojęciem skąd wzięło się równanie R=
	sinα

Wyjaśniłby ktoś skąd się to wzięło? Byłbym bardzo wdzięczny

PW: 1) Zrób sobie ilustrację, to pomoże zrozumieć, że rozwiązujący korzysta z podobieństwa trójkątów (inaczej mówiąc wyznacza na dwa sposoby tangens kąta nachylenia prostej przechodzącej przez C).

polo: @PW Dzięki za pomoc w tym zadanku, ale jeszcze mam pytanie do samej równości. Czemu wynika z niej, że ab=−1?

PW: Cóż, rozwiązujący jest mistrzem i pewne rzeczy są dla niego oczywiste. W tym wypadku trzeba dokonać przekształcenia

	a2−1		b2−1
		=
	a		b

	1		1
a−		=b−
	a		b

	1		1
a−b=		−
	a		b

	b−a
a−b=
	ab

a−b nie jest zerem, a więc ab=−1 Oczywiście jest to łatwe, ale mało kto wpadnie na to, że taki wniosek za chwilę można wykorzystać

polo: @PW Jeszcze raz wielkie dzięki A można jeszcze jakieś rady odnośnie dwóch pozostałych pytań?

polo: bump ktoś jeszcze pomoże?

iteRacj@: zadanie 2/ x₁ + x₂ = 4 x₃ + x₄ = 36 a = x₁*x₂ b = x₃*x₄ 1) dlaczego b = a*q⁴ ? b = x₃*x₄=x₁*q²*x₂*q²=x₁*x₂*q⁴=a*q⁴ 2) a₁(1+q) = 4? a₁=a=x₁ x₁ + x₂ = 4 a + a*q = 4 a(1 +q) = 4 3) a₁(1+q)*q² = 36 ? a₁(1 +q) =x₁ + x₂ = 4 a₁(1+q)*q² =(x₁ + x₂)*q²=x₃ + x₄ = 36 a czwarte to wyliczenie z poprzednich

polo: @iteRacj@ Serdeczne dzięki Ktoś ma jeszcze pomysły co do zadanka ostatniego?

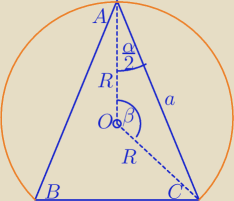
iteRacj@: R − promień okręgu opisanego na podstawie ostrosłupa β=180^o−α/2−α/2=180^o−α z tw.sinusów dla ΔAOC

a		R
	=
sin(180o−α)		sin α/2

a		R
	=
sin α		sin α/2

a		R
	=
sin α		sin α/2

	a*sin α/2
stąd R=
	sin α

może === jako autor dać znać, czy akurat w ten sposób było liczone ?