geometria analityczna mk: W trójkącie prostokątnym ABC (|<ABC|=90stopni) dwa wierzchołki mają współrzędne A(4,−5) i C(−8,5). Wyznacz współrzędne wierzchołka B, wiedząc, że pole ΔABC jest równe 61. Pomoże ktoś? Jakoś nie mam pomysłu na to zadanie

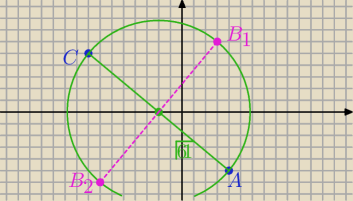
Qulka: 2√61•h/2 = 61 więc h=√61 więc h= R B1(3;6) lub B2 (−7;−6)

mk: Ok, ale jak dalej obliczasz B?

Qulka: prostopadła do AC przechodząca przez środek

mk: Tylko skąd wiadomo, że AC przechodzi przez środek?

Qulka: https://matematykaszkolna.pl/strona/1223.html https://matematykaszkolna.pl/strona/1750.html https://matematykaszkolna.pl/strona/42.html https://matematykaszkolna.pl/strona/1468.html i układ równań z okręgu i tej prostej daje punkty B1 i B2

Qulka: bo wysokość musi być równa R bo z pola tak wynika

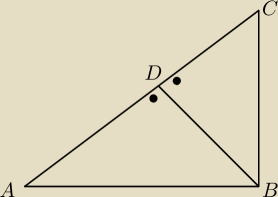
Basia: AC jest przeciwprostokątną |AC| = √(−8−4)²+(5+5)² = √144+100 = √244 = √4*61 = 2√61 BD −wysokość poprowadzona z wierzchołka B

	1
P=		*|AC|*|BD| = 61
	2

|AC|*|BD| = 2*61 2√61*|BD| = 2*61 |BD| = √61

	|AC|
ale promień okregu opisanego na tym trójkącie R=		= √61
	2

z tego wynika, że D jest środkiem odcinka AC D(−2;0) BD^→⊥AC^→ BD^→ [−2−x; 0−y] AC^→=[−12;10] −12(−2−x)+10*(−y) = 0 24+12x−10y = 0 12x−10y+24=0 10y = 12x+24 5y = 6x+12

	6x+12
y =
	5

(−2−x)²+(−y)² = 61 4+4x+x²+y²=61

	36x2+144x+144
4+4x+x2+		= 61 /*25
	25

100+100X+25X²+36X²+144X+144=61*25 61X²+244X+244 = 61*25 /:61 x²+4x+4=25 x²+4x−21=0 dokończysz?

mk: Ok, dziękuje wam bardzo