W prostokątnym układzie współrzędnych zaznacz zbiory A, B, A∩B Adek: W prostokątnym układzie współrzędnych zaznacz zbiory A, B, A∩B Nie rozumiem trygonometrii stąd problem u mnie w tym zadaniu, proszę o pomoc z wyjaśnieniem zwłaszcza zbiorów z użyciem trygonometrii. a) A={(x,y): xy≤0} B={(x,y): ctg (x+y)=1} b) A={(x,y): cos (x+y)=0} B={(x,y): tg y=1

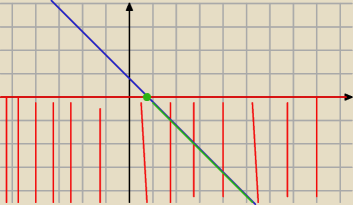
5-latek: a) A xy≤0 to y≤0 zbior zaznaczony na czerwono wraz z osia OX B) tutaj musi ktos sprawdzuc ctg(x+y)=1

	π
ctg(x+y)= ctg
	4

	π
x+y=
	4

	π
y=		−x niebieska linia
	4

Tutaj π traktuje jako liczbe a nie kat Ktos musi sprawdzic B dlatego ze nie jestem pewnien czy nie trzeba bedzie rysowac

	π
y=−x+		+kπ
	4

gdzie k∊C

5-latek: Chcialbym wiedziec dla siebie czy dobrze .

Pytający: Oj źle, 5−latku. a) A={(x,y): xy≤0} Podana nierówność zachodzi, gdy x i y mają różne znaki lub, gdy którekolwiek jest równe 0, czyli wykresem będzie: druga ćwiartka + czwarta ćwiartka + osie. https://www.wolframalpha.com/input/?i=plot+xy%3C%3D0 B={(x,y): ctg (x+y)=1} ctg (x+y)=1

	π
x+y=		+kπ // patrz: 429
	4

	π
y=−x+		+kπ dla k całkowitego, tu masz wykres (każda prosta odpowiada jakiemuś
	4

współczynnikowi k): https://www.wolframalpha.com/input/?i=plot+ctg(x%2By)%3D1 Część wspólna to tamte proste bez ich fragmentów w ćwiartkach pierwszej i trzeciej. b) A={(x,y): cos (x+y)=0} cos (x+y)=0

	π
x+y=		+2kπ // patrz: 427
	2

	π
y=−x+		+2kπ dla k całkowitego
	2

https://www.wolframalpha.com/input/?i=plot+(cos(x%2By)%3D0) B={(x,y): tg y=1}

	π
y=		+kπ, dla k całkowitego // patrz: 428
	4

Tu wykresem są proste poziome (znowuż każda prosta odpowiada jakiemuś współczynnikowi k) Część wspólna to punkty przecięć wykresów: https://www.wolframalpha.com/input/?i=plot+(tg(y)%3D1+and+cos(x%2By)%3D0)

5-latek: dziekuje CI