Stereometria danek: Dany jest sześcian ABCDA'B'C'D'. P jest punktem przecięcia się przekątnych ściany bocznej

	a√6
AA'DD'. Wykaż, że odległość punktu P od przekątnej BD' sześcianu jest równa
	6

Proszę o pilną pomoc...

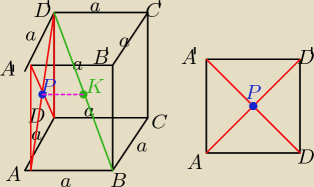
danek: Jak to powinno być?

	a√6
|PK| =
	6

ale ta odległość może być w dowolnym punkcie czy na środku tej przekątnej?

danek: kto jest w tym dobry... spojrzy ktoś na to?

danek: czy jest może paziówna lub Bogdan na forum? może wy byście umieli pomóc?

benek: hmm trzeba to zrobic

danek: mam kilka zadań i męczę się tak z nimi...

danek: i co myślisz na tym benek?

benek: nie wiem co myslesc sprawdz jeszcze tresc tego zadania. bo mi nie wychodzi,, trzeba znalezc haczyk

danek: powinno się wyznaczyć najpierw przekątną sześcianu, tylko jak?

danek: treść przepisałem dobrze...

danek: do zadania mam jeszcze punktacje: 1p Wyznaczenie długości przekątnej sześcianu: |BD'| = a√3

	x		a
1p Zapisanie równania wynikającego z treści zadania:		=
	√2   a   2		a√3

	a√6
1p Rozwiązanie równania: x=
	6

ale ja potrebuje po kolei jak to rozwiązać...

danek: https://matematykaszkolna.pl/forum/33406.html https://matematykaszkolna.pl/forum/33410.html https://matematykaszkolna.pl/forum/33412.html oprócz tego mam jeszcze 3 zadanka... może te są łatwiejsze... spojrzysz?

Marek: Pomozesz mi w zadaniu? dziedzina funkcji f jest przedzial <1;5> a jej zbiorem wartosci przedział <−2;6> wykres funkcji g powstal przez przesuniecie wykresu funkcji f o wektor podaj dziedzine funkcji i zbior wartosci funkcji g. B) u= (3,0) Dg= g(Dg)= C) u=(2,5) Dg= g(Dg)= D) u=(−1,−3) Dg= g(Dg)=

benek: dobra to robimy

Marek: Oooo wielkie dzieki nie moge tego zrozumiec

benek: kurde ale syf, napisalem juz a tu lipa zepsulo sie

Marek: kurde

danek: do Marka: B) Dg= <4;8> ZWg= <−2;6> C) Dg= <3;7> ZWg= <3;11> D) Dg= <0;4> ZWg= <−5;3>

Marek: do danek a mogl bys pokazac mi jeden przyklad na wykresie bede wdzieczny?

Marek: dzieki za pomoc

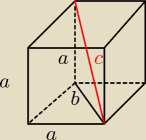
benek: b²=a²+a² b²=2a² b=a{2} c²=a²+b² c²=a²+(a{2})² c²=a²+2a² c²=3a² c=a{3} to jest pierwszy punkt

benek: a{2}=a√2 a{3}= a√3

benek: teraz z twierdzenia talesa wiemy ze: PK do AP ma się tak samo jak AB do BD' PK=x AP=a√2/2 AB=a BD'=a√3

danek:

danek: to jest dla marka i tutaj poprostu przesuwasz wektorrem

Marek: oooo dzieki juz rozumiem

danek: czyli teraz to tylko proporcja, tak benek?

benek:

x
	=aa√3
a√22

więc xa√3=^a2√2₂ x=^a2√2_2a√3 x=^a√2_2√3 teraz pozbywamy sie niewymiernosci z mianownika x=^a√2*√3_2√3*√3= ^a√6₆

danek: no faktycznie teraz się wszystko zgadza a benek spojrzał byś jeszcze na moje 3 inne zadanka? wyżej miałem do nich linki

benek: gotowe

benek: zaraz spraqdze

Marek: Naszkicuj wykers funkcji f. Pozesz jeszcze w tym jednym zadaniu ? a) f(x)= −Ix+2I b) f(x)= −Ix−1I c) f(x)= 2 −Ix−4I d) f(x)=3 −Ix+2I e) f(x)= −(x+1)² f) f(x)= 1−(x−4)²