Kangur - gdzie znajdę?
Jack: Szukam przykładowych zadań z kangura...klasa 3 LO.
Ktoś by mógł podrzucić linka, albo jakieś zadanka?
21 gru 16:02
21 gru 17:08
Jack: yyy? xd
chcialem tylko do konkursu potrenowac...
21 gru 17:23
Eta:
1/
W trapezie przekątne maja długości 15 i 20 , zaś wysokość ma długość 12
Wyznacz pole tego trapezu
Powodzenia

21 gru 17:39
Metis: Eta z podobieństwa trójkątów?
21 gru 17:50
kyrtap:
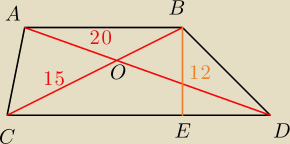
Eta dobrze idzie mi jak narazie?

21 gru 18:03
Jack: Pole = 150...
21 gru 18:04
Eta:
Mało P=150 lub P= 42
21 gru 18:08
Jack: hmm... czyli co...odwrocony trapez drugi przypadek? :x
21 gru 18:09
Eta:
Myślenie nad drugim przypadkiem ........ zostawiam Tobie

21 gru 18:10
Jack: jakżeby inaczej ^^
21 gru 18:11
Jack:
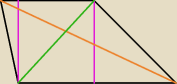
Rozumiem ze to oto chodzi...o ile to mozna nazwac trapezem, ale zapewne tak skoro ma jedna pare
bokow rownoleglych
21 gru 18:16
Eta:

21 gru 18:21
Jack: hmm...ten przypadek juz nie jest taki banalny...
21 gru 18:21
Jack: co tu sie stalo : D
21 gru 18:22
Jack: to moj rysunek nie pasuje?

Jaka jest definicja trapezu ? ; o
21 gru 18:23
Jack: ok, dobra, z twojego da sie chociaz to wyliczyc...
| | (x + 7−x)12 | |
P = |
| = 6 * 7 = 42 |
| | 2 | |
21 gru 18:30
Qulka: Twój rysunek też pasuje ale wychodzi w nim pole =150
21 gru 18:42
Eta:

21 gru 18:47
Jack: @Eto, jak zrobic zad 3 z tego linku co wyslalas ? : D...bo kurcze, licze jakos na okolo,
na pewno nie potrzebnie
21 gru 18:48
Eta:
Odp: C)
21 gru 18:51
Jack: a dlaczego akurat tak? : D
21 gru 18:52
Eta:
α∊IV ćw sinα<0 cosα >0 i tgα<0
| | √2 | |
tgα = − |
| = tg(180o−α) ∊ II ćw |
| | 4 | |
21 gru 19:02
Jack: yyy...to czemu ten Cosinus nie pasuje? ; o
21 gru 19:08
Jack: a... dobra
chodzi o to ze
cos (90 ± α ) = ±sin α
21 gru 19:09
Jack: to jednak nie rozumiem xd
21 gru 19:14
Jack: wynik zad 6 ? ; x
21 gru 19:34
21 gru 19:55
Eta:
6/ z tw. kosinusów c
2=....
c= 2
√37≈ ...... i koduj

21 gru 19:58
Eta:
c= √148= 12,165525060 ........
21 gru 19:59
Jack: no wlasnie tak mi wyszlo, tylko z drugiej strony jak spojrzalem...
to to moze byc 6,8,10 ; D...trojkat prostokatny, chocaiz nie moze bo tam jest kat 120
stopni...ale jakby nie bylo
21 gru 20:02
Jack: zadanie 16...
to nie jest po prostu
(−1) * 2 = −2?
21 gru 20:03
Eta:
R(x)= −x
21 gru 20:22
Jack: xd?
21 gru 20:47
olekturbo: Eta,
mogłabyś zrobić zadanie z dowodzeniem z trapezem z tej maturki co wysłałaś? Z resztą daję sobie
radę

21 gru 21:17
Eta:
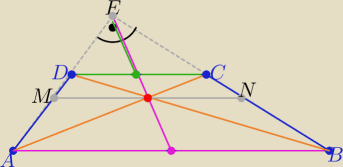
Wskazówka na rys ( powinien wystarczyć
Dodaj teraz odpowiednie komentarze
21 gru 21:36
Jack: jakie dowodzenie z trapezem? : O
21 gru 21:57
Eta:
zad 10/

21 gru 21:59
22 gru 00:22
olekturbo: 
22 gru 00:45
Eta:
Olek ....co masz taką smutną minkę ?

22 gru 00:47
22 gru 00:50
Eta:

22 gru 21:16
Jack: 
Robię zad 11 z tego linku (Post: 00;22)
22 gru 21:17
Jack: i pytanko...czy zad 9.
wynik −1 ?
22 gru 21:19
Eta:
Już wykazałeś ? ( wystarczy 2 min i gotowe

22 gru 21:21
Eta:
zad 9/ (−1) ?

22 gru 21:24
22 gru 21:28
Jack: Ale wynik ok?
22 gru 21:30
Eta:
Teraz ok

22 gru 21:30
Jack: w zadaniu 10 wyszlo mi, ze
x= 354
Znowu pomylilem posty...lepiej zamkne tamta karte...
22 gru 21:31
Eta:
Piłeś coś?

22 gru 21:32
Jack: To moge przedstawic tok rozumowania : D
24311 − 8114 + 7x = 927
(35)11 − (34)11 + 7x = (32)27
355 − 356 + 7x = 354
7x = 354 − 355 + 356
7x = 354(1−31 + 32)
7x = 7 *354
x = 354
22 gru 21:33
Eta:
ok

22 gru 21:39
Jack: Jesli mam polecenie : Oblicz obwod trojkata
znam bok i 2 kąty...moge tw. sinusów? czy musze cosinusów...
bo z kątami zawsze lepiej cosinusów bo sinus ma wartosci dodatnie w 0;180 i dlatego najczesciej
sa 2 mozliwosci : D
22 gru 21:47
Eta:
Tw kosinusów gdy mamy dane:
1/ trzy boki
2/ dwa boki i kąt zawarty między nimi
w pozostałych przypadkach ... tw. sinusów
22 gru 21:57
5-latek: Zadanie :
=========
Nauczyciel polecil trzem uczniom wykonać mnożenie dwóch liczb
Jeden z nich dodając iloczyny czastkowe zgubil jednostke ktoregos rzedu dziesiętnego a
sprawdzając wykonanie działania za pomocą dzielenia uzyskanego przez mnożnik , otrzymal iloraz
971 i reszte 214.
Drugi uczen zgubil w dodawaniu 2 jednostki następnego wyzszsego rzedu i przy sprawdzaniu tym
samym sposobem co pierwszy otrzymal iloraz 965 i reszte 198.
Trzeci uczen zgubil jednostke dalszsego jeszcze wyzszsego rzedu i przy sparwdzaniu miał iloraz
940 i reszte 48.
Znalezc dane do mnożenia lczby i wskazać w których miejscach uczniowie popełnili bląd .
Pewnie będzie łatwe dla Ciebie

22 gru 21:59
Jack:
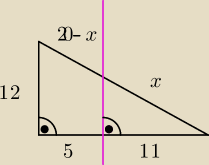
Czy moge ulozyc proporcje
22 gru 21:59
Eta:
Zmierz się z takim zadaniem:
W trójkącie ABC w którym |AB|=6, |BC|=8
dwusieczna kąta ABC przecina bok AC w punkcie M tak,że |BM|=|AM|
Oblicz długość boku |AC|.
Podaj najprostsze rozwiązanie

22 gru 22:01
Jack: Nie dam rady Eto
Nie znam własności dwusiecznej : D oprócz tego, że dzieli kąt na pół
22 gru 22:03
Eta:
do wpisu
21: 59
tak

22 gru 22:03
Eta:
A w której klasie jesteś?
22 gru 22:04
Jack: maturalna... ; /
ale jak zawsze braki wiedzy elementarnej...
tak samo nie wiem co to iloczyn czastkowy ani mnoznik ; d
22 gru 22:05
Eta:
I to ,że dwusieczna dzieli kąt na pół wystarczy do rozwiązania tego zadania !
22 gru 22:05
Jack:
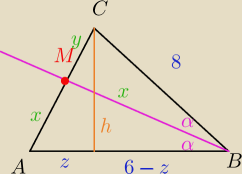
Przed chwila "obczailem", ze jak mamy dwusieczna
to mamy taka rownosc...
6 y = 8 x
z
2 = (x+y)
2 − h
2
h
2 = 64 − (6−z)
2 = 64 − (36 − 12z + z
2) = − z
2 + 12z + 28
oraz
| | 4x | | 7 | | 49 | |
h2 = (x+ |
| )2 − z2 = ( |
| x)2 − z2 = |
| x2 − z2 |
| | 3 | | 3 | | 9 | |
Porównujemy h...
| | 49 | |
− z2 + 12z + 28 = |
| x2 − z2 |
| | 9 | |
108z + 252 = 49x
2
.
.
.
czekaj bo sie zgubilem xd
22 gru 22:32
Jack:
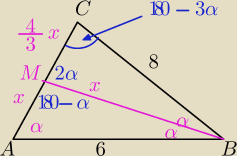
ewentualnie kątami...
22 gru 22:41
Jack: tam powinno byc zamiast
180 − α : 180 − 2α, aczkolwiek i tak obydwoma sposobami na okolo licze ; d
22 gru 22:57
Eta:
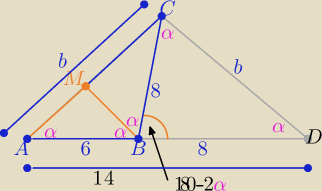
ΔADC równoramienny i ΔDBC −− równoramienny i podobne z cechy (kkk)
to:
22 gru 23:23
Eta:
Poprawiam chochlika

22 gru 23:26
Jack: skad wgl ten stosunek...
b/14 = 8/b
hmm
a dlaczego nie np.
b/6 = 8/b
23 gru 00:17
Eta:
ΔADC ( duży) ∼ ΔDBC (małego po prawej)
| | |AC| | | |BD| | | b | | 8 | |
to: |
| = |
| ⇔ |
| = |
| |
| | |AD| | | |CD| | | 14 | | b | |
23 gru 00:56
Kacper:

23 gru 10:28
Jack: Dobra, dzieki...
i tak tego nigdy nie zrozumiem ; D
23 gru 14:06
Kacper:
Nigdy nie mów nigdy

23 gru 14:07
Jack: hehe
23 gru 14:18
5-latek: rozwiąż równanie
√xlog√x=10
23 gru 18:46
5-latek: I jeszcze jedno
Dowiesc ze jeżeli
a
12+b
12+c
12=1
a
22+b
22+c
22=1
to
−1≤a
1a
2+b
1b
2+c
1c
2≤1
Na razie wystarczy Ci

23 gru 18:52
Kacper:
Ja już

23 gru 18:52
zombi: Bo matematyki się nie rozumie, tylko się do niej przyzwyczaja. Jak to powiedział bodjaże John
von Neumann
23 gru 18:52
5-latek: I może jeszcze takie dla zabawy
Dowiesc opierając się na rownosci
23 gru 19:07
5-latek: Czesc
Kacper 
23 gru 19:08
Kacper:
zombi ciekawe stwierdzenie.
5−latek nie masz czasem gadu? mam pewna kwestię do obgadania.
23 gru 19:13
5-latek: Nie mam Kacper .
Napisz na emala .
23 gru 19:21
Kacper:
Napisałem.
23 gru 19:24
Jack: zombi zazwyczaj matematyke rozumiem, a niektore rzeczy biore na "tak musi byc", i wlasnie
takie porownywanie dlugosci w trojkacie to "tak musi byc"
23 gru 20:01
Eta:

23 gru 20:08
Jack: √xlog √x = 10 // ()2
xlogx ^^√x = 100
log10 xlog/sup>1/sup>0 p{x} = 100
hmmm
chwilke ... xd
23 gru 20:23
5-latek: x>0 i u=√x
dostaniesz równanie
ulogu=10 rozwiązuj dalej
23 gru 20:28
Jack: jesli u = √x
to powinno byc
u2logu=10
23 gru 20:29
Jack: czy istnieja wzory na mnozenie logarytmow? ; o
23 gru 20:35
5-latek: No niestety nie istnieja
23 gru 20:36
Jack: Zaczynam od obustronnie do kwadratu...
nastepnie mnoze razy logarytm o podstawie 10
i potem z wlasnosci logarytmu
log a
k = k log a
i mam
log
10 √x * log
10 x = log
10 100
log
10 √x * log
10 x = 2log
10 10
| | 2log10 10 | |
log10 x = |
| |
| | log10 √x | |
log
10 x = 2 * log
√x 10
23 gru 20:52
Jack: dalej idąc...
podstawiam k =
√x
| | 2 | |
2 log10 k = |
| // : 2 |
| | log10 k | |
(log
10 k)
2 = 1
czyli
(log
10 k)= 1 lub (log
10 k) = − 1
czyli
podstaiwam
czyli
23 gru 20:58
Jack: Zgaduje ze wynikiem powinno byc tylko 100 ?

23 gru 21:01
5-latek: | | 1 | |
i |
| tez (przecież tez jest >0 |
| | 100 | |
23 gru 21:34
Jack: no ja tam nie wiem : D
23 gru 21:35
5-latek: No to podstaw rozwiązania do równania wyjsciowegi i sprawdz
23 gru 21:37
Jack: ta , zgadza sie w teorii : D
a założenie...
x ≥ 0
oraz
xlog podstawa 10 z pierwiastek x ≥ 0
23 gru 21:42
Jack:
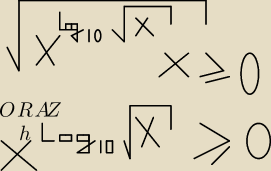
23 gru 21:46
zombi: √xlog √x = 10 /
2
x
log √x = 100 / log()
log
√x * logx = log100
log
2x = 4
| | 1 | |
logx = −2 lub logx = 2 ⇔ x= |
| lub x=100 |
| | 100 | |
23 gru 21:51
Jack: wlasciwie ile to jest :
(log x)2 ?
log2 x2 czy log2 x ?
23 gru 21:56
5-latek: log2x
a to możesz tez rozpisać jako logx*logx
23 gru 21:58
5-latek: Powiedz mi Jack czy to maja być trudne zadania ? (bo ja nie wiem )
Jeśli tak to mogę CI pare jeszcze znaleźć .
23 gru 22:00
Jack: nie dobra, starczy mi ...
i tak sie przemeczam, matmy az tak nie lubie, a kuje specjalnie zeby ogarnac ladnie maturke...
i dlatego tez rozwiazuje zadanka na tym forum...
ostatnio liczylem kilka calek (jeszcze ich nie mialem), wiec na razie mam dosc nauki ; )
co za duzo to nie zdrowo...swieta sa ; D
pora pograc w cos/ film obejrzec
23 gru 22:02
5-latek: Popieram

23 gru 22:09
5-latek: No to jak trochę ochlonales to teraz się popatrz na swój post 21:46
Rownanie możesz rozwiazac metoda starożytnych (tez )
Ale zauważ z eliczba logarytmowana musi być >0 ( w tym przypadku ta liczba jest √x
Wiec w tym przypadku x musi być >0 a nie x≥0 bo przecież logarytm z 0 nie istnieje
log10√0= Ile ? czyli jakie musi być x ?
23 gru 22:21
Jack: no ja rozumiem, ze liczba logarytmowana musi byc wieksza od zera...
ale to ze iks jest do potegi logarytm ... , to cos zmienia?
23 gru 22:27
25 gru 21:01
Jack: 4 >
3√36
3√64 >
3√36
c.n.u...
chyba ; D
25 gru 21:13
Eta:
ok

Można też tak : 3log
64>2 ⇒ log
664 > log
636 ⇒ 64>36
.........
25 gru 22:12

 Eta dobrze idzie mi jak narazie?
Eta dobrze idzie mi jak narazie? 

 Rozumiem ze to oto chodzi...o ile to mozna nazwac trapezem, ale zapewne tak skoro ma jedna pare
bokow rownoleglych
Rozumiem ze to oto chodzi...o ile to mozna nazwac trapezem, ale zapewne tak skoro ma jedna pare
bokow rownoleglych


 Jaka jest definicja trapezu ? ; o
Jaka jest definicja trapezu ? ; o



 Wskazówka na rys ( powinien wystarczyć
Dodaj teraz odpowiednie komentarze
Wskazówka na rys ( powinien wystarczyć
Dodaj teraz odpowiednie komentarze

 http://www.tomaszgrebski.pl/downloads/2015%20czerwiec%20PR%20klasa%20I%20grupa%20A.pdf
http://www.tomaszgrebski.pl/downloads/2015%20czerwiec%20PR%20klasa%20I%20grupa%20A.pdf


 https://matematykaszkolna.pl/forum/297327.html
wpis z 31 lipca 18: 30
https://matematykaszkolna.pl/forum/297327.html
wpis z 31 lipca 18: 30

 Robię zad 11 z tego linku (Post: 00;22)
Robię zad 11 z tego linku (Post: 00;22)


 https://matematykaszkolna.pl/forum/310415.html
Mialem tu napisac,a przypadkiem napisalem tam, sorki : D
https://matematykaszkolna.pl/forum/310415.html
Mialem tu napisac,a przypadkiem napisalem tam, sorki : D




 Czy moge ulozyc proporcje
Czy moge ulozyc proporcje


 Przed chwila "obczailem", ze jak mamy dwusieczna
to mamy taka rownosc...
Przed chwila "obczailem", ze jak mamy dwusieczna
to mamy taka rownosc...
 ewentualnie kątami...
ewentualnie kątami...
 ΔADC równoramienny i ΔDBC −− równoramienny i podobne z cechy (kkk)
to:
ΔADC równoramienny i ΔDBC −− równoramienny i podobne z cechy (kkk)
to:








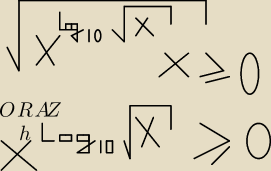

 Można też tak : 3log64>2 ⇒ log664 > log636 ⇒ 64>36
.........
Można też tak : 3log64>2 ⇒ log664 > log636 ⇒ 64>36
.........