nierownosci z pierw
logarytmy: Witam. Zacznę od pytania. Czy w nierównościach z pierwiastkiem zawsze mogę zacząć od
podniesienia obu stron do kwadratu, czy muszą być spełnione jakieś warunki? Jak np. tutaj.
√x−2 < 8 − x
Muszą być spełnione warunki jakieś czy walę kwadrat obu stron?
22 gru 21:02
wmboczek: warunki na istnienie pierwiastka i na nieujemną prawą stronę
22 gru 21:27
22 gru 21:28
Jack: o kurcze...przepraszam, nie tutaj
22 gru 21:28
Eta:
Pomyliłeś posty
22 gru 21:29
Jack: w zad 10 wyszlo mi, ze
x= 354
22 gru 21:30
Eta:
Nie wiem , nie liczyłam ( a odpowiedzi nie mam )
22 gru 21:31
logarytmy: Dlaczego prawa strona miała być nieujemna?
22 gru 22:04
MichałTH: a skąd będziesz wiedział jaki ma być znak nierówności?
22 gru 22:05
logarytmy: Nie rozumiem trochę... a > b, a,b ∊ R, To jakie muszą być spełnione warunki przy podniesieniu
do kwadratu?
22 gru 22:06
Eta:
−2<1 prawda?
no to po podniesieniu do kwadratu :
4 <1 ? prawda?
22 gru 22:08
logarytmy:
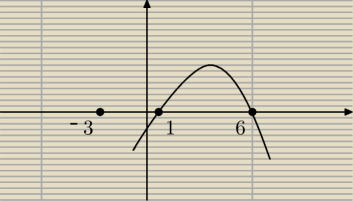
Skrajnie nie rozumiem jak psotawić przejrzyste na to warunki...
np.
√x+3 > x−3
D: x>−3
x+3 > x
2 − 6x + 9
−x
2 + 7x − 6 > 0
x
1 = 1
x
2= 6
a<0, więc ramiona do dołu
wg. wykresu x>0, dla x∊ (1;6), a w odp. jest (−3;6)
22 gru 22:15
Eta:
√x−2<8−x
założenia : x−2≥0 i 8−x≥0 ⇒ x∊<2,8>
przy takim założeniu możemy obustronnie podnieść nierówność do kwadratu
otrzymując : x−2< (8−x)2 ⇒ ........ (x−6)(x−11) >0 i x∊<2,8>
odp: x∊<2,6)
22 gru 22:16
logarytmy: Rzucisz Eta okiem na powyższe, proszę?
22 gru 22:22
Eta:
Odp: x∊( 3,6)
22 gru 22:25
logarytmy: −3;6.
22 gru 22:26
Eta:
√x+3>x−3
założenia : x+3≥0 i x−3≥0 ⇒ x≥ 3
teraz obustronnie do kwadratu:
x+3< x2−6x+9 ⇒ ( x−1)(x−6) <0 i x≥3 ⇒ x∊( 1,6) i x≥3
odp x∊<3,6)
22 gru 22:30
logarytmy: Wątpię, aby w Pazdrze były błędy..
22 gru 22:36
fds: 52
22 gru 22:51
Mila:
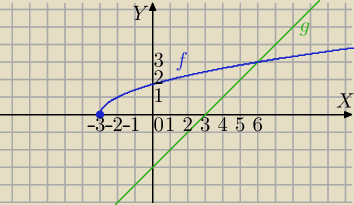√x+3>x−3
f(x)=
√x+3
g(x)=x−3
f(x)>g(x) dla x∊(−3,6)
Rozw. algebraiczne
D=<−3,
∞)
Lewa strona ≥0 dla x∊D
Prawa strona : x−3≥0 ⇔x≥3
Dla x∊<−3,3) wyrażenie : x−3<0 zatem
√x+3> x−3 dla każdego x∊<−3,3)
lub
Dla x≥3 obie strony nierówności są nieujemne
√x+3>x−3 /
2
x+3>x
2−6x+9
x
2−7x+6<0
Δ=25
x=1 lub x=6
x∊(1,6) i x≥3 ⇔x≥3
−−−−−−−−−−−−−−−−−−−−−−−−
odp. x∊<−3,6)
22 gru 23:36
Eta:
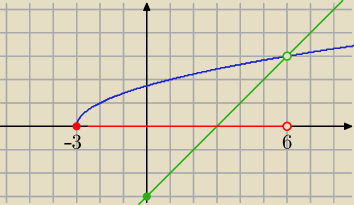
Faktycznie
Odp:
x∊<−3, 6)
Gdzie mam błąd w metodzie algebraicznej ?
22 gru 23:38
Eta:
Dzięki
Mila
Echh nie rozpatrzyłam przypadków ( żyję już świętami
22 gru 23:40
Mila:
Zdrowie dopisuje?
22 gru 23:44
Eta:
Tak, już wszystko ok
22 gru 23:49
Mila:
Eto, mam prośbę. Jeśli będziesz miała ochotę i czas , to przelicz zadanie z tym
czworościanem,
| | √6 | |
mam wynik |
| , i nie wiem, czy wszystkie ograniczenia uwzględniłam. |
| | 2 | |
Zadanie dość nietypowe. Nie pisz rozw., bo autor już zniknął, a myślę,
że to jakieś konkursowe zadanie.
22 gru 23:49
Eta:
Podeślij linka z tym zadaniem
22 gru 23:50
22 gru 23:52
22 gru 23:52
Mila:
Tak, właśnie to jest to zadanie.
22 gru 23:54
Mila:
Nie licz dzisiaj, bo jest trochę rachunków.
22 gru 23:54
23 gru 00:03
Mila:
Dziękuję bardzo
23 gru 00:08
Kacper:
Patrzę na zadanko.
23 gru 11:42