Geometria analityczna
Ania: Prosta o równaniu x−2y+2=0 przecina okrąg o: x2 +y2 −6x −16=0 w punktach A i B.
a)wyznacz równanie ogólne symetralnej m cięciwy AB
b)wyznacz współrzędne takiego punktu M∊m, dla którego trójkąt ABM jest prostokątny.
Bardzo proszę o pomoc jak to się robi po kolei . Nie wiem w ogóle jak to zrobić.
29 lis 10:15
sushi_gg6397228:
1. uklad rownan aby policzyć A i B
29 lis 10:21
Ania: x2 +y2 −6x−16=0
x=2y−2
(2y−2)2 +y2−6(2y−2)−16=0
4y2 −8y+4 +y2 −12y+12−16=0
5y2 −20y +0
29 lis 10:46
Ania: i jak dalej?
29 lis 10:46
sushi_gg6397228:
=0
Δ y1, y2
29 lis 10:53
Ania:
y1=0
y2=4
29 lis 10:57
sushi_gg6397228:
masz y1, to policz x1 , to samo dla x2
29 lis 10:58
Ania:
dla y1=0 x1=−2
dla y2=4 x2=6
29 lis 11:02
sushi_gg6397228:
Niech A=(−2; 0), B= (6;4)
a) jaki masz pomysł na to?
29 lis 11:04
misiak:
ALBO INNĄ METODĄ:
wyznaczyć równanie prostej prostopadłej do danej,
przechodzącej przez środek okręgu

29 lis 11:05
Ania: obliczyć współczynnik a i podstawić do równania prostej y=ax+b ?
29 lis 11:11
sushi_gg6397228:
jakie "a " i jakiej prostej?
29 lis 11:12
Ania: to nie tak ?
29 lis 11:14
sushi_gg6397228:
trzeba nazywać proste po imieniu
tutaj mozna policzyć dwie proste, a Twój wpis o 11.11 oznacza, że nie wiesz o co chodzi
29 lis 11:15
Ania: ja tego nie rozumiem

29 lis 11:18
sushi_gg6397228:
równanie ogólne symetralnej m cięciwy AB −−> co to oznacza, jak to rozumiesz
29 lis 11:19
5-latek: A wiesz co to jest symetralna ?
29 lis 11:19
Ania: trzeba obliczyć S?
29 lis 11:24
sushi_gg6397228:
brak odpowiedzi na posty o 11.19
znowu rzuciłaś " S" i mamy zgadywać co masz na myśli
29 lis 11:27
Ania: S− prosta prostopadła do danego odcinka. to wiem
29 lis 11:29
sushi_gg6397228:
dla mnie S oznaczał środek odcinka AB
nazwy prostych daje sie małą literką
29 lis 11:30
Ania: jej wzór to: xa+bb/2 ,ya+yb/2
29 lis 11:30
misiak:
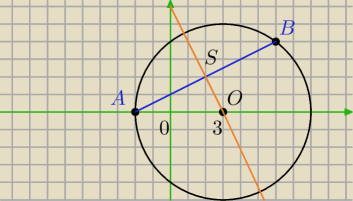
29 lis 11:30
Ania: to ja już się pogubiłam
29 lis 11:31
sushi_gg6397228:
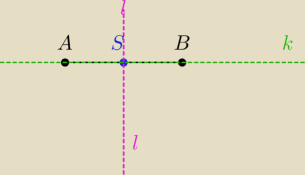
mozesz tak
1. znaleźć środek odcinka AB−−> punkt S
2. wyznaczyć prostą
k
3. znając "a" prostej k znaleźć współ. "a" dla prostej " l "
4. wyznaczyć prostą l przechodzącą przez S i potem zapisać w postaci Ax + By+C=0 ( ogólnej)
lub post 11.05
1. wyznaczyć środek okręgu − punkt O
2. wyznaczyć prostą
k
3. znając "a" prostej k znaleźć współ. "a" dla prostej " l "
4. wyznaczyć prostą l przechodzącą przez O i potem zapisać w postaci Ax + By+C=0 ( ogólnej)
29 lis 11:35
Ania: punkt S(2,2)
jak obliczyć k?
29 lis 11:37
sushi_gg6397228:
1 sposób: wzór na prostą przechodzacą przez dwa punkty ( tablice maturalne)
2 sposób:
y=ax+b i układ równan ( podstawiasz współrzędne punktów A i B)
29 lis 11:39
Ania: a=2
29 lis 11:41
29 lis 11:42
misiak:
przecież równanie prostej "k" było dane
29 lis 11:48
Ania: wyszło mi,że y = 12x +1
29 lis 11:48
Ania: to ja już nie wiem
29 lis 11:49
misiak:
dobrze ci wyszło

29 lis 11:51
Ania: i co dalej mam zrobić?
29 lis 11:51
misiak: masz już prostą :"k"
29 lis 11:51
Ania: tak
29 lis 11:52
misiak:
przejść do punktu 3. i 4. pierwszego sposobu
29 lis 11:52
Ania: współczynnikiem z będzie 12 ?
29 lis 11:53
Ania: a
29 lis 11:53
misiak:
tak...a teraz współczynnik dla prostpoadłej
29 lis 11:54
Ania: jak go znaleźć ?
29 lis 11:55
29 lis 11:56
Ania: skąd wezmę a2?
29 lis 11:59
Ania: a2=−2
29 lis 12:02
29 lis 12:03
29 lis 12:03
Ania: czyli a2=2
29 lis 12:04
misiak:
zgadza się ...a2=−2
29 lis 12:04
Ania: czyli a
2=−2

29 lis 12:04
Ania: mam już te współczynniki. Co następnie robię?
29 lis 12:04
misiak:
teraz l: y=a2x+b2 i punkt S=(2,2)
29 lis 12:05
Ania: czyli 2=−2*2+b2
b2=12
29 lis 12:07
misiak: dobrze policz b2.....popatrz na wykresie
w którym punkcie prosta l przecina oś Oy
29 lis 12:09
Ania: w punkcie S przecina
29 lis 12:10
misiak:
popatrz na mój rysunek....11.30
29 lis 12:11
misiak:
pomyliłaś się w rachunkach licząc b2...
a obliczona liczba powinna być widoczna na osi Oy
29 lis 12:12
Ania: y=6
29 lis 12:12
Ania: czy mógłbyś mi napisać jak to będzie?
29 lis 12:15
Ania: W odpowiedziach mam, że:
a) m:2x+y−6=0
b)M1(0,6) lub M2(4,−2)
29 lis 12:17
misiak:
dokończ obliczenia: 2=−2*2+b2
2=−4+b2
b2=.....
29 lis 12:36
Ania: b
2=6

29 lis 12:36
misiak:
czyli l: y=....
29 lis 12:37
misiak:
potem wszystko na lewą stronę i masz odpowiedź do a)
29 lis 12:38
Ania: −2x+6=y
29 lis 12:38
Ania: y+2x−6=0
29 lis 12:39
misiak:
y=−2x+6
2x+y−6=0
29 lis 12:39
misiak: ok

29 lis 12:40
Ania: jak wyznaczyć teraz współrzędne punkty M?
29 lis 12:41
29 lis 12:49
Ania: jak mam znaleźć x?
29 lis 12:51
Ania: proszę, niech ktoś napisze mi to do końca jak zrobić ze szczegółami
29 lis 13:33
Jack: misiak − 12:49
dał Ci wzór
29 lis 13:34
Ania: nie wiem jak to zrobić
29 lis 13:36
Ania: :(
29 lis 13:36
Jack: napisz równania i punkty które już znasz
29 lis 13:36
Ania: Punkt;
A (−2,0)
B(6,4)
S(2,2)
29 lis 13:39
Ania: Prosta:
k:y=12x +1
l:y+2x−6=0
29 lis 13:40
misiak:
A=(−2,0) B=(4,6) M=(x,−2x+6)
|AM|=√(xM−xA)2+(yM−yA)2
|AM|=√(x+2)2+(−2x+6)2
|BM|=√(x−4)2+(−2x+6−6)2
|AB|=√(4+2)2+62=√72=6√2
|AM|2+|BM|2=|AB|2
(x+2)2+(−2x+6)2+(x−4)2+(−2x)2=72
dokończ
29 lis 13:41
Ania: dobrze
29 lis 13:42
misiak: poprawka: będzie trochę inaczej
A=(−2,0) c[B=(6,4)] M=(x,−2x+6)
29 lis 13:47
Jack: B=(6,4) zamiast B=(4,6)
Dokładnie tak misiak

29 lis 13:50
misiak: A=(−2,0) B=(6,4) M=(x,−2x+6)
|AM|=√(x+2)2+(−2x+6)2
|BM|=√(x−6)2+(−2x+6−4)2
|AB|=√(6+2)2+42=√80
29 lis 13:50
Ania: czyli w |AB| jak będzie?
29 lis 13:50
Ania: okey

29 lis 13:50
misiak:
(x+2)2+(−2x+6)2+(x−6)2+(−2x+2)2=80
29 lis 13:52
misiak: powinno być dobrze
29 lis 13:52
Ania: wyszło mi 10x2+24x=0
teraz muszę obliczyć deltę i koniec?
29 lis 13:59
misiak:
10x2−40x=0
x(x−4)=0
x=0 lub x−4=0
x=4
29 lis 14:02
misiak: M=(x, −2x+6)
M1=.... M2=.....
29 lis 14:03
Ania: Dziękuję Tobie bardzo

29 lis 14:05
Ania: wyszło tak jak powinno

29 lis 14:05
misiak: 
29 lis 14:06
Ania: 
29 lis 14:06



 mozesz tak
1. znaleźć środek odcinka AB−−> punkt S
2. wyznaczyć prostą k
3. znając "a" prostej k znaleźć współ. "a" dla prostej " l "
4. wyznaczyć prostą l przechodzącą przez S i potem zapisać w postaci Ax + By+C=0 ( ogólnej)
lub post 11.05
1. wyznaczyć środek okręgu − punkt O
2. wyznaczyć prostą k
3. znając "a" prostej k znaleźć współ. "a" dla prostej " l "
4. wyznaczyć prostą l przechodzącą przez O i potem zapisać w postaci Ax + By+C=0 ( ogólnej)
mozesz tak
1. znaleźć środek odcinka AB−−> punkt S
2. wyznaczyć prostą k
3. znając "a" prostej k znaleźć współ. "a" dla prostej " l "
4. wyznaczyć prostą l przechodzącą przez S i potem zapisać w postaci Ax + By+C=0 ( ogólnej)
lub post 11.05
1. wyznaczyć środek okręgu − punkt O
2. wyznaczyć prostą k
3. znając "a" prostej k znaleźć współ. "a" dla prostej " l "
4. wyznaczyć prostą l przechodzącą przez O i potem zapisać w postaci Ax + By+C=0 ( ogólnej)









