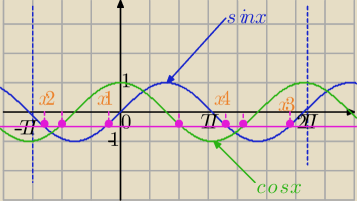
funkcje sinx oraz cosx Aśka: We wspolnym ukladzie wspolrzednych naszkicuj wykresy funkcji f(x)=sinx oraz g(x)=cosx dla x ∊ <−π,2π> wyznacz wartosci funkcji f dla tych argumentow, dla ktorych funkcja g przyjmuje wartosc rowna

	1
−
	2

5-latek: https://matematykaszkolna.pl/forum/294873.html poczytaj to sobie

5-latek: https://matematykaszkolna.pl/forum/294865.html to także

Aśka: Probowalam wiele razy zrobic to zadanie ale wynik nie zgadza mi sie z odpowiedziami g(x)=−0,5 dla x∊{−0,75π,0,75π,1,25π} f(−0,75π)=−0,5 f(0,75π)=0,5 f(1,25π)=−0,5 Tak mi wyszlo a w odpowiedziach jest

	2π		−√3
f(−		)=
	3		2

	2π		√3
f(		)=
	3		2

	4π		−√3
f(		)=
	3		2

Aśka: dlaczego cos0,5=π/3

Aśka: nie rozumiem

Qulka: cos π/3 = 0,5

Aśka: Ja juz nic nie wiem O co chodzi w tych zadaniach o co chodzi w moim zadaniu i jak sie rysuje wykres cos x ? bo na moim wykresie nic sie nie zgadza

Aśka: Pogubilam sie

Qulka: https://matematykaszkolna.pl/strona/427.html

Qulka: https://matematykaszkolna.pl/strona/1583.html

Aśka: okej okej juz to chyba widze dzieki jak bd jeszcze miala jakies watpliwosci to napisze a na razie dzieki za pomoc

Mila:

	1
y=−
	2

	1
sinx=		dla tego równania masz serię rozwiązań
	2

	π		5π
x=		+2kπ lub x=		+2kπ
	6		6

korzystając z tego ustalasz rozwiązania dla równania

	1
sinx=−		np. tak
	2

	π		5π
x=−		+2kπ lub x=−		+2kπ
	6		6

dla k=0 masz

	π		5π
x1=−		lub x2=−
	6		6

dla k=1 masz

	11π		7π
x3=		lub x4=
	6		6

dla k=2 będą poza przedziałem (−π,2π) Spróbuj zrobić tak samo z cosinusem.

Aśka: juz rozumiem jak to robic dziekuje za pomoc jeszcze raz

Mila: