| 1 | ||
sinx= | ||
| 2 |
| π | 5π | |||
x= | + 2kπ v x= | + 2kπ | ||
| 6 | 6 |
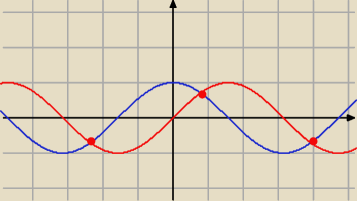 sin x = cos x
sin x = cos x
| π | ||
x = | + π*k , k − dowolna liczba całkowita | |
| 4 |
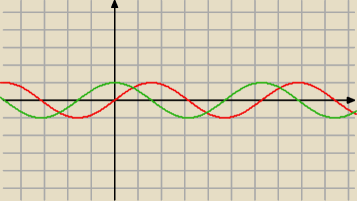 y=sinx czerwony
y=cosx zielony
przecież wiesz ze sinx = cosx dla kąta 45 stopni i uwzglednij okresowość tych funkcji
y=sinx czerwony
y=cosx zielony
przecież wiesz ze sinx = cosx dla kąta 45 stopni i uwzglednij okresowość tych funkcji
| π | ||
sinx=cosx /: cosx ( możesz podzielić, bo | nie spełnia równania, zatem cosx≠0) | |
| 2 |
| sinx | |
=1⇔ | |
| cosx |
| π | ||
x= | +kπ | |
| 4 |
| π | ||
sinx−sin( | −x)=0 | |
| 2 |
|
| |||||||||||||||||||||
2*cos | *sin | =0⇔ | ||||||||||||||||||||
| 2 | 2 |
| π | π | |||
2*cos | *sin(x− | )=0⇔ | ||
| 4 | 4 |
| π | ||
sin(x− | )=0 | |
| 4 |
| π | ||
x− | =kπ⇔ | |
| 4 |
| π | ||
x= | +kπ | |
| 4 |
| π | π | π | ||||
cos( | − x) = cosx ⇒ | − x = x + k*2π lub | − x = −x + k*2π sprzeczność | |||
| 2 | 2 | 2 |
| π | π | |||
2x = | − k*2π ⇒ x = | − k*π | ||
| 2 | 4 |
| α−β | α+β | |||
We wzorze jest sinα − sinβ= 2sin | cos | |||
| 2 | 2 |


| π | ||
ctgx=ctg | ||
| 4 |
| π | ||
x= | +kπ | |
| 4 |
| π | ||
Korzystając ze wzoru sin x = cos( | −x) oraz poniższej regułki: | |
| 2 |
| π | ||
cos( | −x) = cos x | |
| 2 |
| π | π | ||
−x = x + 2k*π lub | −x = −x + 2k*π | ||
| 2 | 2 |
| π | π | |||
z pierwszego x = | + k*π, drugie to sprzeczność bo | = 2k*π to sprzeczne równanie | ||
| 4 | 2 |
| π | ||
Zostaje x = | + k*π | |
| 4 |